Logistic Regression详解

Regression是什么？

• Regression：找到一个模型去表示数据间的关系
• Linear Regression：使用线性模型拟合数据
• Logistic Regression：其实本质也是线性拟合，但引入了log，这个之后会详细说

也就是说，不管什么Regression，都是想找到一个模型来拟合数据。

Likelihood

Likelihood与我们平常所说的Probability相反。

举个例子，平常说B站有60%的人是宅男，这个60%就是概率。我们换个思路，如果告诉你一个人是宅男，那他有多大的可能是B站用户呢？我们同意“宅男都混B站”这个判断的话，就说这个宅男100%是B站用户。这里100%就是likelihood。

其实到这里，我们已经完成了一次预测 —— 预测一个宅男是否为B站用户。事实上，这个在现实生活中非常有用。比如根据症状判断是否得了癌症，根据性别年龄等特征判断是否已婚等等。

regression的主要用途就是根据输入的特征做判断，并使本系统的判断与实际输出之间的差值最小。

Logistic Regression

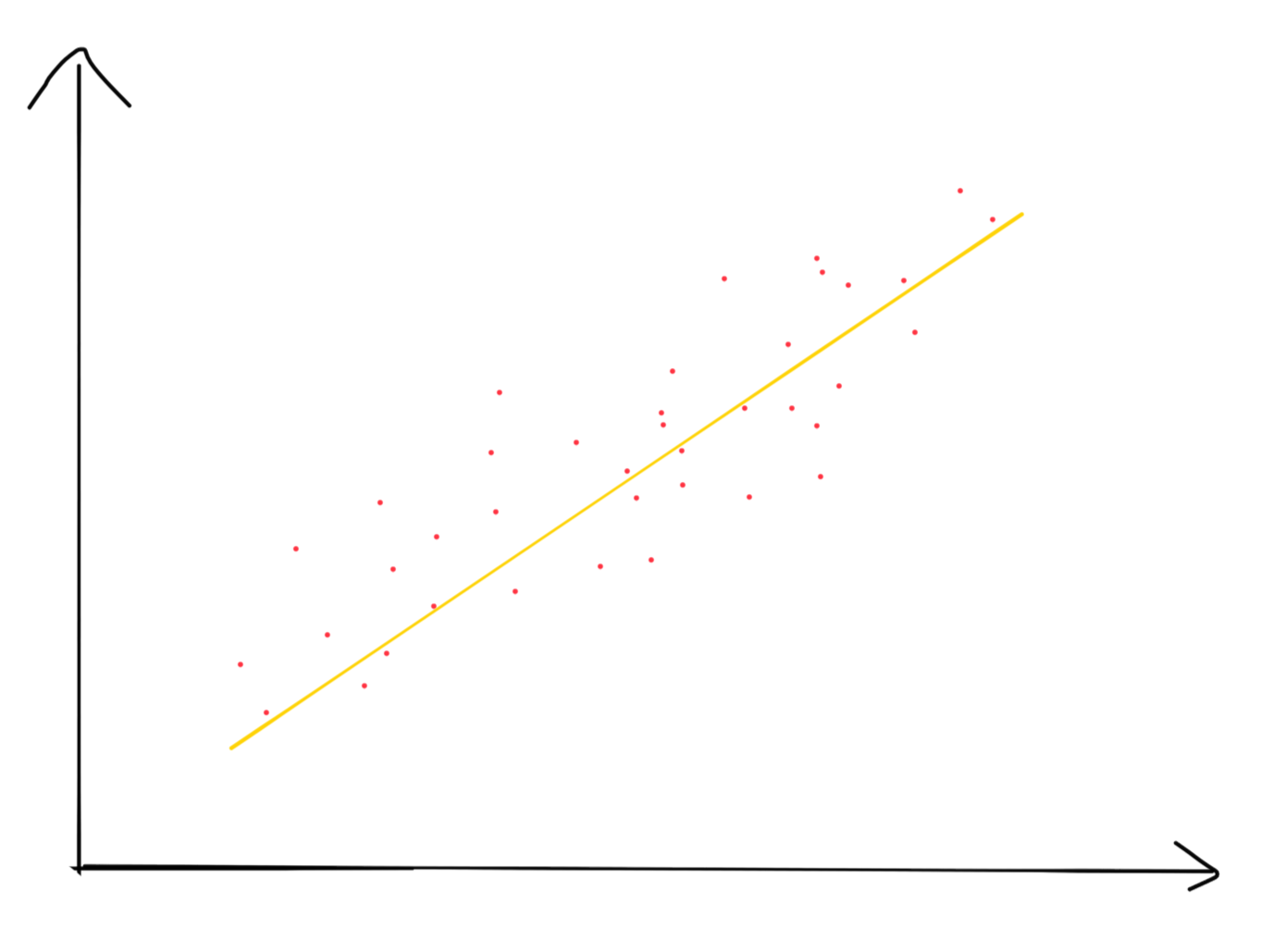
引子：我们常用的是线性拟合，为什么？当然因为线性拟合简单，比如下面的红色数据点，我们可以简单的拿一个线性模型拟合（黄线）

可是，如果我们的点不是这么的符合线性条件呢？

使用最大后验概率作为模型质量的评测方式，我们需要使输入的已知点的likelihood最大，从而得到一个比较好的模型。

假设y的取值为1或0（也就是说，所有数据分为两类）

后验概率：

假设

$$P（Y＝1|X＝x）＝P（x；\theta）$$
（给定输入x，输出为1的概率）

可以得到，

∏i=1mP（Y＝yi|X＝xi）＝∏i=1mP（xi；θ）yi(1−P（xi；θ）)