PCA算法（主成分分析）

写在前面

Principle Component Analysis 顾名思义，是通过分析向量空间的主成分，将主成分提取出来，不重要的成分略去，从而达到降维压缩信息的目的。

那什么才是主成分呢？大家应该知道，一个空间会有自己的一组基向量，空间中的任何一个向量都可以通过基向量的组合来表示。

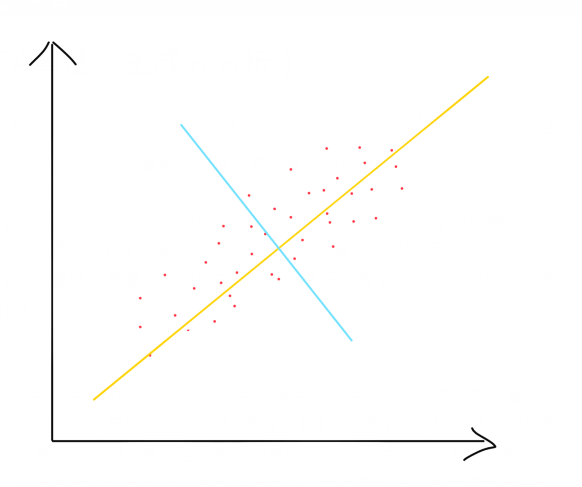
举个栗子，假如我们有一组2维的点，那么我们可以找到2个基向量，让这一组点对着这2个基向量进行投影。每个基向量上，投影后的点越分散，这个基向量就越重要。也就是主成分。不明白的看下图。（原谅我的灵魂画作）

红色的点就是已有的一组2维点，黄色和蓝色的线代表两个基向量的方向。如果我们要把红色的点从2维降到1维，向哪个方向投影才能保存更多的信息呢？直观上看，当然是黄向量比较好，红点在黄线上的投影很分散，而在蓝线上的投影很多会重叠在一起。黄向量就是比蓝向量更主要的成分。

好了，我们现在知道什么是主成分了，那怎么才能把它提取出来呢？一般是通过对红点各维的协方差矩阵进行特征分解，选取最大的几个特征值对应的特征向量，组成低维空间的一组基向量。再将原始的红点投影到这组低维基向量上，就得到了红点降维后的坐标。这中间涉及到一些数学的计算和解释，就放在下面了。

投影

向量的内积相当于投影，

 A * B = |A||B|cos(a)

|B|=1时，

 A * B= |A|cos(a)

此时，A和B的内积相当于A向B方向投影的长度。

另外，当新基的原点与原基的原点不同时，要先进行变换使原点重合。

讨论二维空间基变换

在我们常用的笛卡尔坐标系中，一点(x,y)可以分解为

 x = r * cos(θ)   y = r * sin(θ)

相当于把向量(x,y)投影到两个基向量上，

 (1,0) 和 (0,1)

x和y相当于投影后的长度。

一个向量的准确描述需要给出一组基，以及向量在各个基方向上的投影长度。

注意：不管变换什么样的基向量，向量相对于原点的位置是不变的。

例：将基本基上的坐标(3,2)变换为基(1/√2,1/√2)、(-1/√2,(1/√2))的坐标。
（注意，新基的坐标是在基本基上确定的）

⎛⎝⎜⎜⎜12√−1