漫步凸分析三——凸集代数

有许多种代数运算可以保留凸性。

例如，如果$C$是$R^n$中的凸集，那么所有平移操作$C+a$和标量乘法$\lambda C$同样是凸集，其中

$$\lambda C=\{\lambda x|x\in C\}$$

从几何上看，如果$\lambda>0$，那么$\lambda C$就是$C$伸缩$\lambda$倍得到的图像。

过原点$C$的对称反射是$-C=(-1)C$，对于凸集$C$，如果$-C=C$，我们就说这个凸集是对称的。这样的凸集(如果非空)一定包含原点，因为它除了包含每个向量$x$和$-x$外，还包含$x$与$-x$之间的线段。对称的非空凸锥是子空间(定理2.7)。

定理3.1 如果$C_1,C_2$是$R^n$中的凸集，那么他们的和$C_1+C_2$依然是凸集，其中

$$C_1+C_2=\{x_1+x_2|x_1\in C_1,x_2\in C_2\}$$

证明：令$x,y$是$C_1+C_2$中的点，那么存在$x_1,y_1\in C_1,x_2,y_2\in C_2$使得

$$x=x_1+x_2,\quad y=y_1+y_2$$

对于$0<\lambda<1$，我们有

$$(1-\lambda)x+\lambda y=[(1-\lambda)x_1+\lambda y_1]+[(1-\lambda)x_2+\lambda y_2]$$

然后利用$C_1,C_2$的凸性

$$(1-\lambda)x_1+\lambda y_1\in C_1,\quad (1-\lambda)x_2+\lambda y_2\in C_2$$

可以得出$(1-\lambda)x+\lambda y$属于$C_1+C_2$。$||$

我们举例说明，如果$C_1$是任意凸集，$C_2$是非负象限，那么

$$\begin{align*} C_1+C_2 &=\{x_1+x_2|x_1\in C_1,x_2\geq0\}\\ &=\{x|\exists x_1\in C_1,x_1\leq x\} \end{align*}$$

根据定理3.1，当$C_1$是凸集时，后面的集合是凸的。

根据定义，集合$C$为凸意味着

$$(1-\lambda)C+\lambda C\subset C,\quad 0<\lambda<1$$

我们一会儿会看到，对于凸集而言等式的情况也是成立的。一个集合$K$，当且仅当对于所有$\lambda>0$时，$\lambda K\subset K$恒成立，那么这个集合就是凸锥，并且$K+K\subset K$(定理2.6)。

如果$C_1,\ldots,C_m$是凸集，那么下面的线性组合也是凸集

$$C=\lambda_1C_1+\cdots+\lambda_mC_m$$

自然得，当$\lambda_1\geq0,\ldots,\lambda_m\geq0$并且$\lambda_1+\cdots+\lambda_m=1$时，上面的线性组合$C$叫做$C_1,\ldots,C_m$的凸组合，从几何上讲，我们可以将$C$ 看成$C_1,\ldots,C_m$的某个混合物，例如，令$C_1,C_2$分别是$R^2$中的三角形和圆盘，当$\lambda$从0到1变化时

$$C=(1-\lambda)C_1+\lambda C-2$$

从三角形变到有圆角的三角形，圆的主导地位不断增加，最终变成一个圆盘。

为了几何上更加直观，有时可以将$C_1+C_2$看成所有平移$x_1+C_2$的并，其中$x_1$在$C_1$上变化。

对于集合的加法和标量乘法，哪些代数法则是有效的呢？简单老说，及时不是凸的，下面的法则都是成立的

$$\begin{align*} C_1+C_2 &=C_2+C_1\\ (C_1+C_2)+C_3 &=C_1+(C_2+C_3)\\ \lambda_1(\lambda_2C) &=(\lambda_1\lambda_2)C\\ \lambda(C_1+C_2) &=\lambda C_1+\lambda C_2 \end{align*}$$

只包含0的凸集是加法操作的恒等元素，如果集合包含的元素超过一个，那么加法逆是不存在的；通常我们可以说当$C\neq\emptyset$时，$0\in[C+(-C)]$

下面介绍的定理是集代数中依赖凸的一个重要法则，这个分配律满足实际上等价于集合$C$是凸的，因为这个法则暗含着$0\leq\lambda\leq1$时$\lambda C+(1-\lambda)C$含于$C$。

定理3.2 如果$C$是凸集并且$\lambda_1\geq0,\lambda_2\geq0$，那么

$$(\lambda_1+\lambda_2)C=\lambda_1C+\lambda_2C$$

证明：无论$C$是否为凸集，包含$\subset$都是成立的。从凸关系

$$C\supset(\lambda_1)/(\lambda_1+\lambda_2))C+(\lambda_2/(\lambda_1+\lambda_2))C$$

中我们可以得出反向包含成立，这里假设$\lambda_1+\lambda_2>0$，然后两边乘以$\lambda_1+\lambda_2$即可得出。如果$\lambda_1$或$\lambda_2$是0，定理明显成立。$||$

从这个定理我们可以得出当$C$是凸集时，$C+C=2C,C+C+C=3C$ 等等。

给定$R^n$中的两个凸集$C_1,C_2$，有唯一一个既含于$C_1$ 又含于$C_2$的最大凸集，即$C_1\cap C_2$，还有唯一一个即包含$C_1$又包含$C_2$的最小凸集，即$(C_1\cup C_2)$。这个结论不知限于一对集合，对于任意的$\{C_i,i\in I\}$结论都是成立的，换句话说，在包含的自然偏序下$R^n$中所有凸集就是完备格(complete lattice)。

定理3.3 令$\{C_i|i\in I\}$是$R^n$中任意凸集组成的集合，并且令$C$表示这个集合并的凸包，那么

$$C=\cup\{\Sigma_{i\in I}\lambda_i C_i\}$$

其中这个并包含所有有限的凸组合(即选择所有系数$\lambda_i$的非负值，使得只有有限个为非零并且相加为1)。

证明：根据定理2.3，$C$是所有凸组合$x=\mu_1y-1+\cdots+\mu_my_m$的集合，其中向量$y_1,\ldots,y_m$属于集合$C_i$的并。实际上，我们通过取系数为非零并且来自不同集合$C_i$的向量的组合就能得到$C$，因为那些系数为零的向量可以从组合中忽略掉，而且如果两个正系数的向量属于同一个集合$C_i$，用$y_1,y_2$表示，那么$\mu_1y_1+\mu_2y_2$可以用$\mu y$代替，其中$\mu=\mu_1+\mu_2$

$$y=(\mu_1/\mu)y_1+(\mu_2/\mu)y_2\in C_i$$

因此$C$就是形如

$$\mu_1C_{i_1}+\cdots+\mu_mC_{i_m}$$

有限凸组合的并，其中$i_1,\ldots,i_m$是不同的。除了符号不一样外，它和定理中描述的并是一样的。$||$

给定任意从$R^n$到$R^m$的线性变换$A$，习惯上我们定义

$$\begin{align*} AC &=\{Ax|x\in C\}\quad for\quad C\subset R^n\\ A^{-1}D &=\{x|Ax\in D\}\quad for\quad D\subset R^m \end{align*}$$

我们称$AC$为$A$下$C$的像(image)，$A^{-1}D$为$A$下$D$ 的原像(inverse image)，事实证明这个操作保留凸性。(注意线性变换的逆只有在单值映射时才存在，而这里的符号$A^{-1}D$跟它是不同的)

定理3.4 令$A$是从$R^n$到$R^m$的线性变换，那么对于$R^n$ 中的所有凸集$C$，$AC$是$R^m$中的凸集，对于$R^m$中的所有凸集$D$，$A^{-1}D$是$R^n$中的凸集。

推论3.4.1 凸集$C$在子空间$L$上的正交投影是一个凸集。

证明：映射到$L$上的正交投影是线性变换，它对每一个点$x$ 分配唯一的一个$y\in L$使得$(x-y)\perp L$。$||$

定理3.4中$A^{-1}D$为凸的一种解释是当$y$在一个凸集上变化时，联立线性方程组$Ax=y$的解$x$也会在一个凸集上变化，如果$D=K+a$，其中$K$是$R^n$中的非负象限，$a\in R^m$，那么$A^{-1}D$是向量$x$的集合，它使得$Ax\geq a$，即$R^n$中某个线性不等式组的解集。如果$C$是$R^n$中的非负象限，那么$AC$ 是向量$y\in R^m$的集合，它使得等式$Ax=y$ 有一个解$x\geq0$。

定理3.5 令$C,D$分别是$R^m,R^p$中的凸集，那么

$$C\oplus D=\{x={y,z}|y\in C,z\in D\}$$

是$R^{m+p}$的凸集。

定理3.5中的集合称为$C,D$的直和(direct sum)。对于平常的和$C+D$，其中$C\subset R^n,D\subset R^n$，如果每个向量$x\in C+D$可以唯一地表示成$x=y+z$ 的形式，其中$y\in C,z\in D$，那么我们也称它为直和。对于对称凸集$C-C,D-D$，当且仅当他们在$R^n$中的公共元素只有零向量时他们的和才是直和。(这就表明$R^n$可以表示成两个子空间的直和，一个包含$C$，另一个包含$D$)

定理3.6 令$C_1,C_2$是$R^{m+p}$的凸集，$C$是向量$x=(y,z)$的集合(其中$y\in R^m,z\in R^p$)使得存在向量$z_1,z_1$，他们满足$(y,z_1)\in C_1,(y,z_2)\in C_2,z_1+z_2=z$，那么$C$是$R^{m+p}$中的凸集。

证明：令$(y,z)\in C$，其中$z_1,z_2$如定理中所示，同样设$(y^{'},z^{'}),z_1^{'},z_2^{'}$，那么对于$0\leq\lambda\leq1$，$y^{''}=(1-\lambda)y+\lambda y^{'},z^{''}=(1-\lambda)z+\lambda z^{'}$，我们有

$$\begin{align*} (y^{''},(1-\lambda)z_1+\lambda z_1^{'}) &=(1-\lambda)(y,z_1)+\lambda(y^{'},z_1^{'})\in C_1\\ (y^{''},(1-\lambda)z_2+\lambda z_2^{'}) &=(1-\lambda)(y,z_2)+\lambda(y^{'},z_2^{'})\in C_2\\ z^{''}=(1-\lambda)(z_1&+z_2)+\lambda(z_1^{'}+z_2^{'})\\ =((1-\lambda)z_1&+\lambda z_1^{'}+(1-\lambda)z_2+\lambda z_2) \end{align*}$$

因此向量

$$(1-\lambda)(y,z)+\lambda(y^{'},z^{'})=(y^{''},z^{''})$$

属于$C$。$||$

注意到定理3.6描述的是$R^{m+p}$中凸集的某个交换(commutative)和结合(associative)运算，有无限多种方法在$R^n$ 上引入线性坐标系，然后相对于每个坐标系将每个向量表示成$y\in R^m,z\in R^p$，每种方式可以得到定理3.6 描述的运算(如果$R^n$分解成子空间直和的方式不同，那么运算就不同)，这种类型的运算称作部分加(partial addition)，平常的加法(即形如$C_1+C_2$的运算)可以看成定理3.6 中$m=0$ 的极端情况，而交(即形如$C_1\cap C_2$的运算)对应于$p=0$。 这两种极端情况之间有无限多种$R^n$中所有凸集类的部分和，每一个都是一种交换，结合二元运算。

刚刚提到的无限多种运算似乎非常随意，但是通过更特殊地考虑，我们可以列出四种运算做为自然运算。回忆一下，对于$R^n$中的每个凸集$C$，在$R^{n+1}$ 中有一个凸锥$K$包含原点并且有一个横截面是$C$，即由$\{(1,x)|x\in C\}$生成的凸锥，这个对应关系是一对一的。这类锥$K$由这样的凸锥组成，这些凸锥和半空间$\{(\lambda,x)|\lambda\leq0\}$只有唯一的公共点$(0,0)$。保留$R^{n+1}$中这类锥的运算对应于$R^n$中凸集的运算，$R^{n+1}$变成$(\lambda,x)$的分解操作可以将我们的注意力集中到$R^{n+1}$上的四种部分和运算，也就是只在$x$上进行加法运算，只在$\lambda$上进行加法运算，以及两种极端情况，即在$\lambda,x$上同时进行加法运算，同时都不进行加法运算。这四种运算明显保留了问题中的那类凸锥$K$。

现在让我们看看对于凸集而言部分和的四种运算意味着什么。假设$K_1,K_2$分别对应于凸集$C_1,C_2$，如果我们只对$K_1,K_2$上的$x$执行加法运算，当且仅当对于$(1,x_1)\in K_1,(1,x_2)\in K_2$，等式$x=x_1+x_2$恒成立时，$(1,x)$ 产生的$K$，因此对应于$K$的凸集是$C=C_1+C_2$。如果我们对两部分都执行部分和运算，当且仅当$(\lambda_1,x_1)\in K_1,(\lambda_2,x_2)\in K_2$，等式$x=x_1+x_2,1=\lambda_1+\lambda_2$恒成立时，$(1,x)$属于$K$，因此$C$是集合$\lambda_1C_1+\lambda_2C_2$的并，其中$\lambda_1\geq0,\lambda_2\geq0,\lambda_1+\lambda_2=1$，根据定理3.3我们知道，这实际就是conv$(C_1\cup C_2)$。$\lambda,x$上都不进行加法运算和$K_1,K_2$去交集是一样的，明显对应于形式$C_1\cap C_2$。剩下的那个运算就是只在$\lambda$上进行加法运算，当且仅当$(\lambda_1,x)\in K_1,(\lambda_2,x)\in K_2$时，其中$\lambda_1\geq0,\lambda_2\geq0,\lambda_1+\lambda_2=1$，$(1,x)\in K$，因此

$$\begin{align*} C &=\cup\{\lambda_1C_1\cap\lambda_2C_2|\lambda_i\geq0,\lambda_1+\lambda_2=1\}\\ &=\cup\{(1-\lambda)C_1\cap \lambda C_2|0\leq\lambda\leq1\} \end{align*}$$

我们用$C_1\#C_2$，运算$\#$叫做逆加法(inverse addition)。

定理3.7 如果$C_1,C_2$是$R^n$中的凸集，那么他们的逆和$C_1\#C_2$也是凸集。

逆和是$R^n$中所有凸集的一个交换，结合二元运算，它类似于平常的加法(可以用逐点运算来表示)，为了说明这个，我们首先注意到$C_1\#C_2$由所有形如

$$x=\lambda x_1=(1-\lambda)x_2,\quad 0\leq\lambda\leq1,\quad x_1\in C_1,\ x_2\in C_2$$

的向量$x$组成。这样的表达式需要$x_1,x_2,x$在同一条射线$\{\alpha e|\alpha>0\}$上，事实上，对于$\alpha_1\leq0,\alpha_2\leq0$，我们有$x_1=\alpha_1e,x_2=\alpha_2e$并且

$$x=[\alpha_1\alpha_2/(\alpha_1+\alpha_2)]e=(\alpha_1^{-1}+\alpha_2^{-1})^{-1}e$$

(如果$\alpha_1=0$或者$\alpha_2=0$，那么最后那个系数可能理解为0)，实际上这里的$x$只依赖与$x_1,x_2$，而不是$e$的选择。我们可能称它为$x_1,x_2$ 的逆和，用$x_1\#x_2$表示，向量的逆加法是交换和结合的扩展。

$$C_1\#C_2=\{x_1\#x_2|x_1\in C_1,x_2\in C_2\}$$

和$C_1+C_2$是并行的。

我们讨论的所有运算明显保留了$R^n$中所有凸锥，当然除了平移运算外。因此当$K_1,K_2,K$是凸锥时，集合$K_1+K_2,K_1\#K_2,\text{conv}(K_1\cup K_2),K_1\cap K_2,K_1\oplus K_2,AK,A^{-1}K,\lambda K$是凸锥，正标量乘法对锥来说是很平凡的运算：对于$\lambda>0$，我们有$\lambda K=K$，由于这个原因，在这种情况下，加法和逆加法基本简化为格运算。

定理3.8 如果$K_1,K_2$是包含原点的凸锥，那么

$$\begin{align*} K_1+K_2 &=\text{conv}(K_1\cup K_2)\\ K_1\#K_2 &=K_1\cap K_2 \end{align*}$$

证明：根据定理3.3，conv$(K_1\cup K_2)$是$(1-\lambda)K_1+\lambda K_2$的并，其中$\lambda\in[0,1]$，当$0<\lambda<1$时，后面那个集合变为$K_1+K_2$，当$\lambda=0$时变为$K_1$，$\lambda=1$时变为$K_2$。因为$0\in K_1,0\in K_2,K_1+K_2$既包含$K_1$又包含$K_2$，因此conv$(K_1\cup K_2)$和$K_1+K_2$是一致的。同样地，$K_1\#K_2$是$(\lambda K_1)\cap(1-\lambda)K_2$ 的交，其中$\lambda\in[0,1]$，当$0<\lambda<1$ 时，后面那个集合变成$K_1\cap K_2$，当$\lambda=0$或$\lambda=1$时$\{0\}\subset K_1\cap K_2$，因此$K_1\#K_2=K_1\cap K_2$。$||$

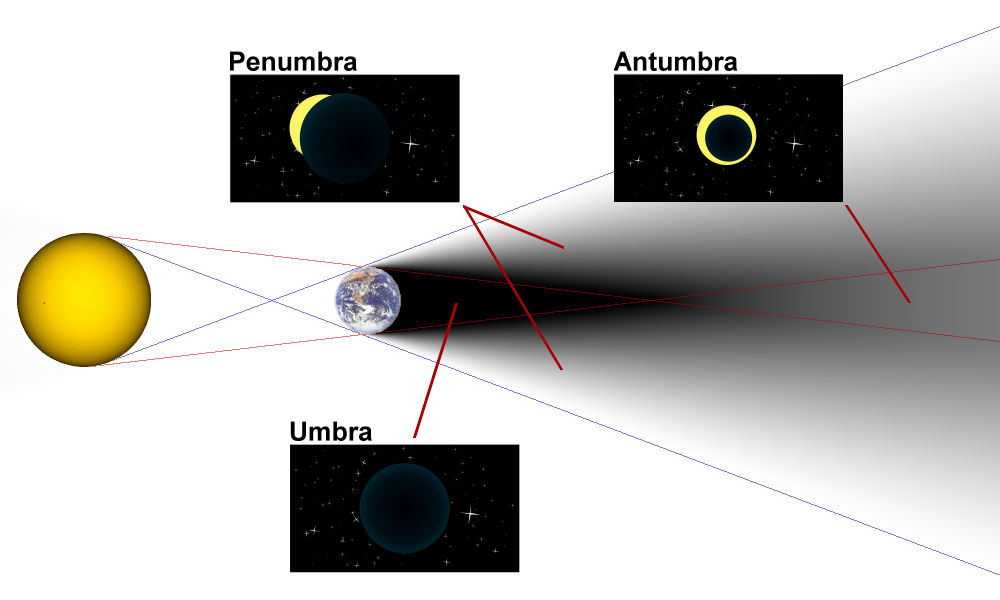
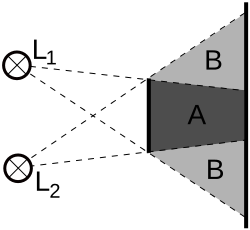
这里我们提出另一个很有趣的结构。给定$R^n$中两个不同的点$x,y$，半线$\{(1-\lambda)x+\lambda y|\lambda\geq1\}$ 可以看成光源在$x$处时$y$的阴影，而$y$在集合$C$上变化时得到半线的并就是$C$的阴影，这表明对于$R^n$中任意不相交的子集$C,S$，我们可以定义$C$相对于$S$的本影(umbra)为

$$\cap_{x\in S}\cup_{\lambda\geq1}\{(1-\lambda)x+\lambda C\}$$

$C$相对于$S$的半影(penumbra)为

$$\cup_{x\in S}\cup_{\lambda\geq1}\{(1-\lambda)x+\lambda C\}$$

如果$C$是凸的，那么本影就是凸的，如果$C,S$都是凸的，那么半影是凸的。

附：

本影(umbra):发光体（非点光源）所发出光线被非透明物体阻挡后，在屏幕（或其他物体）上所投射出来完全黑暗的区域。此处发光体的光线完全被物体阻挡，而没有任何光线到达。

半影(penumbra):天体本影周围有部分光通过的影区。呈圆锥形，顶端指向太阳。其边界同月球（或地球）、太阳相内切。在半影区内只能见到部分太阳。当月球半影扫过地球时，便发生日偏食。在影像上，半影是通过观察影像来认识物体的主要障碍，半影又称为模糊阴影。

图1

图2 本影(A)和半影(B)