线性判别分析(Linear Discriminant Analysis,LDA)

本文为学习总结，主要参考PRML[1]和cnblogs[2]上的那篇博客。

线性判别式分析，又称为Fisher线性判别。

二分类情况

假设有一个D维输入向量x，然后用下式投影到一维空间

$$y=w^Tx$$
对y设置一个阈值Thre，然后把y大于Thre的归为1类，把其余的归为2类这样就是得到一个标准的线性分类器。一般地，向一维投影会造成很多信息丢失，因此在原本D维空间能完美分离的样本可能在一维空间中互相重叠。但是，通过过调整权重向量 $w$，可以选择让类别之间区分最大的一个投影。在二分类情况下，设1类有$N_1$个点，2类有 $N_2$个点。两类的均值向量为：
$$m_1=\frac{1}{N_1}\sum_{n\in C_1}x_n,m_2=\frac{1}{N_2}\sum_{n\in C_2}x_n$$
如果投影w上，最简单的度量类别之间分开程度的方式就是类别均值向量投影之后的距离。可以选择w使式子 $m_2-m_1=w^T(m_2-m_1)$取得最大值（等号左边的是均值向量投影后的值），其中 $m_k=w^Tm_k$表示类别 $C_k$的投影数据的均值。求解这个最大化问题，需将w限制为单位长度，即 $\sum_i w_i^2 = 1$。然后使用拉格朗日乘数法来进行求解。但是投影存在一定的重叠现象，如下图。

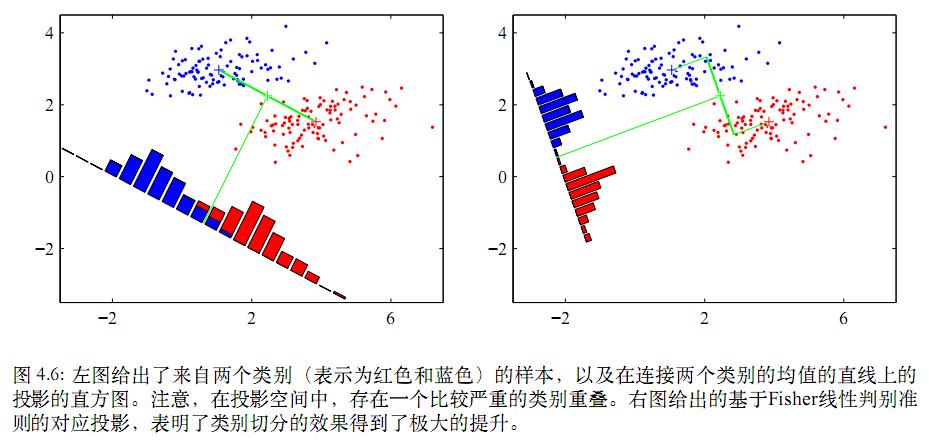
LDA的思想是最大化一个函数使类间均值的投影分得很开，同时让类内方差小，最小化类间重叠。
类内方差： $s_k^2=\sum_{n\in C_k}(y_n-m_k)^2$，其中 $y_n=w^Tx_n$是第n个样本投影后的值。整个数据集的总类内方差定义为 $s_1^2+s_2^2$。
Fisher准则根据类间方差和类内方差的比值定义，即
$$J(w)=\frac{(m_2-m_1)^2}{s_1^2+s_2^2}$$
将 $y=w^Tx$, $m_k=w^Tm_k$, $s_k^2=\sum_{n\in C_k}(y_n-m_k)^2$代入上式子，可以将 $J(w)$重写为：
$$J(w)=\frac{w^TS_Bw}{w^TS_Ww}$$
$(m_2-m_1)^2=(w^Tm_2-w^Tm_1)^2=w^T(m_2-m_1)(m_2-m_1)^T=w^TS_Bw$
$S_B=(m_2-m_1)(m_2-m_1)^T$是类间（between-class）协方差矩阵，是两个向量的外积，虽未矩阵，但秩为1；
$S_W=\sum_{n\in C_1}(x_n-m_1)(x_n-m_1)^T+\sum_{n\in C_2}(x_n-m_2)(x_n-m_2)^T$是类内（within-class）协方差矩阵；
在求导之前，需要对分母进行归一化，令|| $w^TS_Ww$||=1，加入拉格朗日乘子后，关于w求导：
$c(w)=w^TS_Bw-\lambda (w^TS_Ww)\Rightarrow \frac{dc}{dw}=2S_Bw-2\lambda S_Ww=0\Rightarrow S_Bw=\lambda S_Ww$
这里用来矩阵微积分，求导时把 $w^TS_Bw$看成 $S_Bw^2$。
如果 $S_W$可逆，上面结果两边同时乘以 $S_W^{-1}$，得
$$S_W^{-1}S_Bw=\lambda w$$
从上式可知，w就是矩阵 $S_W^{-1}S_B$的特征向量
令 $S_Bw=(m_2-m_1)(m_2-m_1)^Tw=(m_2-m_1)*\lambda _w$
则 $S_W^{-1}S_Bw=S_W^{-1}(m_2-m_1)*\lambda _w=\lambda w$
由于对w缩放大小不影响结果，因此可以约去两边的未知常数 $\lambda _w$和 $\lambda$,得到
$$w = S_W^{-1}(m_2-m_1)$$
这个结果就是Fisher线性判别函数，严格来说只是对于数据向一维投影的方向的一个具体选择而已。投影的数据可以接下来被用于构建判别函数。

多分类情况

假设输入样本数据的维度D大于类别数K。然后引入D’>1个线性”特征”$y_k=w_k^Tx$,其中k=1,…,D’。将这些特征组成向量y。权重向量$w_k$也构成矩阵W的每一列，得到

$$y=W^Tx$$
类内协方差矩阵推广到K类，有
$$S_W=\sum_{k=1}^K S_k$$
其中
$$S_k=\sum_{n\in C_k}(x_n-m_k)(x_n-m_k)^T$$
$$m_k=\frac{1}{N_k}\sum_{n\in C_k}x_n$$
为了找到类间协方差矩阵的推广,先求整体的协方差矩阵
$$S_T=\sum_{n=1}^N(x_n-m)(x_n-m)^T$$
m为全体数据的均值 $m=\frac{1}{N}\sum_{n=1}^Nx_n=\frac{1}{N}\sum_{n=1}^KN_km_k$
整体的协方差矩阵可以分解为之前给的类内协方差矩阵再加上另一个矩阵 $S_B$，它可以看成类间协方差矩阵。
$$S_T=S_W+S_B$$
其中
$$S_B=\sum_{k=1}^KN_k(m_k-m)(m_k-m)^T$$
以上是定义在原始的x空间中。现在在投影到D’维的y空间中定义类似的矩阵：
$$S_W=\sum_{k=1}^K\sum_{n\in C_k}(y_n-u_k)(y_n-u_k)$$
$$S_B=\sum_{k=1}^KN_k(u_k-u)(u_k-u)^T$$
其中
$$u_k=\frac{1}{N_k}\sum_{n\in C_k}y_n,u=\frac{1}{N}\sum_{k=1}^KN_ku_k$$
$S_W = W^Ts_WW,S_B = W^Ts_BW$
W是基向量矩阵，
$$J(w) = \frac{S_B}{S_W} = \frac{W^Ts_BW}{W^Ts_WW}$$
问题又回到求 $J(W)$的最大值上，得到结论 $s_W^{-1}s_Bw_i = \lambda w_i$
最终本质问题还是求矩阵的特征值，首先求出 $s_W^{-1}s_B$的特征值，然后取前K个特征向量组成W矩阵。

$S_B$中的$(m_k-m)$秩为1，因为矩阵的秩小于等于各个相加矩阵的秩之和，所以$S_B$的秩至多为K。知道前K-1个$m_k$之后，最后一个$m_K$可以用前面的$m_k$来线性表示，所以S_B的秩最多为K-1。LDA的使用有限制，至多可生成K-1维子空间，不适合对非高斯分布样本进行降维，样本分类信息依赖方差而不是均值时，效果不好。
$S_W^{-1}S_B$不一定是对称阵，得到的D’个特征向量不一定正交，这与PCA不同。PCA 是无监督的，它所做的只是将整组数据整体映射到最方便表示这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息用主要的特征代替其他相关的非主要的特征，所有特征之间的相关度越高越好。 但是分类任务的特征可能是相互独立的，LDA是有监督的，使得类别内的点距离越近越好（集中），类别间的点越远越好[5]。

原文链接http://blog.csdn.net/u011285477/article/details/51086285

参考资料：
[1]Pattern Recognition and Machine Learning(PRML)
[2]http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html
[3]http://blog.csdn.net/yihaizhiyan/article/details/7579506
[4]http://blog.csdn.net/warmyellow/article/details/5454943
[5]http://blog.csdn.net/jojozhangju/article/details/19652453?utm_source=tuicool&utm_medium=referral