Please implement a simple linear regression model using Python, using gradient descent. The function is defined as def linear_regression_gradient_descent(X, y, learning_rate, iterations), where X is the feature data (two-dimensional array or list), y is the target data (one-dimensional array or list), learning_rate is the learning rate, and iterations is the number of iterations for gradient descent.
The return value of the function is a tuple, containing the coefficients and intercept of the model这个是我的问题,以下之我的解决步骤,section_number: 1
section_description: Identify the task of implementing a linear regression model with gradient descent
section_content:
step1: [思考开始]
Alright, I need to implement a simple linear regression model using Python, specifically using gradient descent. The function is defined as def linear_regression_gradient_descent(X, y, learning_rate, iterations), where X is the feature data, which is a two-dimensional array or list, y is the target data, a one-dimensional array or list, learning_rate is the learning rate for gradient descent, and iterations is the number of iterations for gradient descent. The function should return a tuple containing the coefficients and intercept of the model.
***
***
section_number: 2
section_description: Understanding of linear regression and gradient descent
section_content:
step2: First, I need to understand what linear regression is. It's a statistical method that allows us to summarize and study relationships between continuous variables. In this case, we have multiple features since X is a two-dimensional array, which means it's multiple linear regression.
step3: In multiple linear regression, the model can be represented as:
step4: y = b1*x1 + b2*x2 + ... + bn*xn
step5: Where:
- y is the dependent variable (target)
- x1, x2, ..., xn are the independent variables (features)
- b0 is the intercept
- b1, b2, ..., bn are the coefficients for each feature
step6: I need to find the values of b0, b1, ..., bn that minimize the cost function, which is typically the mean squared error between the predicted values and the actual values.
step7: Gradient descent is an optimization algorithm that can be used to find the values of these coefficients and intercept by iteratively updating them in the direction of the steepest descent of the cost function.
***
***
section_number: 3
section_description: Plan to implement gradient descent for finding coefficients
section_content:
step8: So, my task is to implement gradient descent to find the best values for b0 and b1, b2, etc.
step9: First, I need to initialize the coefficients and intercept. Usually, we initialize them to zero or some random values. For simplicity, I'll initialize them to zero.
step10: Next, I need to define the cost function, which is the mean squared error.
step11: Then, I need to compute the gradients of the cost function with respect to each coefficient and the intercept. These gradients will tell me how to adjust the coefficients and intercept to reduce the cost.
step12: After computing the gradients, I'll update the coefficients and intercept by subtracting the gradients multiplied by the learning rate.
step13: I need to repeat this process for a specified number of iterations.
step14: Finally, I'll return the coefficients and intercept as a tuple.
***
***
section_number: 4
section_description: Handling of data dimensions and intercept separately
section_content:
step15: Let me think about how to handle the data. X is a two-dimensional array or list, so it should have multiple features. y is a one-dimensional array or list.
step16: I need to make sure that X and y have compatible dimensions.
step17: Also, I need to handle the intercept. In multiple linear regression, the intercept can be considered as a coefficient for a feature that is always 1.
step18: To make the implementation easier, I can add a column of ones to X for the intercept.
step19: Wait, but the problem says to return the intercept separately, not as part of the coefficients. So, I need to keep track of the intercept separately.
step20: Alternatively, I can include the intercept in the coefficients by adding a column of ones to X, and then the first coefficient will be the intercept.
step21: But the problem asks for a tuple containing the coefficients and intercept, so perhaps it's better to keep them separate.
***
***
section_number: 5
section_description: Outline of the implementation steps
section_content:
step22: Let me think about how to implement this.
step23: Initialize the coefficients to a list of zeros, with length equal to the number of features.
step24: Initialize the intercept to zero.
step25: For each iteration:
step26: Compute the predicted values: y_pred = intercept + X.dot(coefficients)
step27: Compute the gradients for the intercept and coefficients.
step28: The gradient for the intercept is the mean of (y_pred - y)
step29: The gradient for each coefficient is the mean of (y_pred - y) * X[:, feature_index]
step30: Update the intercept and coefficients:
step31: intercept = intercept - learning_rate * gradient_intercept
step32: coefficients = coefficients - learning_rate * gradient_coefficients
step33: After all iterations, return the coefficients and intercept as a tuple.
***
***
section_number: 6
section_description: Considerations for gradient calculations and use of numpy
section_content:
step34: Wait, I need to make sure about the gradient calculations.
step35: In linear regression, the cost function is:
step36: J = (1/(2*m)) * sum((y_pred - y)^2)
step37: Where m is the number of training examples.
step38: The gradients are the partial derivatives of J with respect to each parameter.
step39: For the intercept (b0):
step40: dJ/db0 = (1/m) * sum(y - y_pred)
step41: For each coefficient (b1, b2, ...):
step42: dJ/dbj = (1/m) * sum((y_pred - y) * xj)
step43: Where xj is the j-th feature.
step44: So, I need to compute these gradients and update the parameters accordingly.
step45: I need to make sure that the dimensions match when performing these operations.
step46: Since X is a two-dimensional array, and y is one-dimensional, I need to ensure that the dot product and multiplications are done correctly.
step47: In Python, I can use numpy for numerical operations, but the problem doesn't specify if I can use numpy or if I should implement it using pure Python lists.
step48: Looking back at the problem statement, it says "two-dimensional array or list" and "one-dimensional array or list", so I think I should implement it using pure Python lists without relying on numpy.
step49: But implementing matrix operations with pure Python lists can be cumbersome and inefficient, especially for large datasets.
step50: However, since the problem doesn't specify, I'll assume that I can use numpy for numerical operations, as it's common practice in data science.
***
***
section_number: 7
section_description: Code outline and considerations for potential edge cases
section_content:
step51: So, I'll import numpy at the beginning.
step52: Now, I'll outline the steps in code:
step53: 1. Import numpy.
step54: 2. Define the function linear_regression_gradient_descent(X, y, learning_rate, iterations):
step55: a. Convert X and y to numpy arrays for easier numerical operations.
step56: b. Initialize coefficients to a list of zeros with length equal to the number of features.
step57: c. Initialize intercept to zero.
step58: d. Perform gradient descent for the given number of iterations:
step59: i. Compute y_pred = intercept + X.dot(coefficients)
step60: ii. Compute the error: y_pred - y
step61: iii. Compute the gradient for the intercept: (1/m) * np.sum(error)
step62: iv. Compute the gradient for coefficients: (1/m) * np.dot(X.T, error)
step63: v. Update intercept and coefficients:
step64: intercept -= learning_rate * gradient_intercept
step65: coefficients -= learning_rate * gradient_coefficients
step66: e. After all iterations, return the coefficients and intercept as a tuple.
step67: Wait, in step d.iv, np.dot(X.T, error) will give the sum of the product of each feature with the error, which is what we need for the gradients of the coefficients.
step68: But I need to make sure that the dimensions are correct.
step69: Assuming X is of shape (m, n), where m is the number of samples and n is the number of features.
step70: y is of shape (m,).
step71: coefficients is of shape (n,).
step72: intercept is a scalar.
step73: Then, y_pred = intercept + X.dot(coefficients) should be of shape (m,).
step74: error = y_pred - y, shape (m,).
step75: gradient_intercept = (1/m) * np.sum(error)
step76: gradient_coefficients = (1/m) * np.dot(X.T, error), shape (n,)
step77: Then, updating coefficients and intercept:
step78: intercept = intercept - learning_rate * gradient_intercept
step79: coefficients = coefficients - learning_rate * gradient_coefficients
step80: This seems correct.
step81: Now, I need to consider if there is any need to normalize the features or handle scaling, but since the problem doesn't mention it, I'll assume that the features are already scaled appropriately.
step82: Also, I need to make sure that the function returns the coefficients and intercept in a tuple, with coefficients being a list or array, and intercept being a scalar.
step83: I should also think about edge cases, such as:
step84: - If X has only one feature.
step85: - If X has multiple features.
step86: - If the number of samples in X and y don't match.
step87: - If learning_rate is zero or negative.
step88: - If iterations is zero or negative.
step89: I need to handle these cases appropriately, perhaps by adding assertions or checks at the beginning of the function.
step90: But since the problem doesn't specify handling of invalid inputs, I'll assume that the inputs are valid.
step91: Also, I need to make sure that the function is efficient and doesn't have unnecessary computations.
step92: Now, I'll proceed to write the code accordingly.
[思考结束]
***
***
section_number: 8
section_description: Explanation of approach for solving the problem with initialization and gradient descent steps
section_content:
step93: To solve this problem, we need to implement a simple linear regression model using gradient descent in Python. The task is to find the coefficients and intercept of the regression line that minimizes the mean squared error between the predicted and actual target values.
step94: ### Approach
step95: 1. **Initialization**:
- Convert the input feature data `X` and target data `y` into numpy arrays for efficient numerical operations.
- Initialize the coefficients to a list of zeros, with a length equal to the number of features.
- Initialize the intercept to zero.
step96: 2. **Gradient Descent**:
- For a specified number of iterations, perform the following steps:
- Compute the predicted target values using the current coefficients and intercept.
- Calculate the error between the predicted and actual target values.
- Compute the gradients for the intercept and coefficients.
- Update the intercept and coefficients using the gradients and the learning rate.
step97: 3. **Return the Results**:
- After completing the iterations, return the coefficients and intercept as a tuple.
***
***
section_number: 9
section_description: Implementation of the solution using numpy for gradient descent
section_content:
step98: ### Solution Code
step99: ```python
import numpy as np
step100: def linear_regression_gradient_descent(X, y, learning_rate, iterations):
# Convert X and y to numpy arrays
X = np.array(X)
y = np.array(y)
# Number of samples and features
m, n = X.shape
# Initialize coefficients and intercept
coefficients = np.zeros(n)
intercept = 0.0
# Gradient descent
for _ in range(iterations):
# Predicted values
y_pred = intercept + np.dot(X, coefficients)
# Errors
error = y_pred - y
# Gradients
gradient_intercept = (1/m) * np.sum(error)
gradient_coefficients = (1/m) * np.dot(error, X)
# Update intercept and coefficients
intercept -= learning_rate * gradient_intercept
coefficients -= learning_rate * gradient_coefficients
return (coefficients.tolist(), intercept)
```
***
***
section_number: 10
section_description: Detailed explanation of the implementation and results
section_content:
step101: ### Explanation
step102: - **Initialization**:
- We convert `X` and `y` to numpy arrays to leverage numpy's efficient array operations.
- The coefficients are initialized to zeros, and the intercept is initialized to zero.
step103: - **Gradient Descent**:
- For each iteration, we calculate the predicted values (`y_pred`) using the current coefficients and intercept.
- The error is the difference between the predicted and actual target values.
- The gradients for the intercept and coefficients are computed as the mean of the error and the dot product of the feature matrix transpose and the error, respectively.
- The intercept and coefficients are updated by subtracting the learning rate multiplied by their respective gradients.
step104: - **Return the Results**:
- After completing the specified number of iterations, the function returns the coefficients and intercept as a tuple, converting the coefficients back to a list for compatibility.
step105: This approach efficiently finds the optimal coefficients and intercept for the linear regression model using gradient descent.请你根据以下的规则进行标注section_number:准确填写当前标注的 section 的序号。
contain_new_solution:判断当前段落是否开启新的思路尝试,若有则标注 “1”,否则标注 “0” 。若为 “1”,请进一步明确新的思路尝试开始的步骤(填入 new_solution_step )。
idea_correct:判断当前段落内思路是否正确或有用。如果该段落内所采用的思路或方法能在解题中具有实际意义,则标记为 “1”;否则,标记为 “0”。
contain_error:判断当前段落是否存在错误。若存在错误,该字段标记为 “1”,并需继续填写后续错误相关字段;若不存在错误,则标记为 “0”,可跳过错误相关字段,直接进行下一项标注。
error_step:若当前段落存在错误,则需详细记录具体是在哪一步出错。
explanation:用一句话简单描述错误原因。
correction:给出该步骤的正确推理或计算过程。
contain_reflection:判断该段落是否包含正向的反思。如果段落中有对错误或思路的积极反思,则标记为 “1”,否则标记为 “0”。若标记为 “1”,需记录反思从哪个步骤开始(填入 reflection_start_step )请你将上述的10个section,进行标注


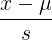 ,其中
,其中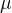 为均值,s为特征的范围,即max-min。也可以用标准差。
为均值,s为特征的范围,即max-min。也可以用标准差。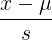 ,其中
,其中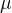 为均值,s为特征的范围,即max-min。也可以用标准差。
为均值,s为特征的范围,即max-min。也可以用标准差。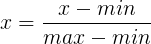
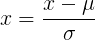
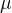 为均值,
为均值,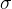 标准差。标准差是方差的开方,把标注差公式也贴上来吧:
标准差。标准差是方差的开方,把标注差公式也贴上来吧: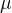 为均值,
为均值,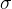 标准差。标准差是方差的开方,把标注差公式也贴上来吧:
标准差。标准差是方差的开方,把标注差公式也贴上来吧: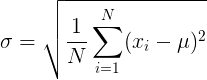





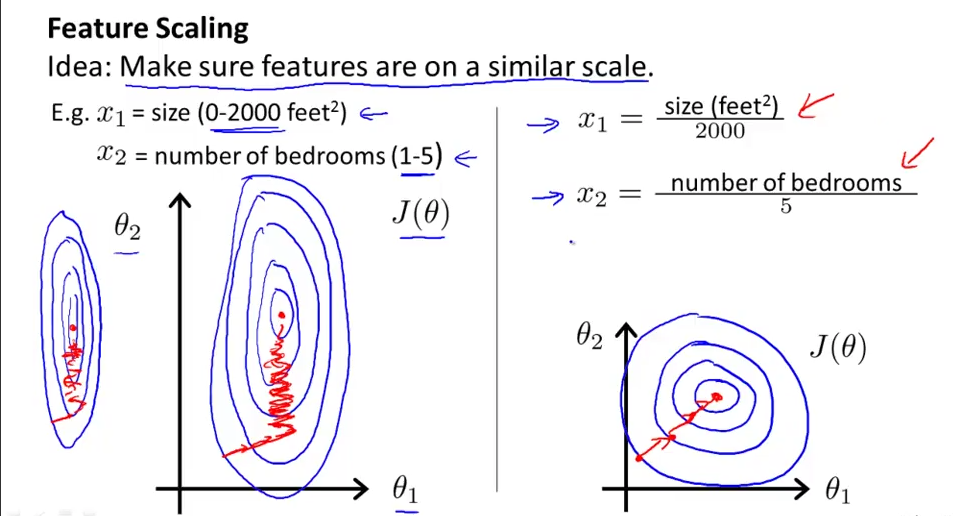
 本文介绍特征缩放对梯度下降算法的重要性及其实现方法,包括特征缩放的目的、常用范围以及两种归一化方法:min-max标准化和0均值标准化,并探讨了它们的适用场景。
本文介绍特征缩放对梯度下降算法的重要性及其实现方法,包括特征缩放的目的、常用范围以及两种归一化方法:min-max标准化和0均值标准化,并探讨了它们的适用场景。
















 858
858

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








