十五、多项式乘法与快速傅里叶变换
前言
经典算法研究系列,已经写到第十五章了,本章,咱们来介绍多项式的乘法以及快速傅里叶变换算法。本博客之前也已详细介绍过离散傅里叶变换(请参考:十、从头到尾彻底理解傅里叶变换算法、上,及十、从头到尾彻底理解傅里叶变换算法、下),这次咱们从多项式乘法开始,然后介绍FFT算法的原理与实现。同时,本文虽涉及到不少数学公式和定理(当然,我会尽量舍去一些与本文咱们要介绍的中心内容无关的定理或证明,只为保证能让读者易于接受或理解),但尽量保证通俗易懂,以让读者能看个明白。
有朋友建议,算法专一种,就ok,没必要各个都学习。但个人实在抑制不住自己的兴趣,就是想写,当没法做到强迫自己不写时,这个经典算法研究系列便一直这么写下来了。
第一节、多项式乘法
我们知道,有两种表示多项式的方法,即系数表示法和点值表示法。什么是系数表示法?所谓的系数表示法,举个例子如下图所示,A(x)=6x^3 + 7x^2 - 10x + 9,B(x)=-2x^3+4x-5,则C(x)=A(x)*B(x)就是普通的多项式相乘的算法,系数与系数相乘,这就是所谓的系数表示法。
那么,何谓点值表示法?。一个次数为n次的多项式A(x)的点值表示就是n个点值所形成的集合:{(x0,y0), (x1,y1),..., (xn-1,yn-1)}。其中所有xk各不相同,且当k=0,1,……,n-1时,有y(k)=A(xk)。
一个多项式可以由很多不同的点值表示,这是由于任意n个相异点x0,x1,...,xn-1组成的集合,都可以看做是这种点值法的表示方法。对于一个用系数形式表示的多项式来说,在原则上计算其点值表示是简单易行的,我们只需要选取n个相异点x0,x1,...,xn-1,然后对k=0,1,...,n-1,求出A(xk),然后根据霍纳法则,求出这n个点的值所需要的时间为O(n^2)。
然,稍后,你将看到,如果巧妙的选取xk的话,适当的利用点值表示可以使多项式的乘法可以在线性时间内完成。所以,如果我们能恰到好处的利用系数表示法与点值表示法的相互转化,那么我们可以加速多项式乘法(下面,将详细阐述这个过程),达到O(n*logn)的最佳时间复杂度。
前面说了,当用系数表示法,即用一般的算法表示多项式时,两个 n次多项式的乘法需要用 O(n^2)的时间才能完成。但采用点值表示法时,多项式乘法的运行时间仅为O(n)。接下来,咱们要做的是,如何利用系数表示法与点值表示法的相互转化来实现多项式系数表示法的O(n*logn)的快速乘法。
第二节、多项式的快速乘法
在此之前,我们得明白两个概念,求值与插值。通俗的讲,所谓求值(系数->点值),是指系数形式的多项式转换为点值形式的表示方式。而插值(点值->系数)正好是求值的逆过程,即反过来,它是已知点值表示法,而要你转换其为多项式的系数表示法(用n个点值对也可以唯一确定一个不超过n-1次多项式,这个过程称之为插值)。而这个系数表示法与点值表示法的相互转化,即无论是从系数表示法转化到点值表示法所谓的求值,还是从点值表示法转化到系数表示法所谓的插值,求值和插值两种过程的时间复杂度都是O(n*logn)。
前面,我们已经说了,在多项式乘法中,如果用系数表示法表示多项式,那么多项式乘法的复杂度将为O(n^2),而用点值表示法表示的多项式,那么多项式的乘法的复杂度将是线性复杂度为O(n),即: 适当的利用点值表示可以使多项式的乘法可以在线性时间内完成。此时读者可以发挥你的想象,假设我们以下面这样一种过程来计算多项式的乘法(不过在此之前,你得先把两个要相乘的多项式A(x)和B(x)扩充为次数或者说系数为2n次的多项式),我们将会得到我们想要的结果:
- 系数表示法转化为点值表示法。先用系数表示法表示一个多项式,然后对这个多项式进行求值操作,即多项式从系数表示法变成了点值表示法,时间复杂度为O(n*logn);
- 点值表示法计算多项式乘法。用点值表示法表示多项式后,计算多项式的乘法,线性复杂度为O(n);
- 点值表示法转化为系数表示法。最终再次将点值表示法表示的多项式转变为系数表示法表示的多项式,这一过程,为O(n*logn)。
那么,综上上述三项操作,系数表示法表示的多项式乘法总的时间复杂度已被我们降到了O(n*logn+n+n*logn)=O(N*logN)。
如下图所示,从左至右,看过去,这个过程即是完成多项式乘法的计算过程。不过,完成这个过程有两种方法,一种就是前面第一节中所说的普通方法,即直接对系数表示法表示的多项式进行乘法运算,复杂度为O(n^2),它体现在下图中得Ordinary multiplication过程。还有一种就是本节上文处所述的三个步骤:1、将多项式由系数表示法转化为点值表示法(点值过程);2、 利用点值表示法完成多项式乘法;3、将点值表示法再转化为系数表示法(插值过程)。三个步骤下来,总的时间复杂度为O(N*logN)。它体现在下图中的Evaluation + Pointwise multiplication + Interpolation 三个合过程。
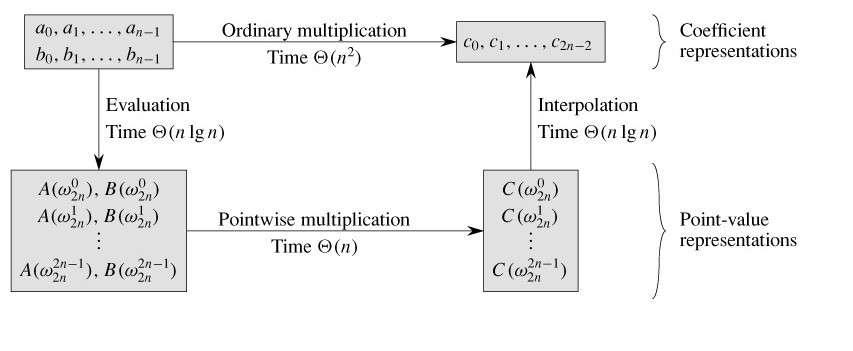
由上图中,你也已经看到了。我们巧妙的利用了关于点值形式的多项式的线性时间乘法算法,来加快了系数形式表示的多项式乘法的运算速度。在此过程中,我们的工作最关键的就在于以O(n*logn)的时间快速把一个多项式从系数形式转换为点值形式(求值,我们即称之为FFT),然后再以O(n*logn)的时间从点值形式转换为系数形式(插值,我们即称之为FFT逆)。最终达到了我们以最终的系数形式表示的多项式的快速乘法为O(N*logN)的时间复杂度。好不令人心生快意。
对上图,有一点必须说明,项w2n是2n次单位复根。且不容忽视的是,在上述两种表示法即系数表示法和点值表示法相互转换的过程中, 都使用了单位复根,才得以在O(n*logn)的时间内完成求值与插值运算(至于何谓单位复根,请参考相关资料。因为为了保证本文的通俗易懂性,无意引出一大堆公式或定理)。
第三节、FFT
注:本节有相当部分文字来自算法导论中文版第二版以及维基百科。
在具体介绍FFT之前,我们得熟悉知道折半定理是怎么一回事儿:如果n>0且n为偶数,那么,n个n次单位复根的平方等于n/2个n/2个单位复根。我们已经知道,通过使用一种称为快速傅里叶变换(FFT)的方法,可以在O(n*logn)的时间内计算出DFTn(a),而若采用直接的方法复杂度为O(n^2)。FFT就是利用了单位复根的特殊性质。
你将看到,FFT方法运用的策略为分治策略,所谓分治,即分而治之。两个多项式A(x)与B(x)相乘的过程中,FFT用A(x)中偶数下标的系数与奇数下标的系数,分别定义了两个新的次数界为n/2的多项式A[0](x)和A[1](x):
A[0](x) =a0 +a2x +a4x2 +··· +an-2xn/2-1,
A[1](x) =a1 +a3x +a5x2 +··· +an-1xn/2-1.
注意,A[0]包含了A中所有偶数下标的系数(下标的相应二进制数的最后一位为0),而A[1]包含A中所有奇数下标的系数(下标的相应二进制数的最后一位为1)。有下式:
这样,求A(x)在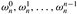 处的问题就转换为:
处的问题就转换为:
1)求次数界为n/2的多项式A[0]与A[1]在点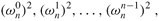 的值,然后
的值,然后
2)将上述结果进行组合。
下面,我们用N次单位根WN来表示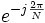 。
。
WN的性质:
- 周期性,WN具有周期N。
- 对称性:
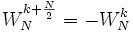 。
。 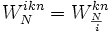
为了简单起见,我们下面设待变换序列长度n = 2r。 根据上面单位根的对称性,求级数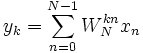 时,可以将求和区间分为两部分:
时,可以将求和区间分为两部分:
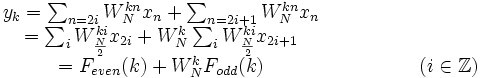
Fodd(k) 和 Feven(k)是两个分别关于序列 奇数号和偶数号序列N/2点变换。由此式只能计算出yk的前N/2个点,对于后N/2个点,注意Fodd(k) 和 Feven(k) 都是周期为N/2的函数,由单位根的对称性,于是有以下变换公式:
奇数号和偶数号序列N/2点变换。由此式只能计算出yk的前N/2个点,对于后N/2个点,注意Fodd(k) 和 Feven(k) 都是周期为N/2的函数,由单位根的对称性,于是有以下变换公式:
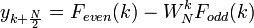
 。
。
这样,一个N点变换就分解成了两个N/2点变换,照这样可继续分解下去。这就是库利-图基快速傅里叶变换算法的基本原理。此时,我们已经不难分析出此时算法的时间复杂度将为O(NlogN)。
ok,没想到,本文之中还是出现了这么多的公式(没办法,搞这个FFT就是个纯数学活儿。之前买的一本小波与傅里叶分析基础也是如此,就是一本数学公式和定理的聚集书。不过,能看懂更好,实在无法弄懂也只权当做个稍稍了解)。
好了,下面,咱们来简单理解下FFT中的蝶形算法,本文将告结束。如下图所示:
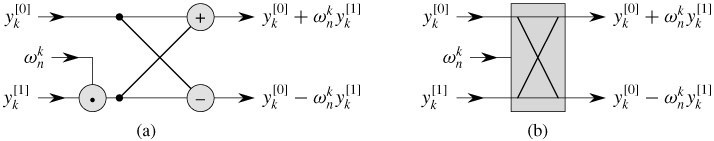
有人这样解释蝶形算法:对于N(2的x次方)点的离散信号,把它按索引位置分成两个序列,分别为0,2,4,....,2K(记为A)和1,3,5,....,2K-1(记为B),由傅立叶变换可以推出N点的傅立叶变换前半部分的结果为A+B*旋转因子,后半部分的结果为A-B*旋转因子。于是求N点的傅立叶变换就变成分别求两个N/2点序列的傅立叶变换,对每一个N/2点的序列,递归前面的步骤,直到只有两点的序列,就只变成简单的加减关系了。把这些点的加减关系用线连接,看上去就是个蝶形。ok,更多可参考算法导论第30章。
举一个例子,我们知道,4X4的矩阵运算如果按常规算法的话仍要进行64次乘法运算和48次加法,这将耗费较多的时间,于是在H.264中,有一种改进的算法(蝶形算法)可以减少运算的次数。这种矩阵运算算法构造非常巧妙,利用构造的矩阵的整数性质和对称性,可完全将乘法运算转化为加法运算。如下图所示:
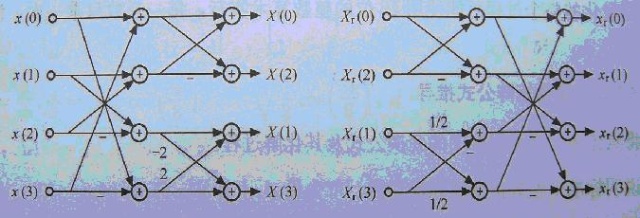
下面的代码来自一本数字图像处理的书上的源代码:
VOID WINAPI FFT(complex<double> * TD, complex<double> * FD, int r)
{
// 付立叶变换点数
LONG count;
// 循环变量
int i,j,k;
// 中间变量
int bfsize,p;
// 角度
double angle;
complex<double> *W,*X1,*X2,*X;
// 计算付立叶变换点数
count = 1 << r;
// 分配运算所需存储器
W = new complex<double>[count / 2];
X1 = new complex<double>[count];
X2 = new complex<double>[count];
// 计算加权系数
for(i = 0; i < count / 2; i++)
{
angle = -i * PI * 2 / count;
W[i] = complex<double> (cos(angle), sin(angle));
}
// 将时域点写入X1
memcpy(X1, TD, sizeof(complex<double>) * count);
// 采用蝶形算法进行快速付立叶变换
for(k = 0; k < r; k++)
{
for(j = 0; j < 1 << k; j++)
{
bfsize = 1 << (r-k);
for(i = 0; i < bfsize / 2; i++)
{
p = j * bfsize;
X2[i + p] = X1[i + p] + X1[i + p + bfsize / 2];
X2[i + p + bfsize / 2] = (X1[i + p] - X1[i + p + bfsize / 2]) * W[i * (1<<k)];
}
}
X = X1;
X1 = X2;
X2 = X;
}
// 重新排序
for(j = 0; j < count; j++)
{
p = 0;
for(i = 0; i < r; i++)
{
if (j&(1<<i))
{
p+=1<<(r-i-1);
}
}
FD[j]=X1[p];
}
// 释放内存
delete W;
delete X1;
delete X2;
}待我日后继续斟酌,补充。完。
updated:关于快速傅立叶变换(FFT)的C++实现与Matlab实验,这里有一篇不错的文章,读者可以看看:http://blog.csdn.net/rappy/article/details/1700829。2012.03.03。






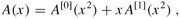

















 1977
1977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










