梯度下降法(gradient descent),又名最速下降法(steepest descent)是求解无约束最优化问题最常用的方法,它是一种迭代方法,每一步主要的操作是求解目标函数的梯度向量,将当前位置的负梯度方向作为搜索方向(因为在该方向上目标函数下降最快,这也是最速下降法名称的由来)。
梯度下降法特点:越接近目标值,步长越小,下降速度越慢。
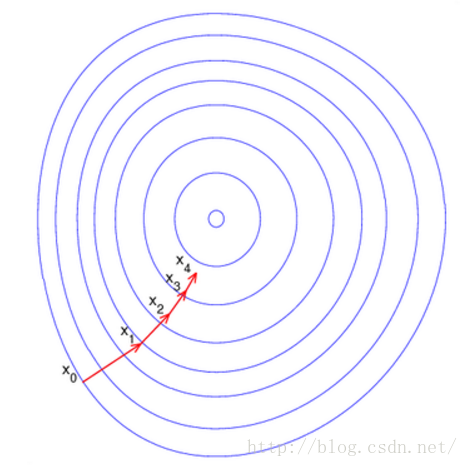
直观上来看如下图所示:
这里每一个圈代表一个函数梯度,最中心表示函数极值点,每次迭代根据当前位置求得的梯度(用于确定搜索方向以及与步长共同决定前进速度)和步长找到一个新的位置,这样不断迭代最终到达目标函数局部最优点(如果目标函数是凸函数,则到达全局最优点)。
下面我们将通过公式来具体说明梯度下降法
下面这个h(θ)是我们的拟合函数
也可以用向量的形式进行表示:
下面函数是我们需要进行最优化的风险函数,其中的每一项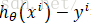
这里我们乘上1/2是为了方便后面求偏导数时结果更加简洁,之所以能乘上1/2是因为乘上这个系数后对求解风险函数最优值没有影响。
我们的目标就是要最小化风险函数,使得我们的拟合函数能够最大程度的对目标函数y进行拟合,即:
后面的具体梯度求解都是围绕这个目标来进行。
批量梯度下降BGD
按照传统的思想,我们需要对上述风险函数中的每个
这里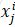
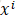
接下来由于我们要最小化风险函数,故按照每个参数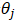
这里的α表示每一步的步长
从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果m很大,那么可想而知这种方法的迭代速度!!所以,这就引入了另外一种方法,随机梯度下降。
随机梯度下降SGD
因为批量梯度下降在训练集很大的情况下迭代速度非常之慢,所以在这种情况下再使用批量梯度下降来求解风险函数的最优化问题是不具有可行性的,在此情况下,提出了——随机梯度下降
我们将上述的风险函数改写成以下形式:
其中,
称为样本点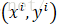
接下来我们对每个样本的损失函数,对每个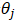
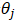
然后根据每个参数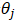
与批量梯度下降相比,随机梯度下降每次迭代只用到了一个样本,在样本量很大的情况下,常见的情况是只用到了其中一部分样本数据即可将θ迭代到最优解。因此随机梯度下降比批量梯度下降在计算量上会大大减少。
SGD有一个缺点是,其噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。而且SGD因为每次都是使用一个样本进行迭代,因此最终求得的最优解往往不是全局最优解,而只是局部最优解。但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。
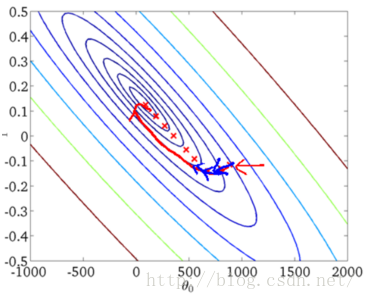
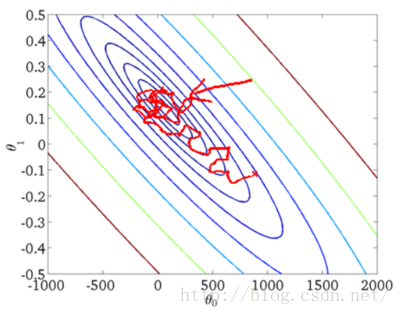
下面是两种方法的图形展示:
从上述图形可以看出,SGD因为每次都是用一个样本点进行梯度搜索,因此其最优化路径看上去比较盲目(这也是随机梯度下降名字的由来)。
对比其优劣点如下:
批量梯度下降:
优点:全局最优解;易于并行实现;总体迭代次数不多
缺点:当样本数目很多时,训练过程会很慢,每次迭代需要耗费大量的时间。
随机梯度下降:
优点:训练速度快,每次迭代计算量不大
缺点:准确度下降,并不是全局最优;不易于并行实现;总体迭代次数比较多。
============ 分割分割 =============
上面我们讲解了什么是梯度下降法,以及如何求解梯度下降,下面我们将通过Python来实现梯度下降法。
# _*_ coding: utf-8 _*_
# 作者: yhao
# 博客: http://blog.csdn.net/yhao2014
# 邮箱: yanhao07@sina.com
# 训练集
# 每个样本点有3个分量 (x0,x1,x2)
x = [(1, 0., 3), (1, 1., 3), (1, 2., 3), (1, 3., 2), (1, 4., 4)]
# y[i] 样本点对应的输出
y = [95.364, 97.217205, 75.195834, 60.105519, 49.342380]
# 迭代阀值,当两次迭代损失函数之差小于该阀值时停止迭代
epsilon = 0.0001
# 学习率
alpha = 0.01
diff = [0, 0]
max_itor = 1000
error1 = 0
error0 = 0
cnt = 0
m = len(x)
# 初始化参数
theta0 = 0
theta1 = 0
theta2 = 0
while True:
cnt += 1
# 参数迭代计算
for i in range(m):
# 拟合函数为 y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]
# 计算残差
diff[0] = (theta0 + theta1 * x[i][1] + theta2 * x[i][2]) - y[i]
# 梯度 = diff[0] * x[i][j]
theta0 -= alpha * diff[0] * x[i][0]
theta1 -= alpha * diff[0] * x[i][1]
theta2 -= alpha * diff[0] * x[i][2]
# 计算损失函数
error1 = 0
for lp in range(len(x)):
error1 += (y[lp]-(theta0 + theta1 * x[lp][1] + theta2 * x[lp][2]))**2/2
if abs(error1-error0) < epsilon:
break
else:
error0 = error1
print ' theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f' % (theta0, theta1, theta2, error1)
print 'Done: theta0 : %f, theta1 : %f, theta2 : %f' % (theta0, theta1, theta2)
print '迭代次数: %d' % cnt
结果(截取部分):
theta0 : 2.782632, theta1 : 3.207850, theta2 : 7.998823, error1 : 7.508687
theta0 : 4.254302, theta1 : 3.809652, theta2 : 11.972218, error1 : 813.550287
theta0 : 5.154766, theta1 : 3.351648, theta2 : 14.188535, error1 : 1686.507256
theta0 : 5.800348, theta1 : 2.489862, theta2 : 15.617995, error1 : 2086.492788
theta0 : 6.326710, theta1 : 1.500854, theta2 : 16.676947, error1 : 2204.562407
theta0 : 6.792409, theta1 : 0.499552, theta2 : 17.545335, error1 : 2194.779569
theta0 : 74.892395, theta1 : -13.494257, theta2 : 8.587471, error1 : 87.700881
theta0 : 74.942294, theta1 : -13.493667, theta2 : 8.571632, error1 : 87.372640
theta0 : 74.992087, theta1 : -13.493079, theta2 : 8.555828, error1 : 87.045719
theta0 : 75.041771, theta1 : -13.492491, theta2 : 8.540057, error1 : 86.720115
theta0 : 75.091349, theta1 : -13.491905, theta2 : 8.524321, error1 : 86.395820
theta0 : 75.140820, theta1 : -13.491320, theta2 : 8.508618, error1 : 86.072830
theta0 : 75.190184, theta1 : -13.490736, theta2 : 8.492950, error1 : 85.751139
theta0 : 75.239442, theta1 : -13.490154, theta2 : 8.477315, error1 : 85.430741
theta0 : 97.986390, theta1 : -13.221172, theta2 : 1.257259, error1 : 1.553781
theta0 : 97.986505, theta1 : -13.221170, theta2 : 1.257223, error1 : 1.553680
theta0 : 97.986620, theta1 : -13.221169, theta2 : 1.257186, error1 : 1.553579
theta0 : 97.986735, theta1 : -13.221167, theta2 : 1.257150, error1 : 1.553479
theta0 : 97.986849, theta1 : -13.221166, theta2 : 1.257113, error1 : 1.553379
theta0 : 97.986963, theta1 : -13.221165, theta2 : 1.257077, error1 : 1.553278
Done: theta0 : 97.987078, theta1 : -13.221163, theta2 : 1.257041
迭代次数: 3443可以看到最后收敛到稳定的参数值。
注意:这里在选取alpha和epsilon时需要谨慎选择,可能不适的值会导致最后无法收敛。
参考文档:
随机梯度下降(Stochastic gradient descent)和 批量梯度下降(Batch gradient descent )的公式对比、实现对比
随机梯度下降法
python实现梯度下降算法








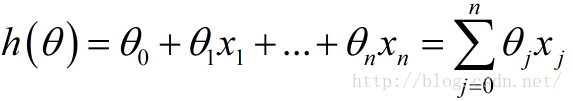
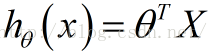
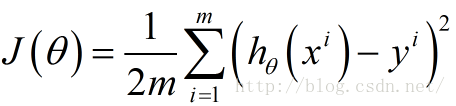
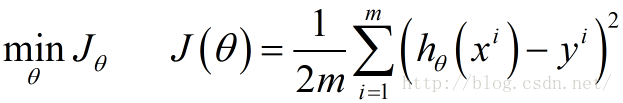
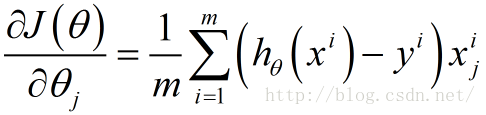
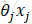
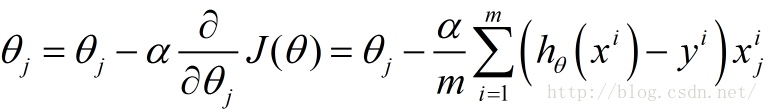
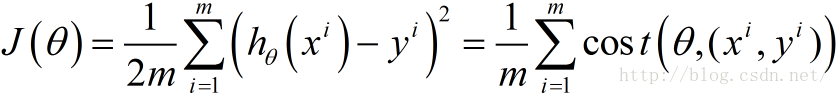
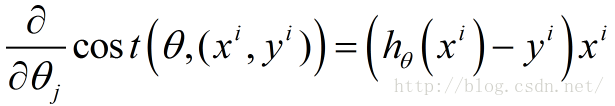
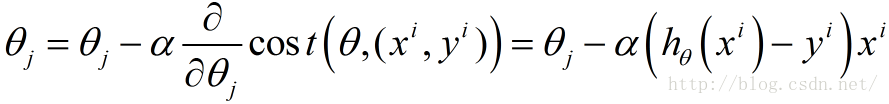
















 369
369

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








