ML—SVM导论

Andrew Zhang
Tianjin Key Laboratory of Cognitive Computing and Application
Tianjin University
Oct 23, 2015

本篇博客用来总结对SVM理论的理解，以及学习过程中思考的一些问题。

一、SVM模型建立
对于线性可分的数据，SVM指导思想是寻找一个分类超平面，将两类样本分别划分到超平面两侧，并且使得每类的样本与分类超平面的距离达到最大。其中，每个类别中与分类超平面最近的点被称为支持向量。并且，容易知道，每个类别的支持向量到分类超平面的距离相等的时候才能达到最优分类超平面。
数学公式对SVM模型的描述如下。
假设n维空间的分类超平面是$w^Tx+b=0$。则任意一点(x,y)到这个超平面的距离为$\frac{|w^Tx+b|}{||w||_2}$。而SVM的目标就是寻找可以正确区分所有样本的w,b，并使得对于任意一个支持向量(x,y)有
$max\frac{|w^Tx+b|}{||w||_2}\tag{1-1}$
由于同一个分类超平面w，b可以成比例的放缩。因此总可以经过适当的放缩找到合适的w,b使得支持向量处的$w^Tx+b$值为1或-1。所以这时目标公式(1)就简化为
$max\frac{1}{||w||_2}\tag{1-2}$
而此时的约束条件可以表达为
$y_i(w^Tx_i+b)\geq1, i=1,2,...,m\tag{1-3}$

在实际应用过程中一般采用的(1-2)的另一种等价凸函数形式，见公式(1-4)，因此问题转化为(1-4,5)。
$min\frac{1}{2}||w||^2\tag{1-4}$
$y_i(w^Tx_i+b)\geq1, i=1,2,...,m\tag{1-5}$

二、SVM模型求解
如果新手，建议先看参考博客[1]。
首先把SVM模型对应的公式(1-4,5)转化为如下的标准形式
$minf(w,b)=\frac{1}{2}||w||^2\tag{2-1}$
$g_i(w,b)=1-y_i(w^Tx_i+b)\leq0, i=1,2,...,m\tag{2-2}$
很显然$f(w,b),g_i(w,b)$ 都是凸函数。为了利用对偶求解，需要对模型表达式(2-1,2)进行一次等价变换，变换后的表达式如下：
$min_{w,b}max_{\alpha_i\geq0}\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i{g_i(w,b)}\tag{2-3}$
其中，一般把$L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i{g_i(w,b)}$称作拉格朗日函数。
根据参考博客[1] 容易知道公式(2-3)的对偶问题为
$max_{\alpha_i\geq0}min_{w,b}L(w,b,\alpha)=max_{\alpha_i\geq0}min_{w,b}\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i{g_i(w,b)}\tag{2-4}$
并且根据Slater条件容易知道原问题和对偶问题属于强对偶问题，即在原问题和对偶问题都取最优解的时候，两个的最优解是相等的，并且最优解对应的$\alpha,w,b$是相等的。因此可以根据对偶问题对原问题进行求解。
对于对偶问题可以划分成两步进行求解。首先对于内层问题
$\theta_D(\alpha)=min_{w,b}L(w,b,\alpha)=min_{w,b}\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i{g_i(w,b)}\tag{2-5}$
内层问题(2-5)属于无约束优化问题，又由于其中的函数是凸函数，所以他们的极小值肯定存在且在驻点处取得。因此可得如下两个等式。
$\frac{∂}{∂w}L(w,b,\alpha)=w-\sum_{i=1}^{m}\alpha_i{y_ix_i}=0\tag{2-6}$
$\frac{∂}{∂b}L(w,b,\alpha)=\sum_{i=1}^{m}\alpha_i{y_i}=0\tag{2-7}$
由公式(2-6)可得
$w=\sum_{i=1}^{m}\alpha_i{y_ix_i}\tag{2-8}$
将公式(2-7,8)带入公式(2-5)可将公式(2-5)转化为
$\theta_D(\alpha)=\sum_{i=1}^{m}{\alpha_i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j<x_i,x_j>\tag{2-9}$
对偶问题转化为
$max \theta_D(\alpha)=\sum_{i=1}^{m}{\alpha_i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j<x_i,x_j>\tag{2-10}$
这时的约束条件应该为

$$\begin{Bmatrix} \alpha_i\geq0,i=1,2,...,m\\ \sum_{i=1}^{m}\alpha_iy_i=0 \end{Bmatrix}\tag{2-11}$$
其中，SVM判别函数为
$w^Tx+b=(\sum_{i=1}^{m}{\alpha_iy_ix_i})^Tx+b=\sum_{i=1}^{m}\alpha_iy_i<x_i,x>+b\tag{2-12}$
并且，很容易得到
$b=-\frac{1}{2}(max_{y_i=-1}w^Tx_i+min_{y_i=1}w^Tx_i)\tag{2-13}$
对以上一些公式的简单分析：
分析1. 通过公式(2-12,13)可以发现对测试样本做预测的时候我们只需要知道 $\alpha_i$ 即可。
分析2. 根据参考博客kkt-3， $\alpha_i>0$的时候必有 $g_i(w,b)=0$，若 $g_i(w,b)<0$,必有 $\alpha_i=0$ 。注：对于支持向量处有 $g_i(w,b)=0$，非支持向量处大于号成立.
分析3. SVM模型的求解转化为公式(2-10,11)，SVM预测转化为公式(12,13)。容易发现模型整个算法(模型训练和模型预测)是与输入样本之间特征的内积有关。这个性质是SVM的核技巧的基础。

三、核技巧
核技巧是寄希望于通过将原始的n维向量内积扩展到更高维的空间上的内积，使得在n维空间中线性不可分的数据在高维空间变得线性可分。
例如，图一所示为二维空间的线性不可分样本

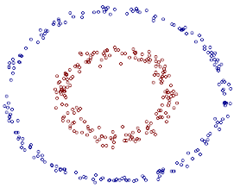
但是如果在三维空间是如图二所示的话

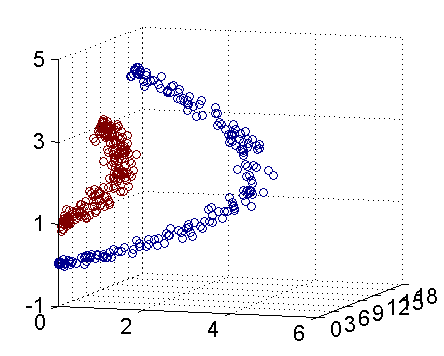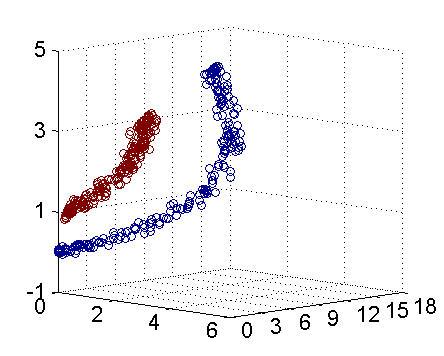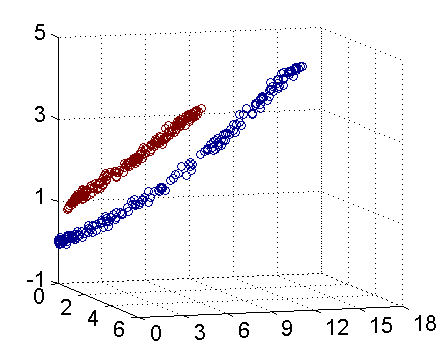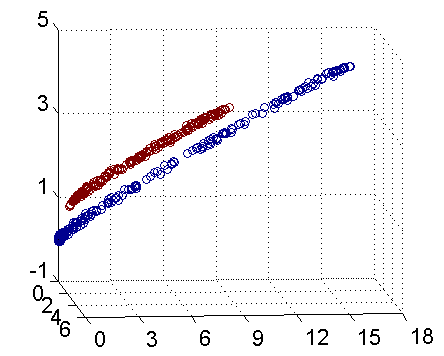
这样通过把二维数据扩展到三维数据就达到了线性可分的目的。不得不说这是核函数表现比较理想的情况，但是这给我们解决线性不可分问题提供了一种解决办法。
目前常用的核函数有
1) 线性核函数
$K(x,z)=<x,z>$
2) 多项式核函数
$K(x,z)=(k_0<x,z>+b_0)^n$
3) 径向基(RBF核)函数
$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})$
4)单极性(sigmoid)核函数
$K(x,z)=tanh(k_0<x,z>+b_0)$

四、软间隔
前面说的都是针对线性可分的数据。现实中遇到的数据大都是线性不可分的。对于线性不可分的数据，可以使用核函数来解决，但是核函数并不一定能够保证升维以后就是线性可分的，因此就有了C-SVC。
C-SVC模型表述如下：
$min\frac{1}{2}||w||^2+C\sum_{i=1}^{m}{\xi_i} \tag{4-1}$
$y_i(w^Tx_i+b)\geq1-\xi_i, i=1,2,...,m\tag{4-2}$
根据与线性可分时同样的对偶方法及KKT条件可以得到对偶形式为：
$max \theta_D(\alpha)=\sum_{i=1}^{m}{\alpha_i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j<x_i,x_j>\tag{4-3}$
约束条件应该为：

$$\begin{Bmatrix} 0\leq \alpha_i\leq C,i=1,2,...,m\\ \sum_{i=1}^{m}\alpha_iy_i=0 \end{Bmatrix}\tag{4-4}$$
除了可以应用到不可分数据外，C-SVM还有一个优点就是对奇异数据的鲁棒性。例如对于线性可分数据，如果移动一个数据到分割面中间的时候，C-SVM分割面的变化程度要大大小于SVM。

五、SMO算法
由于日常的数据大多不可分的，C-SVC已经成为SVM的标准形式，接下来主要讨论怎么使用SMO算法来求解模型(4-3,4)里面的$\alpha_i$。注意到随机梯度上升法在求解最优值的时候的高效，SMO使用随机梯度上升法求解$\alpha_i$。
在迭代的过程中，每一次选择一对$\alpha_i$和$\alpha_j$，其它的$\alpha_k$ 在本次梯度上升迭代过程中不做变化。由于公式(4-4)里面$\sum_{i=1}^{m}\alpha_iy_i=0$ 可得
$\alpha_iy_i+\alpha_jy_j=-\sum_{k=1,k\neq i,k\neq j}^{m}\alpha_ky_k=\zeta \tag{5-1}$
结合$0\leq \alpha_i\leq C,0\leq \alpha_j\leq C$

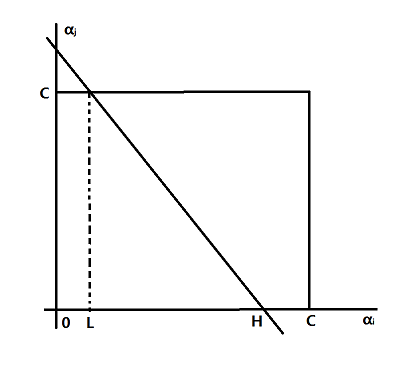
如图所示，可以求解$L\leq \alpha_i\leq H$，接下来只要把公式(4-3,4)里面的$\alpha_j$利用公式(5-1)替换为$\alpha_i$，便很容易求解是的公式(4-3)取最大时的$\alpha_i,\alpha_j$，然后对$\alpha_i,\alpha_j$值进行更新，进入下一次梯度上升过程即可。

参考博客：
1、ML—SVM预热之拉格朗日对偶和KKT条件
http://blog.csdn.net/zhangzhengyi03539/article/details/49366447
2、ML—核技巧
http://blog.csdn.net/zhangzhengyi03539/article/details/49821027