关于函数的学习

函数相关：坐标和坐标系

坐标的实质是有序数对，可以精确地表示一个数

笛卡尔坐标系：二维直角坐标系、三维直角坐标系

笛卡尔~~

“我思故我在”

“越学习，越发现自己的无知”

“怀疑是智慧的源头”

绘图的本质是描点

强推：desmos（滑稽）

强推之二：Calculator Suite - GeoGebra

函数定义

本质上，函数反映了一种映射关系

函数的定义域：自变量的取值范围（自变量所以可取值的集合）

表达符号 一般为：设自变量为x 因变量为y

区间概念！（自变量的取值范围）（[]表示闭区间，（)表示开区间）

2 ≤ x ≤ 10：[ 2 , 10 ]

2 ≤ x < 10：[ 2 , 10 )

2 < x ≤ 10：( 2 , 10 ]

x ≥ 100：[ 100, +∞)

 x ≤ 100: ( -∞ , 100]

研究函数第一条件：研究定义域，接着研究值域（y的取值范围）

一次函数

定义

通常表示为 y = kx + b 的形式 （其中 k 和 b为常数，k ≠ 0）

当 b = 0 时，该式子叫做正比例函数（它是一种特殊的一次函数）

例如 y = x ; y = 2x.

例如，y = x ^ 2 + 100 和 y = 2 / x +100 都不是一个一次函数

一次函数特质

①倾斜度由k(系数)决定

②左右、上去平移跟 b 的值有关  ( 左加右减 ) ( 上加下减 )

下列函数经过怎样的移动得到对应的函数

y = (1)x - 6 -----> y = x - 4 （上2，左2）| - 6 - ( - 4 )  | / 1 = 2

y = 2x - 2 -----------> y = 2x + 4（上6，左3）| - 2 - 4 | / 2 = 3

y = 2x + 4 -----------> y = 2x（上6，左2）|4 - 0 | / 2 = 2 

补充题目

题目1：

参考答案：1. m = 2 ,  n ≠ -1

2. 右（下） 2（ | - 2 | / 1 (系数) = 2）

3. b = 1

4. m = -1

5.  k = 5 , b = -11

1. (y2-y1)/(x2-x1)=k=-2,b=5,表达式：y=-2x+5;

2.(y2-y1)/(x2-x1)=k=3,b=0,表达式：y=3x

3. 先算在y轴上的位置（x= 0）,y1=3,y2=-1,它们的交点y坐标和x坐标相同，所以得到

-2/3x+3=2x-1，解的x=1.5;

∴S▲=4*1.5/2=3;

二次函数

定义

一次函数：y = kx + b(k≠0,x的指数最高是1)

二次函数：y = kx^2+bx+c(k≠0,x最高指数2)

y = ax^2(a≠0)

特质

a>0,开口向上；a<0,开口向下

如图

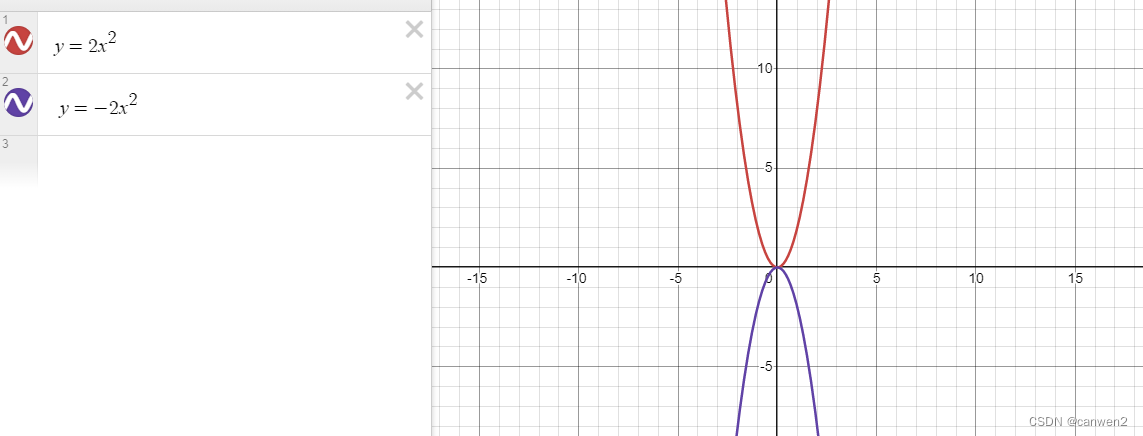
|a|越大，开口越窄；反之，越大 

如图

二次函数图像是对称的

(左边随着x的增大而下降，右边随着x的增大而上升)

( a ± b ) ^ 2  =  a ^ 2 + b ^ 2 ± 2 ab 

y = (x-h)^2 <-------------------------------------------> y = x^2-2hx+h^2

顶点式：

!!

当a>0,x<h,y随着x的增大而减小（如图中绿色的部分）

当a>0,x>h,y随着x的增大而增大（如图中红色的部分）

当a<0,x<h，y随着x的增大而增大（如下图蓝色的部分）

当a<0,x>h, y随着x的增大而増小（如下图红色的部分）

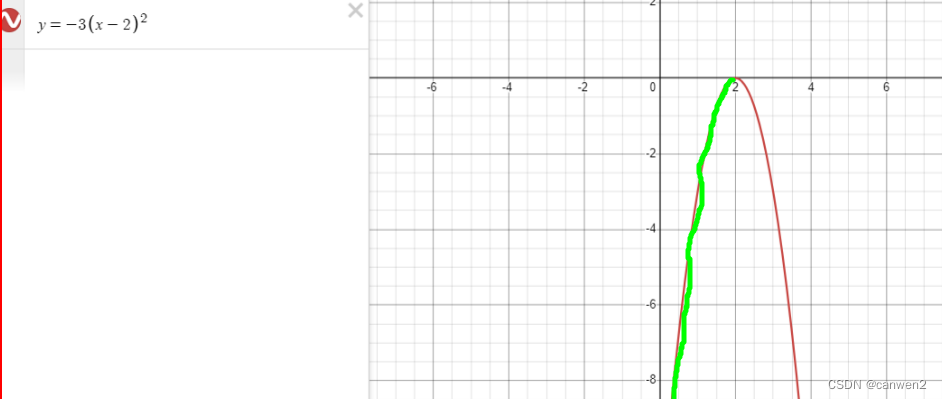
二次函数：对称性、单调性（单调递增、单调递减）（就是x的值不同，y的值也不同）

二次函数vs一次函数

二次函数的增长速度更快、阶更高

指数函数

定义

指数是幂运算的a^m(a≠0)中的一个参数，a为底数，m为指数。叫做a的m次幂，也叫做a的m次方

当m=2，成平方，m=3，成立方

a^0 = 1 (a≠0)

常用的指数与幂运算

a^m * a^n  = a ^ (m+n)

a^m / a^n = a ^ (m-n)

(a^m)^n = a^(m*n)

(ab)^n  = a^n * b^n

根式

一般地，如果x^n = a,那么x叫做a的n次方根，其中n>1，且n∈N

如果一个数的平方等于a，则这个数叫做a的平方根

2，-2叫做4的平方根

如果一个数的立方等于a，则这个数叫做a的立方根

-2是-8的立方根，2是8的立方根

小总结：

2^n = a ，2是a的n次方根 

x^n = a，那么x是a的n次方根 

正数的分数指数幂

规定

指数函数

定义

一次函数：y=kx+b(k≠0)

二次函数：y=ax^2+bx+c(a≠0)

指数函数：y=a^x(a>0,a≠1)（下面是原因（为什么是不属于指数函数）

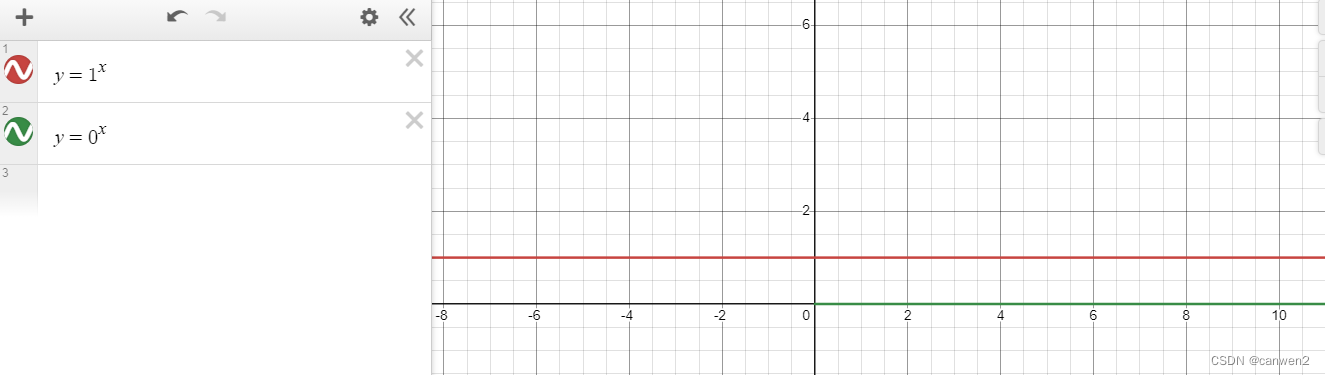
指数增长图像

上图可以打一个形象的比方：你爸有一万块钱，银行利息每年0.05

红线，每次都用当前的数量*(1+0.05)，n年后就是1*(1+0.05)^n次方了，40年就已经有40万左右了！

再比如黑线，国王放旗子的那个例子（指数爆炸）（2^x）

小总结

y=a^x

0<a<1，y随x的增大而减小

0>1，y随x的增大而增大

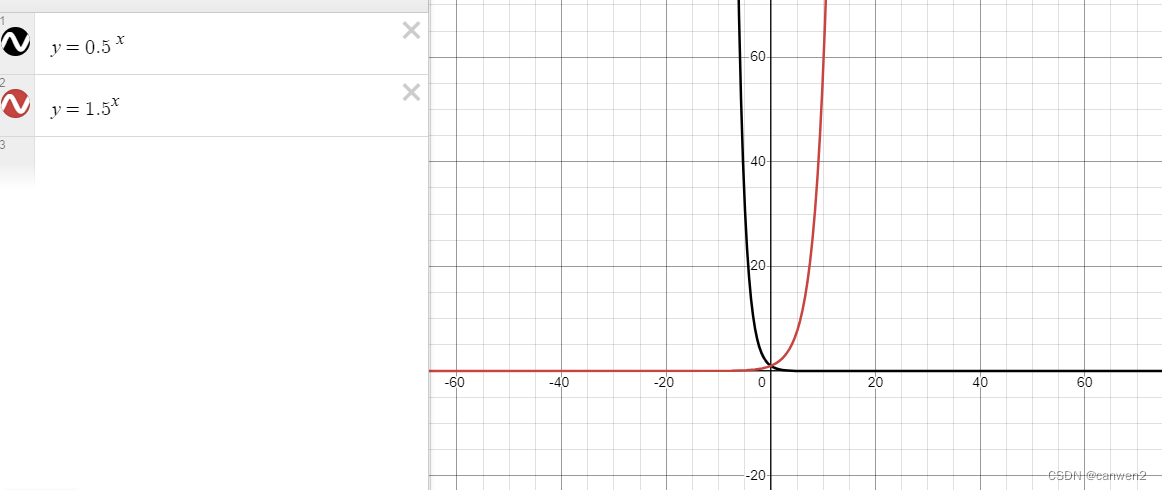
指数函数VS二次函数

所以指数函数增长的比二次函数快

对数函数

定义

a^m =  n (a>0)

定义

2^3 = 8 就说 3 = log2 8 = 3

性质

题目：

log6 3+log 6 2  = log 6(2*3) = 1

log3 3^1024 = 1024* log3 3 = 1024

函数图像

换底公式

我是初中生还不大懂（强推

换底公式_哔哩哔哩_bilibili

各种函数之间的比较

2^x > x^2 > x > log_2x（越往右越快）