Matlap系统稳定性分析【自动控制】

FreeFlowDev

于 2025-03-20 18:49:16 发布

阅读量1k

点赞数 25

文章标签：自动控制理论

本文链接：https://blog.csdn.net/2201_75436278/article/details/146361747

版权

摘要

本报告围绕控制系统的稳定性分析展开，介绍了几种常见的稳定性判据，包括极点分析法、Nyquist判据、Bode图分析、根轨迹法和Lyapunov稳定性理论。通过Matlab仿真，对不同方法进行了验证，分析了系统的极点变化、频率响应及其对系统稳定性的影响。实验结果表明，各种稳定性判据在不同应用场景下各有优劣，其中根轨迹法能够直观地展示增益变化对系统极点的影响，而Lyapunov稳定性理论适用于非线性系统的稳定性判定。

关键词：系统稳定性、极点分析、Nyquist判据、Bode图、根轨迹法、Lyapunov稳定性

1 引言

在现代控制工程中，系统的稳定性是衡量其性能的关键指标之一。稳定性分析不仅影响系统的可靠性，还决定了系统能否在外部扰动下保持预期的动态行为。随着自动化和智能控制技术的发展，工程师需要借助数学方法和计算机仿真来分析和优化系统的稳定性。本报告旨在介绍几种常见的稳定性分析方法，包括极点分析法、Nyquist判据、Bode图分析、根轨迹法和Lyapunov稳定性理论，并利用Matlab进行仿真实验，以比较不同方法的特点和适用场景。希望通过本研究，为读者提供系统稳定性分析的理论基础和实践指导。

2 系统稳定性分析理论基础

2.1 系统稳定性定义

系统稳定性是指系统在初始状态或外部扰动作用下，其时间响应随时间推移逐渐衰减并趋向于零（即回到平衡位置）的能力。如果系统能够回到平衡位置，则称系统是稳定的；如果系统偏离平衡位置越来越远，则称系统是不稳定的。

系统稳定性是系统正常运行的必要条件。一个不稳定的系统无法正常工作，甚至可能导致系统崩溃或数据丢失，这对依赖系统运行的业务和设备来说是不可接受的。通过分析系统的稳定性，可以预测和避免潜在的系统故障，从而提高系统的可靠性。同时，稳定性分析可以帮助工程师了解系统在不同条件下的性能表现，从而进行针对性的系统性能优化。如今，绝大多数工厂都实现了模块化、系统化生产，例如小米工厂，全自动化生产的背后依靠一个稳定的系统支撑。稳定性分析是保障系统安全、正常运行的基础，因此，稳定性分析是很有必要的。‌

2.2 稳定性判据

系统稳定的条件：

从时域上来看，系统的稳定性取决于，当 t 趋于无穷时，系统输出收敛，则认为该系统是稳定的。

一个线性控制系统稳定的条件是：系统的特征方程的所有根都具有负实部，也就是说，这些根都位于复平面的左侧。换句话说，系统的闭环传递函数的极点必须全部位于左半 s 平面内。对于线性连续系统，如果所有特征根（极点）的实部为负，系统就是稳定的；如果特征根的实部为零，系统处于临界稳定状态；而如果特征根（极点）的实部为正，系统则是不稳定的。

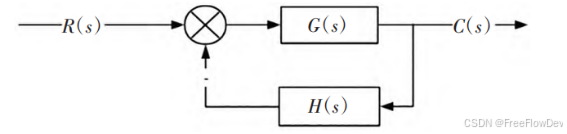
该闭环系统的传递函数为：

$\begin{array} {ccc}\emptyset & (s) & =\frac{\mathrm{G}(s)}{1+\mathrm{G}(s)\mathrm{H}(s)} \end{array}$

则其特征方程为：

$\begin{array} {ccc}\varphi & (s) & =1+\mathrm{G}(s)\mathrm{H}(s) \end{array}$

其稳定性判据都是建立在特征方程上进行的。

3 极点分析法

可以直接将 $\varphi (s)$ 变形转化成以下形式：

$\varphi (s) = (s-r_{1})(s-r_{2})(s-r_{3}) \cdots \cdots$

则该系统的极点为 $r_{1}r_{2} r_{3}\cdots \cdots$

若极点实部全为负数，系统就是稳定的；如果实部为零，则是临界稳定状态；若实部为正，系统就是不稳定的；

以下面这个开环传递函数为例：

$G(s)=\frac{1}{s(s+1)(s+2)(s+3)(s+4)}$

闭环传递函数：

$T(s)=\frac{G(s)}{1+G(s)}=\frac{1}{s(s+1)(s+2)(s+3)(s+4)+1}$

Matlap实现：

num = [1]; % 开环传递函数分子
den = [1 10 35 50 24 0]; % 开环传递函数分母
% 闭环传递函数分母
closed_loop_den = den + [0 0 0 0 0 1]; % 1 + G(s)
% 计算闭环极点
closed_loop_poles = roots(closed_loop_den);
% 显示闭环极点
disp('闭环系统的极点为：');
disp(closed_loop_poles);
% 判断稳定性
if all(real(closed_loop_poles) < 0)
disp('系统是稳定的。');
else
disp('系统是不稳定的。');
end

输出结果:

4 Nyquist稳定性判据

Nyquist稳定性判据的基本思想是：对于一个闭环控制系统，如果开环传递函数在右半s平面没有极点，那么闭环系统稳定的充分必要条件是Nyquist图不包围复平面上的(-1, j0)点；如果开环传递函数在右半s平面有极点，那么闭环系统稳定的充分必要条件是Nyquist图逆时针方向包围(-1, j0)点的次数等于开环传递函数在右半s平面的极点数。因此，我们可以利用Matlap画出Nyquist曲线进行系统稳定性判断。

num = [1]; % 开环传递函数分子
den = [1 10 35 50 24 0];
% 绘制 Nyquist 图
figure;
nyquist(num, den);
title('Nyquist 图');
 
% 计算开环传递函数在右半 s 平面的极点数
open_loop_poles = roots(den);
right_half_plane_poles = sum(real(open_loop_poles) > 0);
disp(['开环传递函数在右半 s 平面的极点数为：', num2str(right_half_plane_poles)]);
 
disp('请观察 Nyquist 图是否包围 (-1, j0) 点：');
if right_half_plane_poles == 0
    disp('如果 Nyquist 图不包围 (-1, j0) 点，则系统稳定。');
else
    disp('如果 Nyquist 图逆时针包围 (-1, j0) 点的次数等于右半 s 平面开环极点数，则系统稳定。');
end

判断稳定性：如果 Nyquist 图逆时针包围 (-1, j0) 点的次数等于右半 s 平面开环极点数，则系统稳定。

5 Bode 图与相位裕度、增益裕度

Bode 图与相位裕度、增益裕度是频域分析中用于判断系统稳定性的重要工具。Bode 图由幅频特性图和相频特性图组成，分别展示系统增益和相位随频率的变化。相位裕度（PM）是指在增益交界频率（ $\omega _{cp}$ ）处，系统相位与 -180° 的差值，用于衡量系统的相对稳定性；增益裕度（GM）是指在相位交界频率（ $\omega _{cg}$ ）处，系统增益与 0 dB 的差值，用于衡量系统的绝对稳定性。通过分析 Bode 图中的相位裕度和增益裕度，可以判断系统是否稳定及其稳定程度：相位裕度越大，系统相对稳定性越好；增益裕度越大，系统抗干扰能力越强。

% 绘制 Bode 图
sys = tf(num, den);
figure;
bode(sys);
title('Bode 图');
 
% 计算相位裕度和增益裕度
[Gm, Pm, Wcg, Wcp] = margin(sys);
 
% 显示结果
disp(['增益裕度 (Gm) = ', num2str(20*log10(Gm)), ' dB']);
disp(['相位裕度 (Pm) = ', num2str(Pm), ' 度']);
disp(['增益交界频率 (Wcg) = ', num2str(Wcg), ' rad/s']);
disp(['相位交界频率 (Wcp) = ', num2str(Wcp), ' rad/s']);

增益裕度 (Gm) = 29.5681 dB

相位裕度 (Pm) = 85.0348 度

增益交界频率 (Wcg) = 0.83648 rad/s

相位交界频率 (Wcp) = 0.04161 rad/s

6 根轨迹法

它研究系统闭环极点如何随着增益K变化而移动，以确定系统的稳定性和动态特性。通过绘制特征方程 $1+\mathrm{KG}(\mathrm{s})=0$ 的根随K变化的轨迹，可以直观判断系统在不同增益下的极点分布，从而调整控制参数，使系统满足稳定性和性能要求。

% 绘制根轨迹图
figure;
rlocus(sys);
title('根轨迹图');
 
% 计算根轨迹的增益和极点
[K, poles] = rlocfind(sys);
 
% 显示结果
disp('选择的增益 K = ');
disp(K);
disp('对应的极点 = ');
disp(poles);

7 Lyapunov稳定性理论

Lyapunov稳定性理论是一种研究非线性系统稳定性的数学方法，它不依赖系统的显式解，而是通过构造 Lyapunov 函数（类似于能量函数）来判断系统的稳定性。如果存在一个适当的 Lyapunov 函数，使其随时间单调递减，则系统是渐进稳定的；如果 Lyapunov 函数恒为正且不会增加，则系统是李雅普诺夫稳定的。该理论广泛应用于非线性控制、鲁棒控制和动力系统分析中。

% 将传递函数转换为状态空间模型
[A, B, C, D] = tf2ss(num, den);
 
% 显示状态空间矩阵
disp('状态矩阵 A = ');
disp(A);
disp('输入矩阵 B = ');
disp(B);
disp('输出矩阵 C = ');
disp(C);
disp('直接传递矩阵 D = ');
disp(D);
 
% 定义正定矩阵 Q
Q = eye(size(A)); % 单位矩阵
 
% 求解 Lyapunov 方程 A^T P + P A = -Q
P = lyap(A', Q);
 
% 检查 P 是否正定
eigenvalues = eig(P);
if all(eigenvalues > 0)
    disp('P 是正定矩阵，系统是稳定的。');
else
    disp('P 不是正定矩阵，系统不稳定。');
end
 
% 显示结果
disp('Lyapunov 方程的解 P = ');
disp(P);
disp('P 的特征值 = ');
disp(eigenvalues);