数学思维练习一：付钱问题

题目描述

几个人一起出去吃饭是常有的事。但在结帐的时候，常常会出现一些争执。

现在有 n 个人出去吃饭，他们总共消费了 S 元。其中第 i 个人带了ai元。幸运的是，所有人带的钱的总数是足够付账的，但现在问题来了：每个人分别要出多少钱呢？

为了公平起见，我们希望在总付钱量恰好为 S 的前提下，最后每个人付的钱的标准差最小。这里我们约定，每个人支付的钱数可以是任意非负实数，即可以不是 1 分钱的整数倍。你需要输出最小的标准差是多少。

标准差的介绍：标准差是多个数与它们平均数差值的平方平均数，一般用于刻画这些数之间的"偏差有多大"。形式化地说，设第 i 个人付的钱为 bi 元，那么标准差为 :

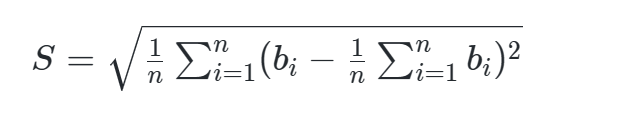
输入描述

第一行包含两个整数 n、S；

第二行包含 n 个非负整数 a1 ⋯, an。

其中，n≤5×10^5,0≤ai≤10^9 。

输出描述

输出最小的标准差，四舍五入保留 4 位小数。

保证正确答案在加上或减去 10−910−9 后不会导致四舍五入的结果发生变化。

输入输出样例

示例

输入

5 2333
666 666 666 666 666

输出

0.0000

运行限制

• 最大运行时间：1s

• 最大运行内存: 256M

思考：

1. 如何保证标准差最小，其实就是使每个人出的钱离平均值的差值小

2. 利用二分的思想，但是我任然有疑惑为什么只需要分两次

3. 通过假设人完全一样，来求刚开始的平均值（这个我也不是很清楚地知道原因）

4. 罗老师的代码是通过反向思维来思考的，通过计算某个钱数*个数看下能不能>=总数，如果小于，那么这个数是小于平均数的，反之大于，以及通过s=s-a[i]来改变总数，保证这个条件可以判断

（图片来自蓝桥杯罗永军老师的PPT）.

实际上就是有一部分人的钱要全出，有一部分的不需要

代码实现：

#include<stdio.h>
#include<stdlib.h>
#include<math.h> 
int compare(const void *a,const void *b)
{
    return *(int *)a-*(int *)b;
}
int main()
{
    int n,s,i;
    double sum=0.0;//这个sum求的是方差 
    scanf("%d%d",&n,&s);
    int a[n];
    for(i=0;i<n;i++)
       {
           scanf("%d",&a[i]);
       }
    int size=sizeof(a)/sizeof(a[0]);
    qsort(a,size,sizeof(a[0]),compare);
    double ave=1.0*s/n;
    for(i=0;i<n;i++)
       {                                 //if和else同时也划分了前半段和后半段 
           if(a[i]*(n-i)<s)
             {
                 sum=sum+(a[i]-ave)*(a[i]-ave);
                 s=s-a[i];
           }
        else
          {
              double nave=s*1.0/(n-i);                  //注意：这里的i是新加过的，这个是新的平均数,用小数保证精度不会丢失,而且个数要改变，前面的人全出，后面的人肯定都是出得起的 
              sum+=(nave-ave)*(nave-ave)*(n-i); 
              break;       //记得要break；出来，现在的结果是对的
               
          }
       }
    printf("%.4lf",sqrt(sum/4));
    
}