地震正演基础理论学习（一）

最新推荐文章于 2025-03-06 12:59:43 发布

都不懂的小白

最新推荐文章于 2025-03-06 12:59:43 发布

阅读量2.2k

点赞数 31

文章标签：学习

本文链接：https://blog.csdn.net/2201_75616815/article/details/143014591

版权

一、概述

地震正演模拟在地震勘探和地震学研究中扮演着重要角色。它通过数学与物理模型，模拟地震波在地下介质中的传播过程，为理解和解释地震数据提供理论基础。本文将深入探讨地震正演的基础理论，包括地震波的基本概念、正演原理、波动方程的求解方法、地震模型的建立等。

二、地震波的基本概念

地震波是地震事件发生后在地壳中传播的能量，主要分为以下几种类型。

2.1 纵波（P波）

性质：纵波是波能量沿介质传播时，使介质的粒子在波前进方向上发生前后振动，因而称为压缩波。P波传播速度最快，是所有地震波中第一个到达地震监测站的波。
传播介质：P波能够在固体、液体甚至气体中传播。当波穿过不同介质的分界面时，会发生折射和反射，影响震源与接收器之间的波形。
数学表示：其传播速度 $v$ 可由介质的弹性模量 $E$ 和密度 $\rho$ 计算，公式为： $v_{P}=\sqrt{\frac{E}{\rho}}$

2.2 横波（S波）

性质：横波是使介质的粒子在波传播方向垂直振动的波，因而称为剪切波。S波传播速度低于P波，并且只能在固体介质中传播。
传播特点：S波的传播会导致介质产生较大的剪切应变，通常造成震后的地面晃动。S波是地震波中造成地表破坏的主要成因之一。
数学表示：S波的传播速度同样可与介质的剪切模量 G和密度 ρ 相关，公式为：
$v_{P}=\sqrt{\frac{E}{\rho}}v_{S}=\sqrt{\frac{G}{\rho}}$

2.3 面波

性质：面波在地表传播，可分为瑞利波和勒夫波。瑞利波的运动特性如同水波，质点呈椭圆轨迹振动，速度介于P波和S波之间。勒夫波则是一种较快的水平面波。
应用：面波通常造成的震感更强，能量衰减较慢，因此在地震的烈度评估中具有重要意义。

三. 地震正演的基本原理

地震正演的核心在于通过数学模型来模拟震源释放的能量如何在地壳中传播，然后生成合成的地震记录，以此帮助解释和理解实测数据。

3.1 波动方程

波动方程是描述地震波传播的核心方程，主要有以下形式：

一维线性声波方程：

$\frac{\partial^{2} p}{\partial t^{2}}=v^{2} \frac{\partial^{2} p}{\partial x^{2}}$

其中，p 为压力，v 为波速，t为时间，x 为空间坐标。
三维弹性波方程：

$\frac{\partial^{2} p}{\partial t^{2}}=v^{2} \frac{\partial^{2} p}{\partial x^{2}}\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=\nabla \cdot \mathbf{T}$

其中，u是位移矢量，ρ是密度，T 是应力张量。

3.2 正演模拟流程

正演的基本步骤包括：

定义介质模型：决定模型中的不同地质结构，与其对应的速度和密度。
设定震源：选择合适的震源模型，定义震源位置、发震机制等。
求解波动方程：选择合适的数值方法（如有限差分法或有限元法）进行求解。
生成合成地震记录：计算与实际地震监测相似的地震记录。

3.3 离散化弹性波方程

其中速度分量 U、V 和应力分量 R、T、H。

$\rho \frac{U_{i, j}^{k+1}-U_{i, j}^{k}}{\Delta t}=\frac{R_{i+\frac{1}{2}, j}^{k}-R_{i-\frac{1}{2}, j}^{k}}{\Delta x}+\frac{H_{i, j+\frac{1}{2}}^{k}-H_{i, j-\frac{1}{2}}^{k}}{\Delta z}$ （1）

$\rho \frac{U_{i, j}^{k+1}-U_{i, j}^{k}}{\Delta t}=\frac{R_{i+\frac{1}{2}, j}^{k}-R_{i-\frac{1}{2}, j}^{k}}{\Delta x}+\frac{H_{i, j+\frac{1}{2}}^{k}-H_{i, j-\frac{1}{2}}^{k}}{\Delta z}\rho \frac{V_{i, j}^{k+1}-V_{i, j}^{k}}{\Delta t}=\frac{H_{i+\frac{1}{2}, j}^{k}-H_{i-\frac{1}{2}, j}^{k}}{\Delta x}+\frac{T_{i, j+\frac{1}{2}}^{k}-T_{i, j-\frac{1}{2}}^{k}}{\Delta z}$ （2）

$\frac{R_{i, j}^{k+1}-R_{i, j}^{k}}{\Delta t}=c_{11} \frac{U_{i+\frac{1}{2}, j}^{k+1}-U_{i-\frac{1}{2}, j}^{k+1}}{\Delta x}+c_{13} \frac{V_{i, j+\frac{1}{2}}^{k+1}-V_{i, j-\frac{1}{2}}^{k+1}}{\Delta z}$ （3）

$\frac{T_{i, j}^{k+1}-T_{i, j}^{k}}{\Delta t}=c_{13} \frac{U_{i+\frac{1}{2}, j}^{k}-U_{i-\frac{1}{2}, j}^{k+1}}{\Delta x}+c_{33} \frac{V_{i, j+\frac{1}{2}}^{k+1}-V_{i, j-\frac{1}{2}}^{k}}{\Delta z}$ （4）

$\frac{H_{i, j}^{k+1}-H_{i, j}^{k}}{\Delta t}=c_{44} \frac{V_{i+\frac{1}{2}, j}^{k+1}-V_{i-\frac{1}{2}, j}^{k+1}}{\Delta x}+c_{44} \frac{U_{i, j+\frac{1}{2}}^{k+1}-U_{i, j-\frac{1}{2}}^{k+1}}{\Delta z}$ （5）

[1] 描述U 速度分量的时间变化与 R 正应力分量和 H 剪切应力分量在 x 和 z 方向上的梯度之间的关系（变化率）
[2] V 速度分量的时间变化与 H 剪切应力分量和 T 正应力分量在 x 和 z 方向上的梯度之间的关系
[3]描述了 R 正应力分量的时间变化与 U 速度分量在 x 方向和 V 速度分量在 z 方向上的梯度之间的关系
[4]描述了 T 正应力分量的时间变化与 U 速度分量在 x 方向和 V 速度分量在 z 方向上的梯度之间的关系
[5]描述了 H 剪切应力分量的时间变化与 V 速度分量在 x 方向和 U 速度分量在 z 方向上的梯度之间的关系

四、波动方程的求解方法

为实现正演模拟，需要求解波动方程。常用的数值方法包括：

4.1 有限差分法（FDM）

原理：将波动方程的空间导数用差分形式替代，将时间视为离散的序列。对于一维声波方程，可以用如下方式近似：
$p(x, t+\Delta t) \approx p(x, t)+\Delta t \cdot \frac{\partial p}{\partial t}$
实现步骤：
1. 确定网格点及时间步长。
2. 建立波场的时间序列。
3. 利用差分公式更新每个网格点的波场值。

4.2 有限元法（FEM）

原理：将复杂模型分割为多个简单的元素，利用变分法形成一组代数方程进行求解。
优点：
- 能够适应不同形状和边界条件的模型。
- 对非均匀介质和复杂地质结构的模拟效果显著好于有限差分法。

4.3 谱方法

原理：通过傅里叶变换将波动方程从时间域转入频率域求解，适合平直区域和简单几何边界的模拟。
优点：通常在高频数值上具有更高精度，适合高效寻找波动的频率响应。

五. 地震模型的建立

地震模型的建立是正演模拟的关键，要求模型能够真实地反映地下介质的物理特性。

5.1 速度模型

定义：速度模型描述地震波在不同地质条件下的传播速度，通常通过地质勘探数据获得，如钻孔测量或地震反射法。
构建策略：
- 根据已有地质资料、实验数据和理论推导逐层构建速度模型。
- 使用插值方法确定分层间的速度变化，以保证模型的连续性。

5.2 密度模型

定义：描述不同地质层的密度分布，影响波的传播特性及反射特征。
建模方法：
- 分析区域内的岩石特性及其物理性质。
- 采用已知的岩石密度数据构建连续的密度模型。

5.3 震源特性

类型：震源可分为点源、线源和面源等，选择合适的震源模型至关重要。
震源参数：震源的强度、深度、位置及释放机制等参数都会影响地震波的传播特征。

六、程序运行

离散化弹性波方程代码及图像

% 正演编程
%二维各向同性均匀介质弹性波_空间二阶时间二阶
tic % 开始计时
clc % 清空命令窗口
close all % 关闭所有图形窗口
clear all % 清除工作区的所有变量


Endtime=0.3;  %模拟时长
delta_t=0.001;% 时间步长，单位：秒
delta_x=0.004;% 空间步长，单位：千米
delta_z=0.004;
CNX=401; % x 方向的网格数
CNZ=401; % z 方向的网格数
rho=2.0; % 密度
Sx=(CNX+1)/2; % 震源位置的 x 坐标
Sz=(CNZ+1)/2; % 震源位置的 z 坐标
f0=40;% 10~40HZ  震源频率
lambda=3.5; % Lame 参数 lambda
mu=3; % Lame 参数 mu
c11=lambda+2*mu; % 弹性系数 c11
c13=lambda; % 弹性系数 c13
c33=lambda+2*mu;  % 弹性系数 c33
c44=mu; % 弹性系数 c44
%vp=2.32 vs=1.3


Rnow=zeros(CNX,CNZ); % 当前时刻的正应力分量 R
Rnext=zeros(CNX,CNZ);  % 下一个时刻的正应力分量 R
Hnow=zeros(CNX,CNZ);   % 当前时刻的剪切应力分量 H
Hnext=zeros(CNX,CNZ); % 下一个时刻的剪切应力分量 H
Tnow=zeros(CNX,CNZ);  % 当前时刻的正应力分量 T
Tnext=zeros(CNX,CNZ); % 下一个时刻的正应力分量 T
Unow=zeros(CNX,CNZ);  % 当前时刻的 x 方向速度分量 U
Unext=zeros(CNX,CNZ); % 下一个时刻的 x 方向速度分量 U
Vnow=zeros(CNX,CNZ); % 当前时刻的 z 方向速度分量 V
Vnext=zeros(CNX,CNZ); % 下一个时刻的 z 方向速度分量 V


% 主程序
for time=0:delta_t:Endtime  % 时间迭代循环
    % x 和 z 方向上的空间迭代
    for i=2:CNX-1
        for j=2:CNZ-1
             % 计算速度分量的时间变化量 delta_u 和 delta_v
            X1 = Rnow(i+1,j) - Rnow(i,j);
            Y1x = Hnow(i,j) - Hnow(i,j-1);
            Y1z = Hnow(i,j) - Hnow(i-1,j);
            Z1 = Tnow(i,j+1) - Tnow(i,j);
            delta_u = (X1+Y1x)*delta_t/(rho*delta_x);
            Unext(i,j)=Unow(i,j) + delta_u;
            delta_v = (Y1z+Z1)*delta_t/(rho*delta_z);
            Vnext(i,j)=Vnow(i,j) + delta_v;
        end
    end
    % x 和 z 方向上的空间迭代
    for i=2:CNX-1
        for j=2:CNZ-1
            % 计算应力分量的时间变化量 delta_r、delta_tn 和 delta_h
            M1 = Unext(i,j) - Unext(i-1,j);
            Mn1 = Unext(i,j+1) - Unext(i,j);
            N1 = Vnext(i,j) - Vnext(i,j-1);
            Nm1 = Vnext(i+1,j) - Vnext(i,j);
            delta_r = delta_t*(c11*M1+c13*N1)/delta_x;
            Rnext(i,j) = Rnow(i,j) + delta_r;
            delta_tn = delta_t*(c13*M1+c33*N1)/delta_x;
            Tnext(i,j) = Tnow(i,j) + delta_tn;
            delta_h = delta_t*(c44*Mn1+c44*Nm1)/delta_x;
            Hnext(i,j) = Hnow(i,j) + delta_h;
        end
    end

  Unext(Sx,Sz)=Unext(Sx,Sz)-5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
  
  %Uprev=Unow;  %波场更新
  Unow=Unext;
  Vnow=Vnext;
  %Vprev=Vnow;  %波场更新
  Rnow=Rnext;
  %Pprev=Pnow;  %波场更新
  Hnow=Hnext;
  Tnow=Tnext;
end
% max(max(Vnext))
%绘图
surf(Rnow)
shading interp;
fip=fopen('D:\mitchelles\Fimage\elsU1_SD.bin','wb');
fwrite(fip,Unow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsV1_SD.bin','wb');
fwrite(fip,Vnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsH1_SD.bin','wb');
fwrite(fip,Hnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsT1_SD.bin','wb');
fwrite(fip,Tnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsR1_SD.bin','wb');
fwrite(fip,Rnow,'float');
fclose(fip);
view(2);%view(90,90)
colormap(gray);
toc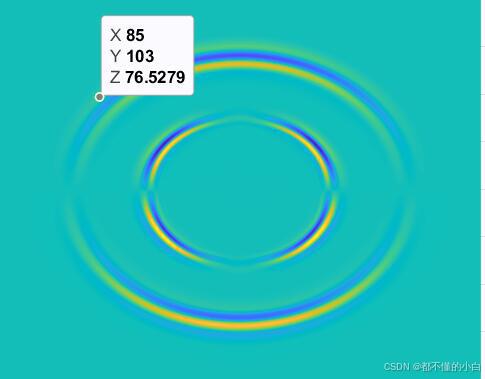

七、总结

P波与S波的主要区别是什么？如何利用这两种波的特性进行地震勘探？

P波与S波的区别：P波（纵波）：传播方向与振动方向一致，可以在固体、液体和气体中传播，速度较快。S波（横波）：传播方向与振动方向垂直，只能在固体中传播，速度较慢。
利用P波和S波进行地震勘探：P波由于速度快，常用于快速初步探测地震的到达时间，帮助确定震源位置。S波由于不能在液体中传播，常用来分析地球内部结构，尤其是地核和地幔的界面。通过对比P波和S波的到达时间差，可以推断出地下介质的性质。

对于新知识掌握的不太熟练和牢固，后期会更加努力加强自己的理论水平。