2.1 随机变量的概念
①离散型:无限可列个→有限个
②非离散型:连续性
2.2.1 离散型随机变量及其概率分布
①X的所有取值(k=1,2,3...)是可列个 X为所有值,x为X的某个具体取值
②{
}
概率函数(分布率) → 图像法,线段总长度为1
性质:
——2023.10.19
2.2.2
连续型随机变量及其概率密度函数
(1)频数直方图
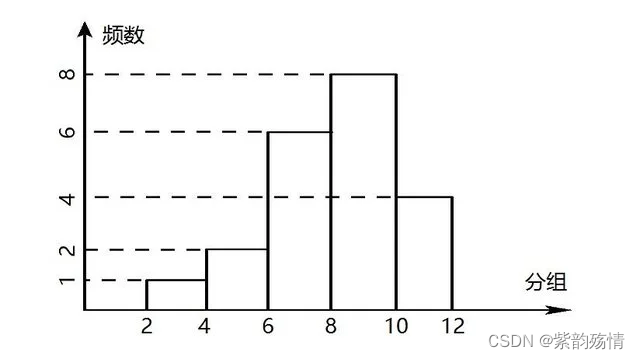
(2)频率密度直方图
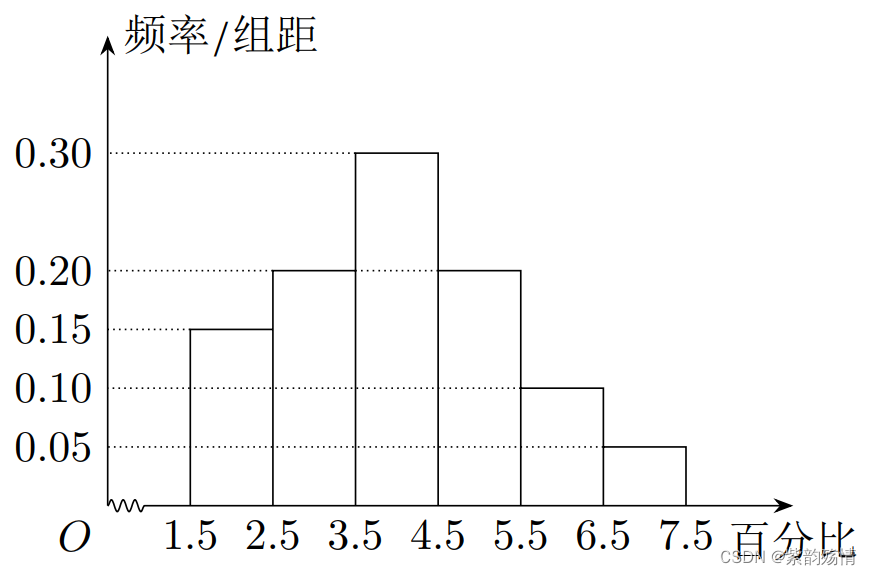
① 每个小长方形的面积=该组的频率
② 所有小长方形面积之和=1
③ 介于x=a,x=b之间的面积,近似于(a,b]之间的频率
概率分布密度函数:
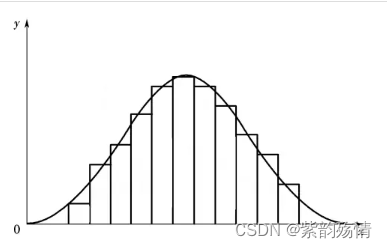
定义
非负可积f(x)≥0,a≤b
x:连续性随机变量 f(x):概率分布密度函数 记作x~f(x)
性质
① f(x)≥0 ② ③ 连续型变量取个别值的概率为0
——2023.10.21
④ 连续型 端点有无不影响概率
⑤ 概率为0未必是不可能事件,概率为1未必是必然事件
分布函数的定义
离散,连续都可用
注:可将+∞和-∞看做概率来计算
性质
(1)
(2)不减,即
(3)F(x)右连续 --> ①离散型,右连续;②连续型,连续
且至多有可列个间断点
离散型分布函数
X取值从小到大排序
分布 —> 概率 间断点是X的取值
连续型分布函数
——2023.10.23
2.2.3
分布公式:
离散型常见分布
① 0-1分布
只有两种实验结果 实验值做一次
② 几何分布
P(A)=P,第k次首次发生,前k-1次未发生
③ 二项分布
P(A)=P,n次实验,发生了k次
注:0-1分布是特殊的二项分布
最值
(1)(n+1)p不为整数,[(n+1)p]达最大值
(2)(n+1)p为整数,(n+1)p,(n+1)p-1达最大值
——2023.10.25
④泊松分布
二项分布 n较大,p较小,np适中 --> 可用泊松分布近似
⑤超几何分布
N个元素:N1属于第一类,N2属于第二类 从中取n个
X:k个属于第一类的个数
不放回抽样试验近似看成放回 --> 二项分布
超几何分布 → 二项分布 → 泊松分布
连续型常见分布
⑥均匀分布
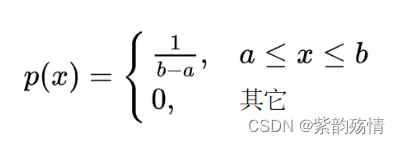
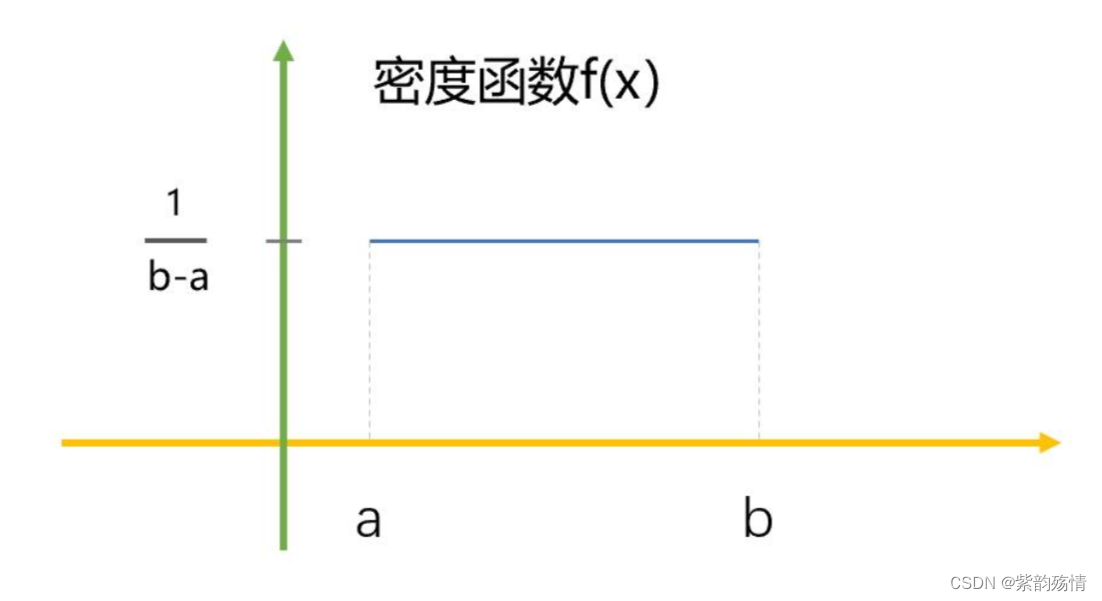
其分布函数为:
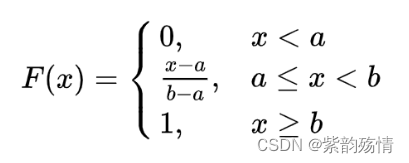
该函数图像为:
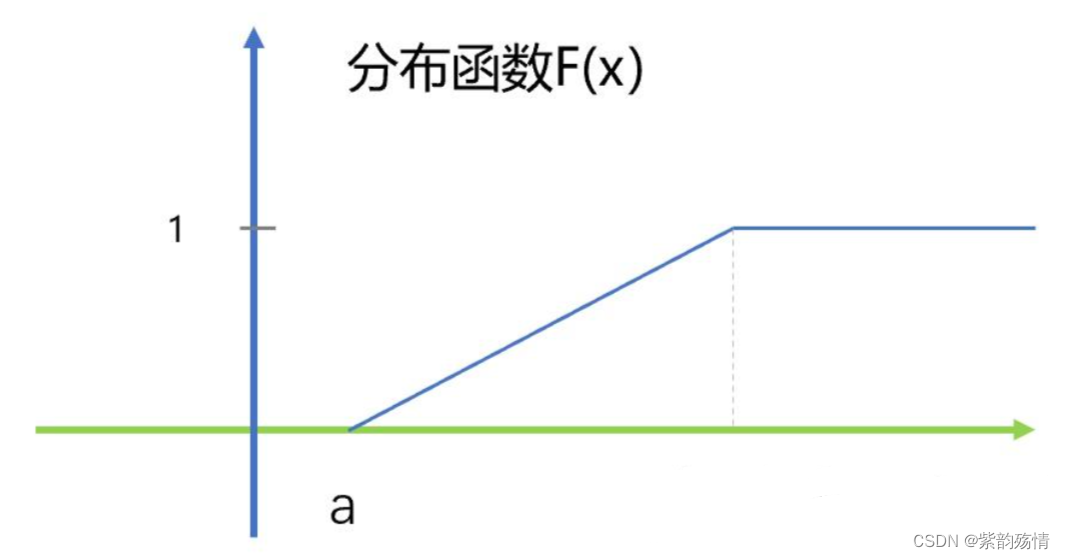
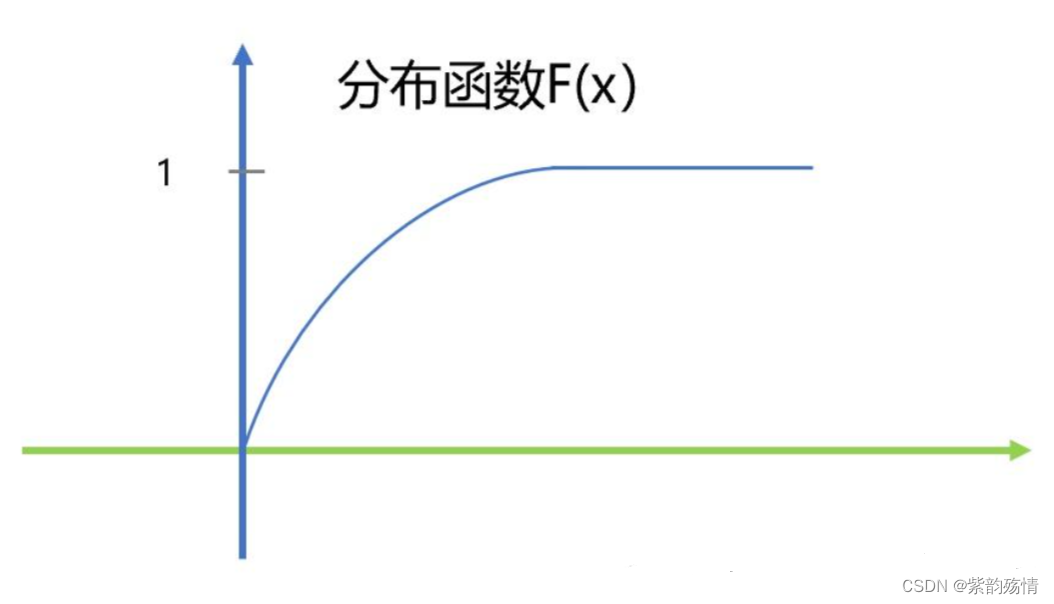
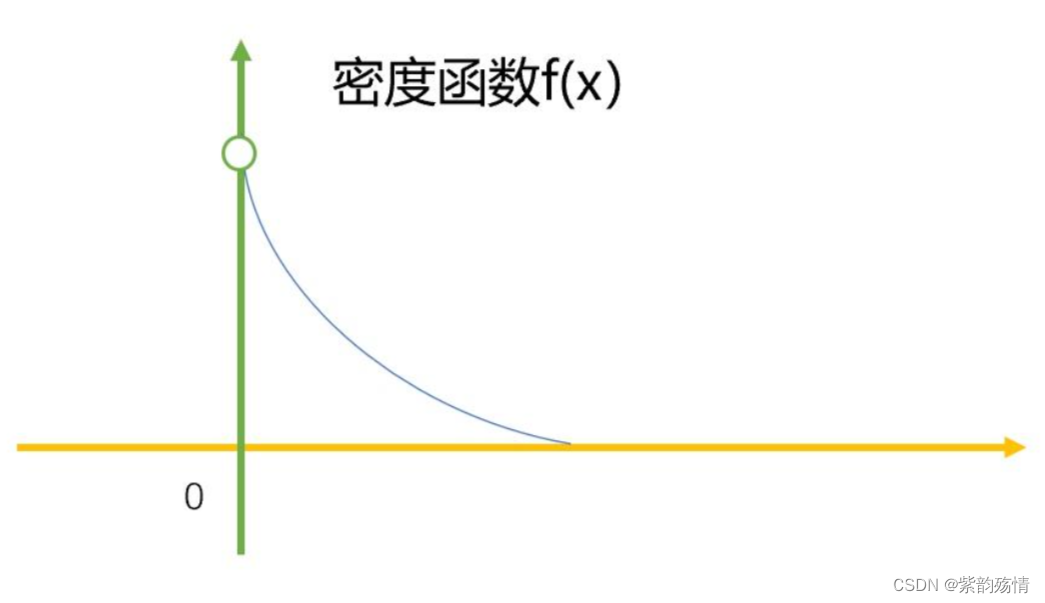
⑦指数分布
其分布函数为:
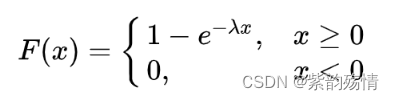
该函数图像为:
——2023.10.26
该分布具有无记忆性,即
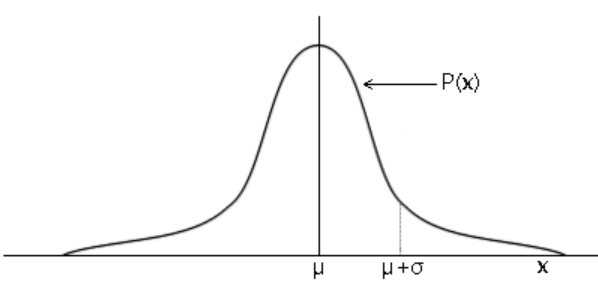
⑧正态分布
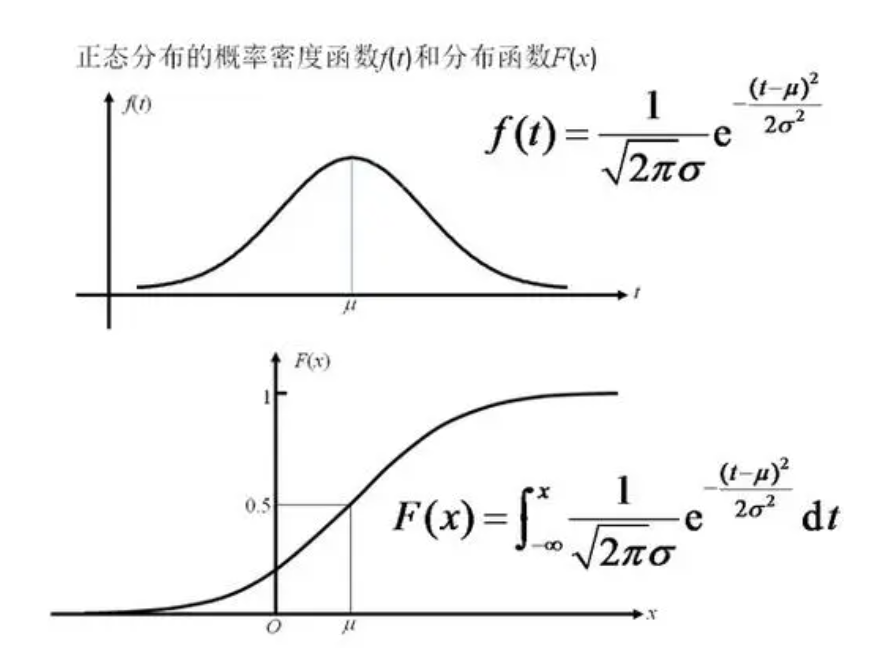
性质
a. 以
为对称轴 钟型
时,
有最大值
b. 以x轴为渐近线 x = μ ± δ 为拐点
d. σ 固定,μ 变化,左右移动
μ 固定,σ 变化,σ ↓,最高点上移 陡
σ ↑,最高点下移 缓
尖峰细尾平峰厚尾
标准正态分布
μ=0,σ=1
性质
y轴为对称轴 --> 偶
——2023.10.30
计算:① 查表
② ,利用函数性质求解
③ ,
④ ,
一般形式转化成标准形式
一般正态分布
3 σ 原则
上 α 分位数
,给定
,找
(点/值)使
2.3.1 随机变量函数的分布(离散型)
变量 --> 已知 函数 --> 构造
若函数值存在相同部分,合并概率
2.3.2 随机变量函数的分布(连续型)
① X服从[a,b]均匀分布,Y=kX+C(K≠0)服从相应区间上的均匀分布
② 正态分布X~N(μ,σ²) Y=aX+b(a≠0)
标准正态分布: ,
③ 定理:X的密度 ,
,则








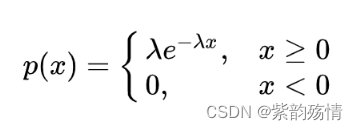














 767
767











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








