灯塔-信号与系统第二章

紫韵殇情

已于 2023-10-23 10:45:52 修改

阅读量96

点赞数

文章标签：信号处理

于 2023-10-20 22:00:00 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/2201_76047120/article/details/133947145

版权

连续LTI系统卷积公式

$y(t)=x(t)\ast h(t)=\int_{-\infty }^{+\infty }x(\tau )h(t-\tau )d\tau$

冲激函数的性质

性质

$1.\int_{-\infty }^{+\infty }\delta (t)dt=1$

$2.\int_{-\infty }^{+\infty }x(t)\delta (t)dt=x(0)$

$\int_{-\infty }^{+\infty }x(t)\delta (t-t_{0})dt=x(t_{0})$

$3.x(t)\delta (t)=x(0)\delta (t)$

$x(t)\delta (t-t_{0})=x(t_{0})\delta (t-t_{0})$

两个函数相等的定义 → 勒贝格

定义1： $f_{1}(t)$ 与 $f_{2}(t)$ 只在有限个点上不相等，其他都相等，则 $f_{1}(t)=f_{2}(t)$ 定义2 ：对任意函数y(t)有：注：y(t)不可以取奇异函数

$\int_{-\infty }^{+\infty }y(t)f_{1}(t)dt=\int_{-\infty }^{+\infty }y(t)f_{2}(t)dt$ （勒贝格定义）

$f_{1}(t)$ 与 $f_{2}(t)$ 只在可数个点上不相等

$4.\delta (at)=\frac{1}{\left | a \right |}\delta (t)$

$\delta (at+b)=\frac{1}{\left | a \right |}\delta (t+\frac{b}{a})$

——2023.10.20

$5.\delta (f(t))=\Sigma \frac{1}{\left | {f}'(t_{0}) \right |}\delta (t-t_{0})$ 所有 $f_{1}(t_{0})=0$

注：4是5的一个特例

定理

$h_{1}(t)=h_{2 }(t)$ ，对 $\forall x(t)$ 都有 $x(t)\ast h_{1}(t)=x(t)\ast h_{2}(t)$

无限集

① 可数无限集（可数集）

$\exists A\leftrightarrow B$ 一一映射，则A与B一样多

若A与B一样多，则称A与B等势或基数相等

② 不可数无限集（不可数集）

δ(t)的多样性

δ(t)的定义

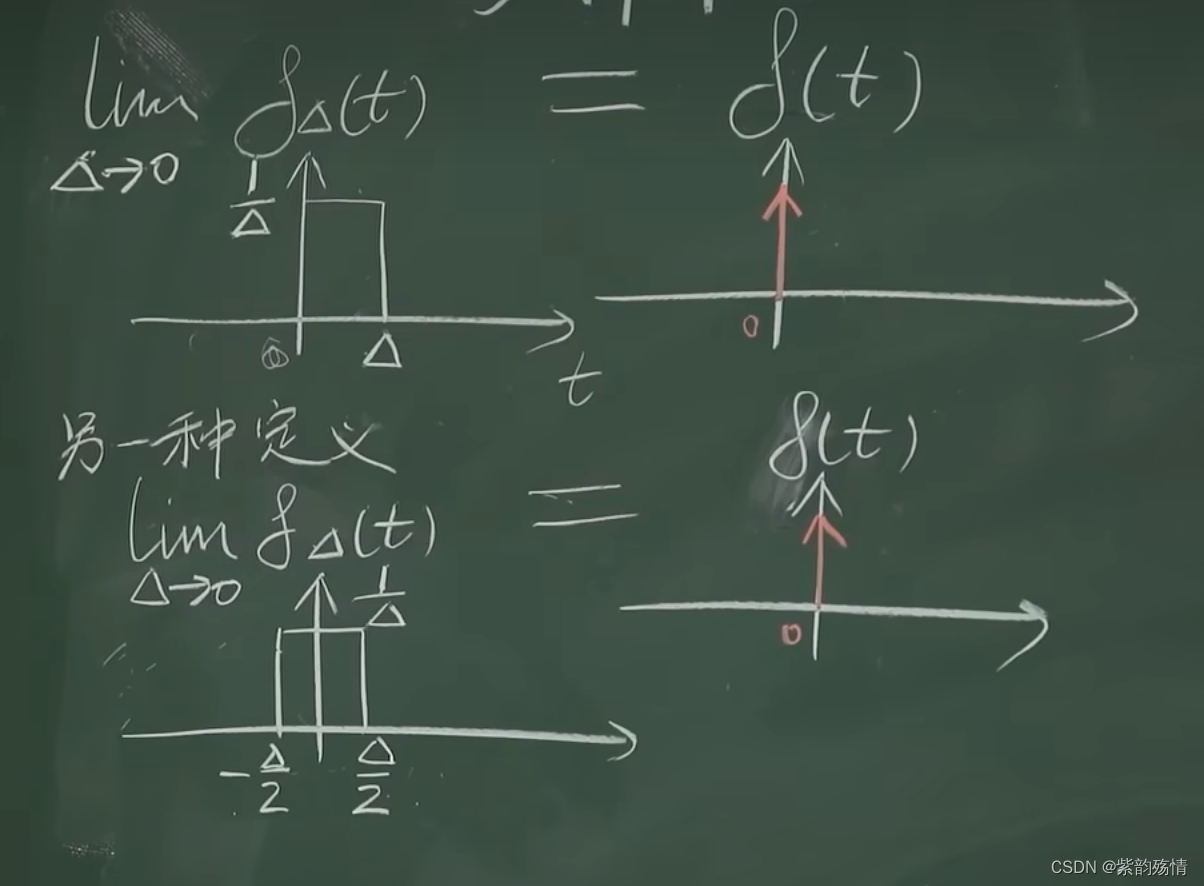
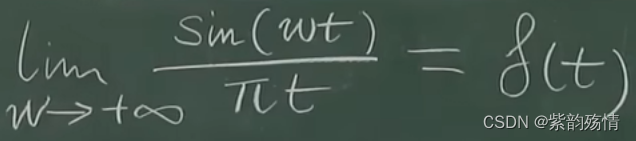
引理

若 $x(t)$ 不是无限振荡函数，则 $\lim_{\omega \to \infty }\int_{-\infty }^{+\infty }x(t)\cos (\omega t)dt=0$

$\lim_{\omega \to \infty }\int_{-\infty }^{+\infty }x(t)\cos (\omega t)dt=0$

连续信号卷积计算

卷积公式： $y(t)=x(t)\ast h(t)=\int_{-\infty }^{+\infty }x(\tau )h(t-\tau )d\tau$

——2023.10.21

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
灯塔-信号与系统第二章

两个函数相等的定义 → 勒贝格。注：y(t)不可以取奇异函数。上不相等，其他都相等，则。
复制链接

扫一扫

紫韵殇情 CSDN认证博客专家 CSDN认证企业博客

码龄2年

14: 原创

134万+: 周排名

22万+: 总排名

1386: 访问

: 等级

164: 积分

16: 粉丝

23: 获赞

7: 评论

15: 收藏

私信

关注

热门文章

分类专栏

概率论与数理统计 1篇
模拟电子技术基础 11篇

最新评论

灯塔-模拟电子技术 4.4
CSDN-Ada助手: 恭喜您写了第13篇博客！您对模拟电子技术的研究和分享让人印象深刻。希望您能继续保持创作的热情，不断探索更多关于灯塔和模拟电子技术的内容。或许可以考虑深入探讨一些实际案例或者应用场景，让读者更加直观地了解这方面的知识。期待您的下一篇作品！
灯塔-模拟电子技术 4.2
CSDN-Ada助手: 恭喜你写了第11篇博客，“灯塔-模拟电子技术 4.2”！你的持续创作让我感到非常欣慰。我希望你可以继续保持写作的热情，同时也建议你在下一篇博客中可以尝试加入一些实例分析或者案例研究，这样可以更好地吸引读者的注意。期待你的下一篇作品！
灯塔-模拟电子技术 4.1
CSDN-Ada助手: 恭喜您第10篇博客的发布！标题“灯塔-模拟电子技术 4.1”让我很期待地点击了进去。您的持续创作真的很令人佩服，我感到非常高兴看到您在电子技术领域的深入探索。在这篇博客中，您似乎探讨了模拟电子技术的一些方面，这无疑是一个重要的主题。您的文章内容涵盖了什么呢？我非常期待了解更多关于模拟电子技术的知识和应用。或许，您可以分享一些实际案例或者提供一些实用的技巧，以帮助读者更好地理解和应用模拟电子技术。总之，我真的很喜欢您的博客。您在电子技术领域的知识和热情让我受益匪浅。希望您能继续保持创作的势头，为我们带来更多有趣且深入的内容。谢谢您的分享！
灯塔-模拟电子技术 2.6
CSDN-Ada助手: 恭喜作者写了第5篇博客，题为“灯塔-模拟电子技术 2.6”。您的博客内容一如既往地精彩，我对您持续创作的热情表示赞赏。在这篇博客中，您对模拟电子技术的介绍非常详细，让我对这个领域有了更深入的了解。在下一步的创作中，我想建议您可以考虑加入一些实例或案例分析，以帮助读者更好地理解模拟电子技术的应用。此外，您可以分享一些您个人的经验或故事，让读者更易于与您的博客产生共鸣。再次恭喜您，期待您未来更多精彩的博客！
灯塔-模拟电子技术 3.3
CSDN-Ada助手: 恭喜您第9篇博客的发表！看到标题《灯塔-模拟电子技术 3.3》，我对您的持续创作精神深感钦佩。您的博客一直都能为读者们带来有趣而富有启发性的内容。在下一步的创作中，我想谦虚地提出一些建议。或许您可以考虑在文章中加入一些实例或案例，以更具体的方式展示模拟电子技术的应用。此外，如果能够分享一些您自己的实践经验或者对于该领域的前沿研究的见解，将会让读者们更深入地了解这个领域的发展动态。再次恭喜您的辛勤努力，期待未来更多精彩的博客文章！

大家在看

最新文章

目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。