主成分分析(Principal Component Analysis, PCA)是一种常用的数据降维技术,其基本原理是通过线性变换将原始数据变换为一组新的正交变量(即主成分),这些新变量是原始变量的线性组合,且具有特定的性质
定义
PCA旨在通过找到数据中的主要成分(方差最大的方向),来减少数据的维度,同时尽量保留数据的信息。通过降维,可以简化数据分析和可视化过程,去除噪声和冗余信息,以及改善模型的性能。
PCA的原理:
数据标准化
在应用PCA之前,通常需要对原始数据进行标准化处理,确保各个特征具有相同的重要性。一般的标准化方法是将每个特征的数据进行零均值化和单位方差化。
协方差矩阵
设有一个包含 ( n ) 个样本和 ( d ) 个特征的数据集,可以构建一个 的协方差矩阵 ,其中元素
表示第 ( i ) 个特征和第 ( j ) 个特征的协方差。协方差矩阵的定义如下:
其中 ( X ) 是一个 的数据矩阵,每行代表一个样本,每列代表一个特征。
特征值分解
对协方差矩阵 进行特征值分解,得到特征值和特征向量。特征值分解可以表示为:
其中 ( V ) 是一个的正交矩阵,其列向量是协方差矩阵的特征向量。
是一个对角矩阵,其对角线上的元素是协方差矩阵的特征值。
选择主成分
按照特征值的大小,选择前 ( k ) 个特征值对应的特征向量作为主成分。这些特征向量构成了新的坐标系的基,即主成分。选择前 ( k ) 个特征值对应的主成分能够最大化保留原始数据中的方差,因此能最大程度地保留数据的信息。
数据投影
通过选取的主成分构成的正交基,将原始的 ( d ) 维数据集投影到一个 ( k ) 维的子空间。数据在新的子空间中的坐标即为主成分分析的结果,称为主成分分数。
解释方差
主成分的特征值表示数据在对应方向上的方差大小。选择较大的特征值对应的主成分,可以保留原始数据中最重要的方差,即最重要的特征信息。
PCA(Principal Component Analysis)的工作流程:
标准化数据
首先对原始数据进行标准化处理,确保每个特征的均值为零,标准差为一。这一步消除了不同特征之间的量纲差异,使得每个特征对PCA的贡献相对均等。标准化后的数据矩阵记为 ( X )。
计算协方差矩阵
使用标准化后的数据矩阵 ( X ),计算其协方差矩阵。协方差矩阵描述了数据中每对特征之间的关系,是PCA分析的数学基础。协方差矩阵的元素 表示第 ( i ) 个和第 ( j ) 个特征之间的协方差。
计算特征值和特征向量
对协方差矩阵进行特征值分解,得到特征值和对应的特征向量矩阵 ( V )。特征值
是一个对角矩阵,其对角线上的元素是协方差矩阵的特征值,特征向量矩阵 ( V ) 的列向量是对应的特征向量。特征值和特征向量满足以下关系:
这一步的目的是找到数据中的主成分,即数据变化最显著的方向。
选择主成分
按照特征值的大小降序排列,选择前 ( k ) 个特征值对应的特征向量作为主成分。选择的主成分数 ( k ) 决定了降维后保留的信息量和数据的维度。
数据投影
构建变换矩阵 ( W ),其列是选择的前 ( k ) 个特征向量。将原始数据矩阵 ( X ) 与变换矩阵 ( W ) 相乘,即 ,得到降维后的数据矩阵。在新的坐标系中,每一行表示一个样本在主成分方向上的投影,实现了数据的降维。
功能实现
导入库和数据准备
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
data = pd.read_csv(r'C:\Users\86187\Desktop\iris.csv')
X = data[['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']]
y = data['Species']数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)StandardScaler 用于将数据集 X 标准化,使得每个特征的均值为0,方差为1,有助于确保每个特征对主成分分析的贡献权重是一致的。
主成分分析(PCA)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)PCA 类通过调用 fit_transform 方法对标准化后的数据 X_scaled 进行主成分分析降维处理。n_components=2 指定了要保留的主成分数量为2,即将数据从原来的四维空间降到二维空间。
可视化PCA结果
fig, ax = plt.subplots()
species = data['Species'].unique()
colors = ['blue', 'orange', 'green']
markers = ['o', '^', 's']
for specie, color, marker in zip(species, colors, markers):
indices = data['Species'] == specie
ax.scatter(X_pca[indices, 0], X_pca[indices, 1], c=color, label=specie, marker=marker)
ax.set_title('PCA of Iris Dataset')
ax.set_xlabel('Principal Component 1')
ax.set_ylabel('Principal Component 2')
ax.legend()
plt.show()创建了一个新的图形 fig 和轴 ax,然后使用 scatter 方法在二维空间中绘制降维后的数据点。for 循环根据鸢尾花的三个不同物种(setosa, versicolor, virginica)分别使用不同的颜色(blue, orange, green)和标记(o, ^, s)来绘制数据点。ax.set_title, ax.set_xlabel, ax.set_ylabel 设置了图表的标题和坐标轴标签。 ax.legend() 添加了图例,展示了每种鸢尾花物种对应的颜色和标记。 plt.show() 显示了最终的PCA降维结果的散点图。
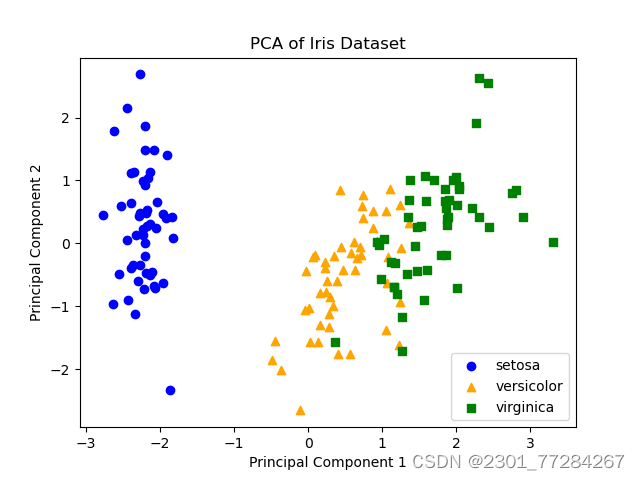
总结
PCA的主要思想是将原始数据映射到一个新的坐标系中,使得数据在新坐标系下的方差最大化,从而实现数据的降维。它在数据预处理、特征提取和可视化等领域有着广泛的应用,是许多机器学习和数据分析任务中不可或缺的工具之一。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








