优化模型——模拟退火算法

每天睡不醒醒醒

已于 2024-09-09 09:50:57 修改

阅读量1.4k

点赞数 21

文章标签： python

于 2024-08-30 10:38:03 首次发布

本文链接：https://blog.csdn.net/2301_77770759/article/details/141688089

版权

物理上的退火

在热力学上，退火（annealing）现象指物体逐渐降温的物理现象，温度降低，物体的能量状态也会降低；在足够低后，液体开始冷凝与结晶。在结晶状态时，系统的能量状态最低。大自然在缓慢降温（退火）时，可形成最低能量状态：结晶。但是，如果降温过程过急过快，快速降温时，会形成不是最低能态的非晶形。

慢工出细活：缓慢降温，使得物体分子在每一温度时，能够有足够时间找到安顿位置，则逐渐地，到最后可能得到最低能态

Metropolis（蒙特卡洛）准则

从当前状态i生成新状态j，若新状态的内能小于状态i的内能（ $eq?E_j%3CE_i$ ），则接受新状态j作为新的当前状态；否则以概率 $eq?exp%5B-%5Cfrac%7B%28E_j%20-%20E_i%7D%7BkT%7D%5D$ 接受状态j，其中 $eq?k$ 为Boltzmann常数。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为 $eq?exp%28-%5Cfrac%7B%5CDelta%20E%7D%7BkT%7D%29$ ，其中E为温度T时的内能， $eq?%5CDelta%20E$ 为其改变数
$eq?p%20%3D%20%5Cbegin%7Bcases%7D%201%20%26%5Ctext%7B%20if%20%24E%28x_%7Bnew%7D%29%3CE%28x_%7Bold%7D%29%24%7D%20%5C%5C%5C%5C%20exp%28-%20%5Cfrac%7BE%28x_%7Bnew%7D%29-E%28x_%7Bold%7D%29%7D%7BT%7D%29%20%26%5Ctext%7Bif%20%24E%28x_%7Bnew%7D%29%20%5Cgeq%20E%28x_%7Bold%7D%29%24%7D%5Cend%7Bcases%7D$

模拟退火

模拟退火算法其实也是一种Greedy贪心算法，但是它的搜索过程引入了随机因素，在迭代更新可行解时，以一定的概率来接受一个比当前解要差的解，因此有可能跳出局部最优解，达到全局最优解。

模拟退火算法模型

基本思想：初始化：初始温度 $eq?T$ ，初始解状态 $eq?S$ ，每个 $eq?T$ 值的迭代数 $eq?L$

第一步：由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

第二步：计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步：判断新解是否被接受，判断的依据是一个接受准则，最常用的接受准则是Metropolis准则: 若Δt′<0则接受S′作为新的当前解S，否则以概率exp(-Δt′/T)接受S′作为新的当前解S4。

第四步：当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。

模拟退火算法与初始值无关，算法求得的解与初始解状态 $eq?S$ (是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率l收敛于全局最优解的全局优化算法；模拟退火算法具有并行性。

参数设置

控制参数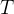 $eq?T$ 的初值 $eq?T_0$ ：

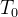模拟退火算法是通过控制参数T的初值 $eq?T_0$ 和气衰减变化过程来实现大范围的粗略搜索与局部的精细搜索。在问题规模较大时，过小的 $eq?T_0$ 往往导致算法难以跳出局部陷阱而达不到全局最优。一般为100℃。初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。

控制参数 T 的衰减函数：

$eq?T_%7Bk+1%7D%3D%5Calpha%20T_k%20%2C%5Ctext%7B%20%24k%20%3D%200%2C1%2C2%2C%5Ccdots%20%2C%20%5Calpha%20%5Cin%20%280%2C1%29%24%7D$

其中， $eq?k$ 为降温的次数， $eq?%5Calpha$ 是一个常数，可以取为0.5~0.99，它的取值决定了降温过程的快慢。为了保证较大的搜索空间， $eq?%5Calpha$ 一般取接近于1的值

退火速度：Markov链的长度

Markov链的选取原则是：在控制参数T的衰减函数已经选定的前提下， $eq?L_k$ 应能使在控制参数 $eq?T$ 的每一取值上达到准平衡从经验上说，可令 $eq?L_k%3D100n$ ， $eq?n$ 为问题规模

控制参数T的终止 $eq?T_f$

算法停止准则：在 $eq?T$ 比较大的高温情况，指数上的分母比较大，而这是一个负指数，所以整个接受函数可能会趋于1，即比当前解 $eq?x_i$ 更差的新解 $eq?x_j$ 也可能被接受因此就有可能跳出局部极小而进行广域搜索，去搜索解空间的其他区域；而随着冷却的进行， $eq?T$ 减小到一个比较小的值时，接收函数分母小了整体也小了，即难于接受比当前解更差的解，也就不太容易跳出当前的区域。如果在高温时，已经进行了充分的广域搜索，找到了可能存在的最好解的区域，而在低温再进行足够的局部搜索，则可能最终找到全局最优 $eq?T_j$ 应设为足够小的正数， $eq?%280.01%2C5%29$

优缺点及改进

　　模拟退火算法（simulated annealing）是一种通用概率算法，用来在一个大的搜寻空间内寻找问题的最优解。

优点：能够有效解决NP难问题、避免陷入局部最优解。

计算过程简单，通用，鲁棒性强，适用于并行处理，可用于求解复杂的非线性优化问题。

模拟退火算法与初始值无关，算法求得的解与初始解状态S(是算法迭代的起点)无关；

模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率收敛于全局最优解的全局优化算法；

模拟退火算法具有并行性

缺点：收敛速度慢，执行时间长，算法性能与初始值有关及参数敏感等缺点。

由于要求较高的初始温度、较慢的降温速率、较低的终止温度，以及各温度下足够多次的抽样，因此优化过程较长。

（1)如果降温过程足够缓慢，多得到的解的性能会比较好，但与此相对的是收敛速度太慢；

（2）如果降温过程过快，很可能得不到全局最优解。

适用环境：组合优化问题。

改进：

　　　　(1)设计合适的状态产生函数

　　　　(2)设计高效的退火策略。

　　　　(3)采用并行搜索结构。

　　　　(4)选择合适的初始状态。

　　　　(5)设计合适的算法终止准则。

　　　　(6)增加升温或重升温过程。在算法进程的适当时机，将温度适当提高，从而可激活各状态的接受概率，以调整搜索进程中的当前状态，避免算法在局部极小解处停滞不前。

　　　　(7)增加补充搜索过程。即在退火过程结束后，以搜索到的最优解为初始状态，再次执行模拟退火过程或局部性搜索。

　　　　(8)对每一当前状态，采用多次搜索策略，以概率接受区域内的最优状态，而非标准SA的单次比较方式。

　　　　(9)结合其他搜索机制的算法，如遗传算法、混沌搜索、粒子群优化等。

通用代码

下面我们举一个简单的例子来呈现python是如何实现模拟退火算法的

已知在优化问题中我们有目标函数和约束条件

（随便给的）

目标函数： $eq?f%28x%29%20%3D%20x%20%5E2%20+%203%20%5Csin%7B5x%7D%20+%202%20%5Ccos%7B4x%7D$

约束条件： $eq?x%20%5Cleq5$

import numpy as np
import matplotlib.pyplot as plt

# 参数设置
initial_temp = 100 # 初始温度
min_temp = 1e-5 # 最小温度
alpha = 0.99 # 温度衰减系数
step_size = 0.5 # 领域步长
max_iter = 10000 # 最大迭代次数

# 目标函数
def objective_function(x):
    return x**2 + 4 * np.sin(5*x) + 2 * np.sin(2*x)

# 搜索解
def neighbour(x, step_size):
    return x + np.random.uniform(-step_size, step_size)

# 约束条件
def is_valid(x):
    if x > 5:
        return False
    
# 模拟退火    
def simulated_annealing(objective_funcion, initial_temp, min_temp, alpha, step_size, max_iter):
    # 初始化解
    current_solution = np.random.uniform(-10, 10)
    current_value = objective_function(current_solution)
    
    # 设置初始温度
    temp = initial_temp
    
    # 保存最优解
    best_solution = current_solution
    best_value = current_value
    
    # 迭代
    for i in range(max_iter):
        # 生成新解
        new_solution = neighbour(current_solution, step_size)
        new_value = objective_function(new_solution)
        
        if is_valid(new_solution) == False:
            continue
        #计算差
        diff_E = new_value - current_value
        
        if diff_E < 0 or np.random.rand() < np.exp(- diff_E / temp):
            current_solution = new_solution
            current_value = new_value
           
        if current_value < best_value:
            best_value = current_value
            best_solution = current_solution
            
        temp *= alpha
        
        if temp < min_temp:
            break
     
    return best_solution, best_value
    
best_solution, best_value = simulated_annealing(objective_function, initial_temp, min_temp, alpha, step_size, max_iter)

print(best_solution, best_value)

绘制过程图

如果想要呈现出模拟退火算法的过程，只需记录下每次迭代的当前解、目标函数值以及温度即可

初始化

solutions = []
values = []
temperatures = []

在循环中加入

# 记录当前解、目标函数值和温度
solutions.append(current_solution)
values.append(current_value)
temperatures.append(temp)

最后在末尾加入

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

# 绘制分开的图表
plt.figure(figsize=(12, 6))

# 绘制解的变化
plt.subplot(1, 2, 1)
plt.plot(solutions, label='解')
plt.xlabel('迭代次数')
plt.ylabel('解')
plt.title('解的变化')
plt.grid(True)
plt.legend()

# 绘制目标函数值的变化
plt.subplot(1, 2, 2)
plt.plot(values, label='目标函数值', color='orange')
plt.xlabel('迭代次数')
plt.ylabel('目标函数值')
plt.title('目标函数的变化')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

# 绘制解的变化和目标函数值的变化在同一个图上
plt.figure(figsize=(10, 6))

# 使用双y轴
fig, ax1 = plt.subplots()

color = 'tab:blue'
ax1.set_xlabel('迭代次数')
ax1.set_ylabel('解', color=color)
ax1.plot(solutions, color=color, label='解')
ax1.tick_params(axis='y', labelcolor=color)

ax2 = ax1.twinx()  # 实例化第二个y轴共享同一个x轴
color = 'tab:orange'
ax2.set_ylabel('目标函数值', color=color)
ax2.plot(values, color=color, label='目标函数值')
ax2.tick_params(axis='y', labelcolor=color)

fig.tight_layout()  # 自动调整图像以适应布局
plt.title('模拟退火过程图')
plt.show()

一些改进策略

多启动

字面意思，即重复多次模拟退火过程，记下每次的最优解，从而得到整体的最优解

动态调整Markov链的长度

# 每100次迭代减小步长
if i % 100 == 0:
	step_size = max(0.1, step_size * 0.9)

混合搜索

在模拟退火的初期进行全局探索时，可以使用遗传算法或粒子群优化等生成初始解；在中后期，结合局部搜索精细优化解

# 使用遗传算法得到初始解
current_solution, current_value = genetic_algorithm_search(population, objective_function, num_generations=50, step_size=step_size)

# 在特定阶段使用遗传算法进行补充搜索
if i % 500 == 0 and i > 0:
    population = [neighbour(current_solution, step_size) for _ in range(20)]
    best_solution, best_value = genetic_algorithm_search(population, objective_function, num_generations=50, step_size=step_size)
    current_solution, current_value = best_solution, best_value

增加补充搜索过程

每进行一定的迭代次数，我们便进行局部搜索，从而更好地获得全局最优解

# 局部搜索
def local_search(current_solution, objective_function, step_size, max_local_iter=10):
    best_local_solution = current_solution
    best_local_value = objective_function(current_solution)
    
    for _ in range(max_local_iter):
        new_solution = neighbour(best_local_solution, step_size)
        new_value = objective_function(new_solution)
        if new_value < best_local_value:
            best_local_solution = new_solution
            best_local_value = new_value
    
    return best_local_solution, best_local_value

if i % 100 == 0:  # 每隔一定的迭代次数进行局部搜索
    current_solution, current_value = local_search(current_solution, objective_function, step_size)