深度学习的两大问题概述——分类和回归

最新推荐文章于 2025-03-17 14:47:32 发布

逸芊

最新推荐文章于 2025-03-17 14:47:32 发布

阅读量2.3k

点赞数 18

文章标签：分类回归深度学习

本文链接：https://blog.csdn.net/2301_78829965/article/details/141341872

版权

一、分类和回归的本质区别

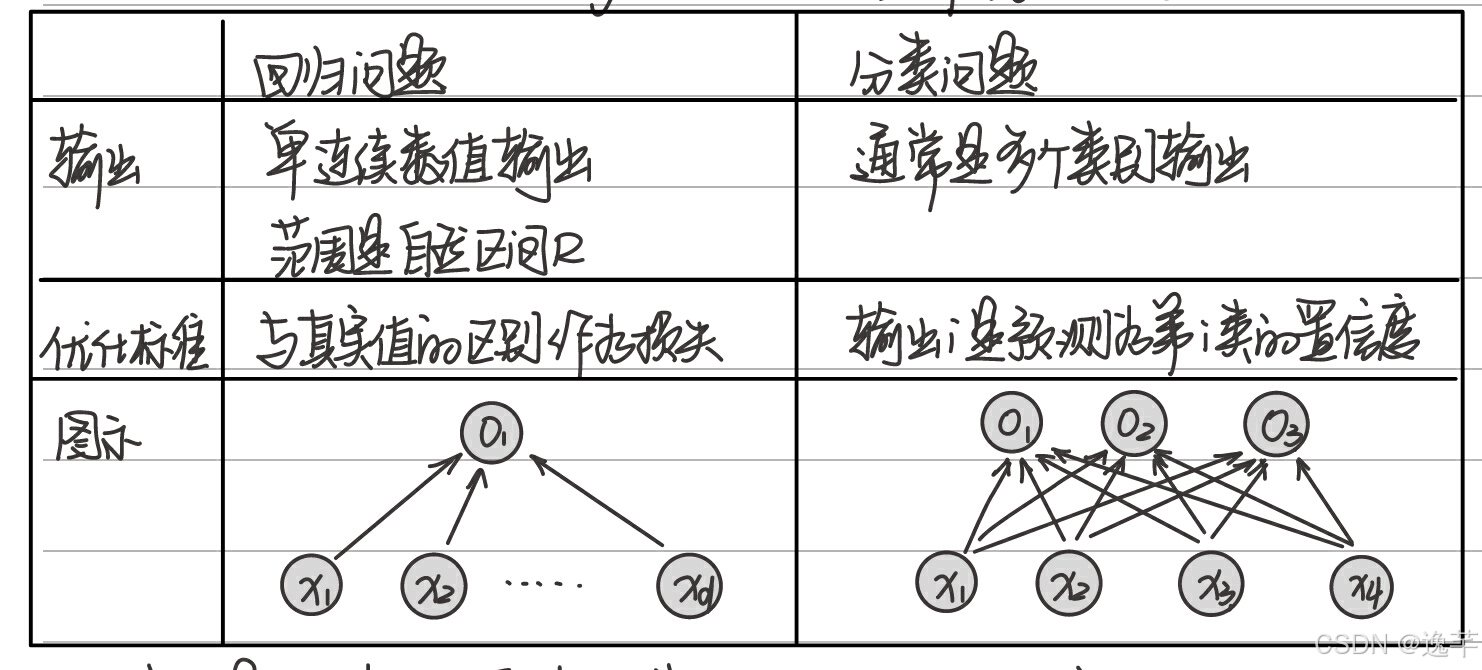
1、输出不同：分类（Classification）问题预测一个离散类别，通常是多个类别输出；回归（Regression）问题估计一个连续值，是单连续数值输出。

2、目的不同：分类的目的是寻找决策边界，用于对数据集中的数据进行分类。回归的目的是通过回归算法得到一个最优拟合线，这个线可以最好的接近数据集中的各个点。

3、结果不同：分类的结果很明确，分类正确即为对，分类错误即为错，没有逼近，最终结果只有一个。回归是对真实值的一种逼近预测，当预测值与真实值相近时，误差较小时，认为这是一个好的回归。

二、分类和回归常用的激活函数

1、为什么要使用激活函数

不使用激活函数时，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。使用激活函数能够给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，使深层神经网络表达能力更加强大。

2、激活函数分类

激活函数可以分为饱和激活函数和非饱和激活函数。

什么是饱和激活函数？假设存在激活函数f(x)

$\lim_{x\rightarrow+\infty}f{}'(x)=0$	x趋近于正无穷时，f(x)的导数趋近于0	右饱和
$\lim_{x\rightarrow-\infty}f{}'(x)=0$	x趋近于负无穷时，f(x)的导数趋近于0	左饱和
$\lim_{x\rightarrow\infty}f{}'(x)=0$	x趋近于无穷时，f(x)的导数趋近于0	饱和

不符合上述条件的即为非饱和激活函数

饱和激活函数有：sigmoid……

非饱和激活函数有：ReLU、Leaky Relu……

3、输出层常见的激活函数

对于分类问题

分类问题

目的

常用的激活函数

二分类问题

只用把目标分为两个类别，获得其分类概率值，设置分类阈值即可得到分类类别

阶跃函数、sigmoid函数

多分类问题

需要把目标分为多个类别，所得到的概率是一个向量，数值最大的数作为分类类别

softmax函数

①阶跃函数

例如对房价进行分类，要求为房价高于100万为高档住宅，低于100万为普通住宅。首先对房价进行预测，这是一个回归问题，然后设置一个单位阶跃函数，实现住宅的分类。这类问题属于二分类问题，分类结果为0,1，由此可以写出下面的公式。

阶跃函数形式简单，计算简便，但函数不光滑，不连续，对于z值无限接近于0的数据很难进行正确分类。使用很少。

②sigmoid函数（也称对数几率函数）

Sigmoid函数

对

数

几

率

函

数

优点：①将输入的正无穷大到负无穷大的连续输入变化为[0,1]的输出。

②当输入比较小时神经元被抑制，超过阈值时产生兴奋。

③输出可直接看做概率。

缺点：①输出在[0,1]，会导致多层神经网络中后面一层神经元的输入发生偏移，导致梯度下降收敛速度变慢。

②函数中含有对数运算，误差反向传播计算导数时所需时间比较长。

③导函数的范围在[0,0.25]，误差反向传播计算导数时会存在多个[0,0.25]的数相乘，导致误差经过每一层都不断衰减。如果层数较深，梯度值趋近于0，参数更新几乎停滞。

③softmax函数

使用exp（z）使输出值之间的差距拉大，大的更大，小的更小，能更好区分各个类别，最后中心化使其分布在[0,1]之间，各个概率之和为1。Softmax函数是sigmoid函数在多分类问题上的推广。

对于回归问题

输出层一般使用线性激活函数，使模型的输出值可以覆盖整个实数域。

4、隐藏层常见的激活函数

ReLU函数
ReLU函数	Leaky-ReLU函数	PReLU函数和 RReLU函数
优点：①z>0时，导数等于1，缓解了梯度消失问题。 ②不存在幂运算，计算速度快。 ③导数恒等于1，训练模型收敛速度快。	优点：①避免了ReLU神经元死亡 ②神经网络的计算和训练速度快	PReLU函数：参数化修正线性单元，a是可训练参数； RReLU函数：训练阶段，负值部分的斜率是随机分配的（均匀分布）；测试阶段，负值的斜率是固定的（训练阶段所有α的平均值）
缺点：①输出不是以0为均值的，会影响收敛的速度 ②z<0时，梯度为0，神经元死亡	缺点：超参数a需要人工调整
		PReLU函数：

双

曲

正

切

函

数

优点：①将输入的正无穷大到负无穷大的连续输入变化为[-1,1]的输出，避免了Logistic函数存在的输入偏移问题。

缺点：①函数中含有对数运算，误差反向传播计算导数时所需时间比较长。②导函数的范围在[0,1]同样存在梯度消失问题。

三、分类和回归常用的损失函数

1、为什么要使用损失函数

在模型训练的过程中，损失函数用于计算模型预测的输出与实际标签之间的差异。这个差异值，即损失值，能够直观地反映出模型在当前参数下的性能。通过最小化这个损失值，我们可以驱使模型不断学习和改进，直至达到满意的预测精度。

2、常见的损失函数

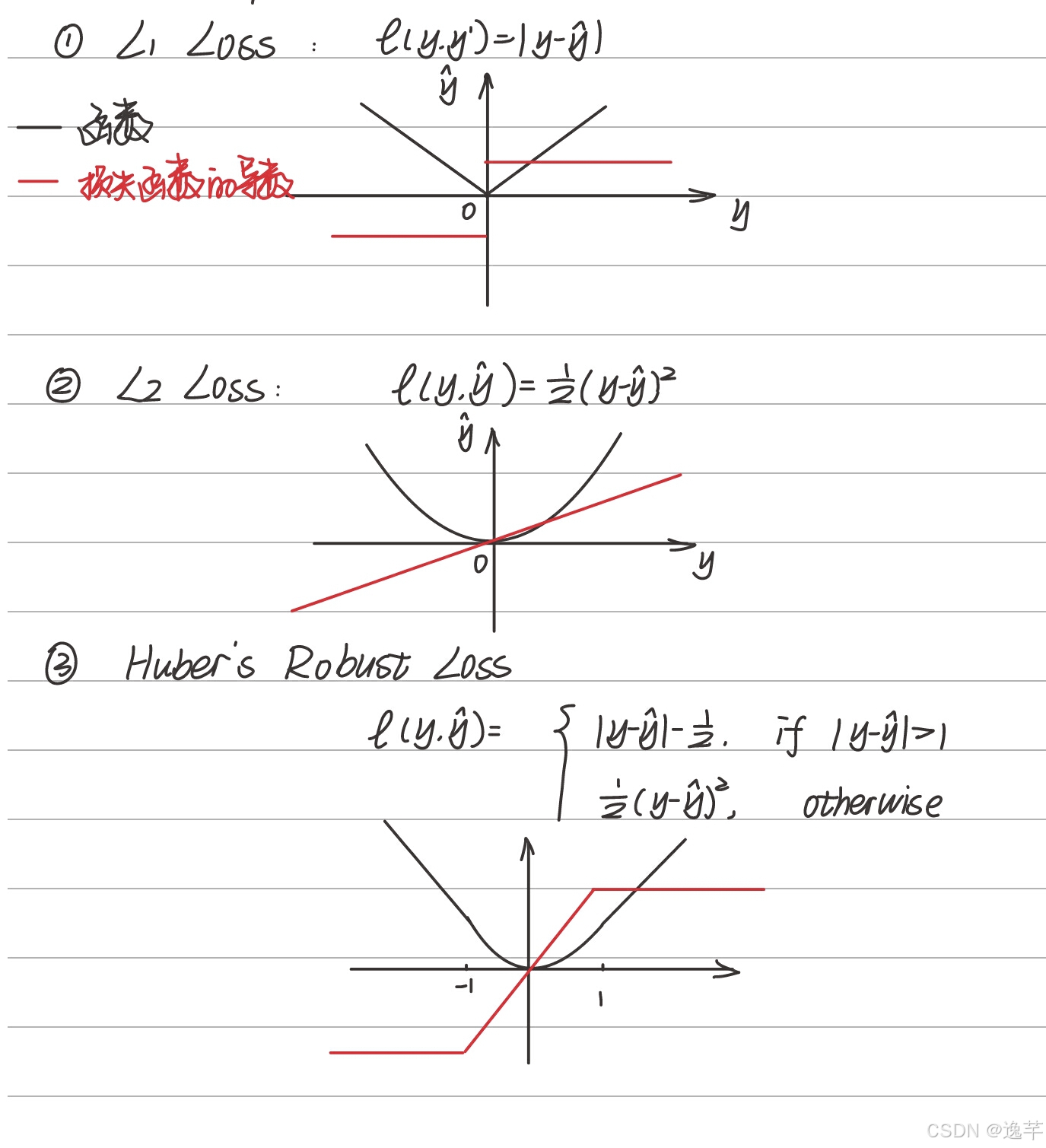
基于距离度量的损失函数

L1 Loss、L2 Loss、Huber's Robust Loss

基于概率分布度量的损失函数

交叉熵损失函数：用于衡量模型输出的概率分布与真实概率分布之间的差异。常用于分类问题中。

二分类问题	交叉熵损失函数
	平均交叉熵损失函数
	平均交叉熵损失函数求导数
多分类问题	多分类交叉熵损失函数

为什么分类问题中常使用交叉熵损失函数而没有使用均方差函数呢？

如下图证明所示，使用梯度下降法更新w和b时，sigmoid函数求导数会存在很多趋于0的数，使得迭代更新时更新缓慢。而使用交叉熵损失函数不需要对sigmoid函数求导数。

四、常见的分类和回归算法

1、回归算法：主要用于预测数值型数据。

线性回归（Linear Regression）：这是最基本和常见的回归算法，它假设因变量和自变量之间存在线性关系，并通过最小化预测值和实际值之间的平方差来拟合数据。
线性回归实现见前一篇文章深度学习实现——线性回归-CSDN博客
决策树回归（Decision Tree Regression）：决策树回归是一种基于树结构的回归方法，它通过构建决策树来划分数据空间，并在每个叶节点上拟合一个简单的模型（如常数或线性模型）。
随机森林回归（Random Forest Regression）：随机森林回归是一种集成学习方法，它通过构建多个决策树并将它们的预测结果组合起来来提高回归性能。能够处理高维数据和非线性关系。

2、分类算法：主要用于发现类别规则并预测新数据的类别。

逻辑回归（Logistic Regression）：尽管名字中有“回归”，但实际上逻辑回归是一种分类算法，常用于二分类问题。它通过逻辑函数将线性回归的输出映射到(0,1)之间，得到样本点属于某一类别的概率。
支持向量机（SVM）：支持向量机是一种基于统计学习理论的分类算法。它通过寻找一个超平面来最大化不同类别之间的间隔，从而实现分类。SVM在高维空间和有限样本情况下表现出色，并且对于非线性问题也可以使用核函数进行扩展。
K近邻（KNN）：K最近邻是一种基于实例的学习算法，它根据输入样本的K个最近邻样本的类别来确定输入样本的类别。