MATLAB-非线性规划

於是很爱我

已于 2024-04-17 09:16:15 修改

阅读量736

点赞数 19

文章标签： matlab 算法人工智能

于 2024-04-16 21:58:27 首次发布

本文链接：https://blog.csdn.net/2301_79759888/article/details/137795693

版权

本文介绍了非线性规划模型的基本概念，包括数学形式、线性与非线性方程的区别，以及全局最优解和局部最优解的定义。着重讨论了无约束和有约束规划问题的求解策略，以平板电视生产利润函数为例，展示了梯度下降算法在实际问题中的应用。最后给出了梯度下降算法的理论基础和具体实例，包括二维和一维函数的极值求解。

摘要由CSDN通过智能技术生成

1. 非线性规划模型

非线性规划的数学形式（1）

非线性规划的数学形式（2）：采用向量表示

非线性规划的数学形式（3）：将线性约束与非线性约束分离

例题：求函数在区间[a,b]且在x0附近的极值（二维函数求极值）

例题：求函数在区间[a,b]且在x0附近的极值（一维函数求极值）

1. 非线性规划模型

非线性规划的数学形式（1）

其中， $z = f(\vec{x}), g_{i}(\vec{x})\leqslant 0$ 或者是 $h_{j}(\vec{x})= 0$ 中至少有一个为非线性方程，则称该模型为非线性规划模型

非线性规划的数学形式（2）：采用向量表示

非线性规划的数学形式（3）：将线性约束与非线性约束分离

关于线性方程和非线性方程

在线性代数中，线性方程和非线性方程是描述数学关系的两种不同类型的方程。

1. 线性方程：
- 线性方程是指其未知数的最高次数为一次的方程。例如，形如 ax + b = 0 的一元线性方程，或形如 ax + by = c 的二元线性方程。
- 线性方程的特点是未知数的次数都是一次，且各个未知数之间没有乘积项或其他非线性项。

2. 非线性方程：
- 非线性方程是指其未知数的最高次数不为一次的方程。这意味着方程中可能包含平方项、立方项、乘积项或其他非线性项。
- 例如，x^2 + y^2 = r^2 是一个二元的非线性方程，e^x - 2y = 0 是一个一元的非线性方程。

3. 区别：
- 主要区别在于方程中未知数的次数。线性方程中未知数的次数都是一次，而非线性方程中未知数的次数可以是二次、三次或更高次。
- 线性方程的图像通常是直线（或平面），而非线性方程的图像则可能是曲线、曲面或其他形状。
- 求解线性方程通常更为直接，可以使用代数方法解析求解，例如消元法、逆矩阵法等。而非线性方程的求解通常更为复杂，可能需要数值方法或近似求解。

2. 非线性规划模型的概念和理论

对于如下模型：

非线性规划问题的可行域

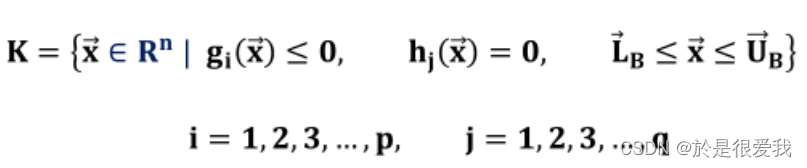
全局最优解和局部最优解

若 $\vec{x} \epsilon K$ ，且 $\forall \vec{x} \epsilon K$ ，都有 $f(\vec{x*}) \leqslant f(\vec{x})$ ，则称 $\vec{x*}$ 为该规划问题全局最优解， $f(\vec{x*})$ 为全局最优值。
若 $\vec{x*} \epsilon K$ ，且存在的邻域 $N_{\delta }(\vec{x*})$ ，且 $\forall \vec{x} \epsilon N_{\delta }\cap K$ ，有 $f(\vec{x*}) \leqslant f(\vec{x})$ ，则称 $\vec{x*}$ 为该规划问题的局部最优解， $f(\vec{x*})$ 为局部最优值

无约束规划问题的求解

无约束规划的数学形式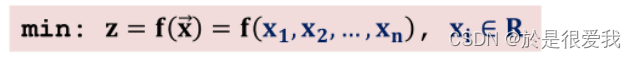

定理：无约束规划问题局部最优解的充分条件：设 $f(\vec{x})$ 具有连续二阶偏导数，且 $\vec{x*}$ 满足 $\triangledown f(\vec{x*}) = 0$ 并且 $\triangledown ^{2}f(\vec{x})$ 为正定矩阵，则 $\vec{x*}$ 是无约束问题的局部极小点

$\triangledown f(\vec{x})$ 表示函数的 $f(\vec{x})$ 的梯度（一阶偏导数向量）。
$\triangledown ^{2}f(\vec{x})$ 表示函数的 $f(\vec{x})$ 的二阶偏导数。

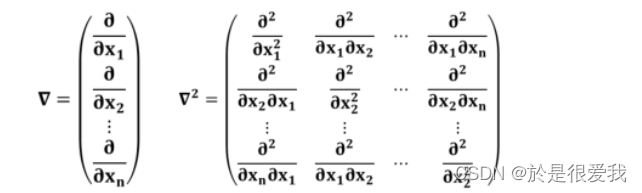
有约束规划问题的求解

有约束规划问题的求解的一般思路

3. 非线性规划问题

问题描述

问题分析与模型建立

设两种型号平板电视的产量为决策变量，列出利润函数，求利润函数的最值

列式求出利润函数的值

模型建立

f(x1,x2)作为求最大值的目标函数，x1、x2作为决策变量，可以将问题转换为在区域 $S = \left \{ \left ( x1,x2 \right ) \mid x1 \geqslant 0,x2\geqslant 0 \right \}$ 内求函数f(x1,x2)的最值

$f(x1,x2) = -0.01* x1^{2} - 0.007 * x1 * x2 -0.01 *x2^{2} + 144 * x1 + 174 * x2 - 4000$

根据函数进行绘图

在这段代码中，通过以下语句设置了变量的取值范围和步长：
x1 = 0:100:10000;
x2 = 0:100:10000;

这里使用了 MATLAB 中的冒号操作符来定义向量。冒号操作符的一般形式是 `start:step:end`，其中 `start` 是起始值，`step` 是步长，`end` 是结束值。在这个例子中，`x1` 和 `x2` 都从0开始，步长为100，直到10000结束。这意味着 `x1` 和 `x2` 的取值范围是从0到10000，且每次递增100。

clc,clear,format long g % 设置显示格式为 long g，以便显示更多小数位
% 设置变量的取值范围和步长
x1 = 0:100:10000;
x2 = 0:100:10000;
% 生成 x1 和 x2 的网格
[x1,x2] = meshgrid(x1,x2);
% 计算利润函数
c = 400000 + 195 * x1 + 225 * x2;
p1 = 339 - 0.01 * x1 - 0.003 * x2;
p2 = 399 - 0.004 * x1 - 0.01 * x2;
f = p1 .* x1 + p2 .* x2 - c;
% 绘制利润函数的三维网格图
figure(1)
mesh(x1,x2,f);
% 设置 xy 轴标签，使用 LaTeX 解释器
xlabel('$x_1$','Interpreter','Latex')
ylabel('$x_2$','Interpreter','Latex')
zlabel('profit')
figure(2)
contour(x1,x2,f,20,'color','b','ShowText','on');% 20 条等高线，蓝色显示，并显示数字标签
xlabel('$x_1$','Interpreter','Latex')
ylabel('$x_2$','Interpreter','Latex')

理论求解（求导）

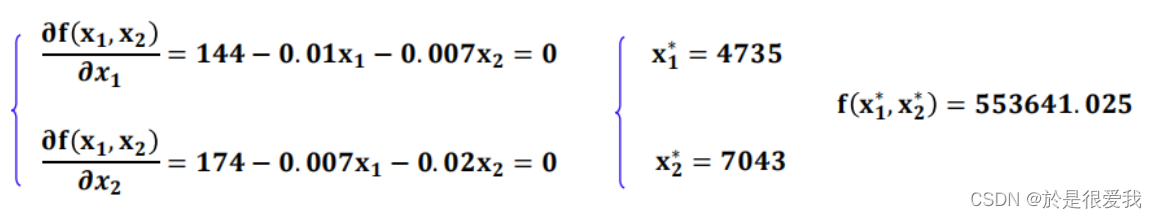
这家公司可以通过生产4735台19英寸彩电和7043台21英寸彩电来获得大利润，每年获得的净利润为553641.025美元。
每台19英寸彩电的平均售价为270.52元，每台21英寸彩电的平均售价为309.63元。生产的总支出为2908000元，相应的利润率为19%。

梯度下降算法

1. 基本理论

梯度下降算法是无监督机器学习中的常用算法，通过不断迭代计算函数的梯度，判断该点的某一方向和目标之间的距离，最终求得最小的损失函数

梯度下降算法学习

ppt写的很杂，可以看我前面的链接视频比较好理解一些。我在这里只做简单的总结

梯度算法是一种常用的优化算法，用于求解函数的最小值或最大值。它基于函数的梯度（或者梯度的反方向）指示了函数增长最快的方向。梯度算法的基本思想是沿着梯度的反方向（或者梯度的负方向）迭代地调整参数，以期望能够逐步接近函数的最小值点。

梯度算法的基本步骤：

定义代价函数
选择起始点
计算梯度
按学习率前进
重复3、4步直到找到最低点

2. 梯度下降算法举例

例题：求函数在区间[a,b]且在x0附近的极值（二维函数求极值）

求函数f(x1,x2) = (x1 - 1.0012) + (x2 - 1.9321) + 2.331 在实数域内的极值

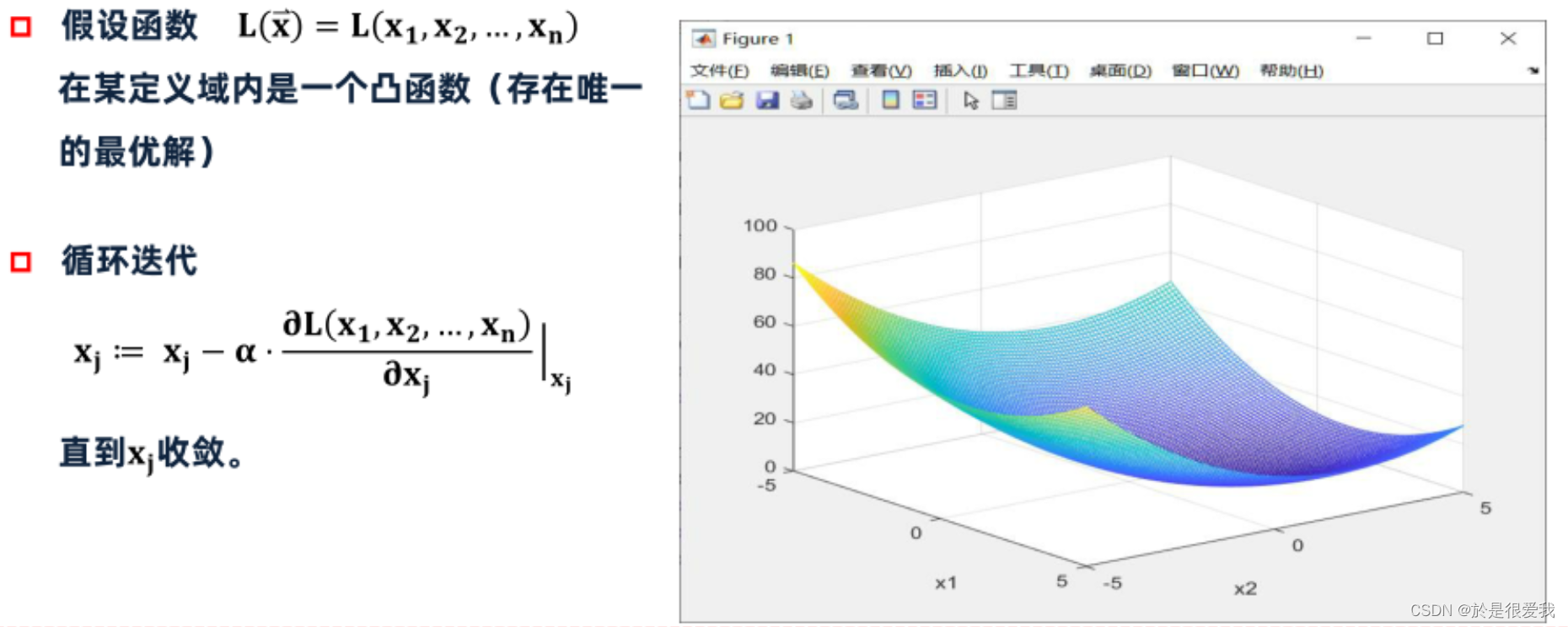
先绘制一下均方误差的最小化损失函数的图像：

clc;clear;
% 定义 x1 和 x2 的取值范围和步长
x1 = -5:0.1:5;
x2 = -5:0.1:5;
% 生成 x1 和 x2 的网格
[x1,x2] = meshgrid(x1,x2);
% 计算函数值
y = LossFun(x1,x2);
% 创建新图形窗口
fig1 = figure(1);
% 绘制函数的三维网格图
s = mesh(x1,x2,y);
xlabel('x1');
ylabel('x2');

% 定义函数 LossFun，用于计算函数值
function y = LossFun(x1,x2)
y = (x1 - 1.0012).^2 + (x2 - 1.9321).^2 + 2.331;
end

定义所需函数：

% 定义主函数
% 初始点的x1和x2值('x10'和'x20')、学习率'alpha'、停止条件'tol'和最大迭代次数'maxIter'
% 函数返回最小值点'x1min' 和 'x2min'，以及函数的最小值'fmin'和路径'Path'
function [x1min,x2min,fmin,Path] = gradientDescent(x10,x20,alpha,tol,maxIter)

% 设置初始点
x1 = x10; x2 = x20; 

% 初始化路径矩阵 Path，将初始点和对应的函数值存储在其中。
Path(1,1) = x1; Path(2,1) = x2;
Path(3,1) = LossFun(x1,x2);


for iter = 1:maxIter % 迭代过程，迭代次数不超过最大迭代次数
    % 计算当前点梯度值
    grandValueX1 = GradFunX1(x1);
    grandValueX2 = GradFunX2(x2);
    % 根据梯度和学习率更新当前点的值
    x1 = x1 - alpha * grandValueX1; 
    x2 = x2 - alpha * grandValueX2;
    % 将更新后的点和对应的函数值添加到路径矩阵 Path 中。
    Path = [Path,[x1;x2;LossFun(x1,x2)]];
    % 检查梯度的范数是否小于设定的停止条件 tol，如果是，则跳出迭代循环。
    if sqrt(abs(grandValueX1) + abs(grandValueX2)) < tol
        break;
    end
end
% 计算最终函数值
fmin = LossFun(x1,x2);
% 返回最小值点和函数值
x1min = x1; x2min = x2;
end

% 定义了目标函数 LossFun(x1, x2)，即要最小化的函数。
function y = LossFun(x1,x2)
y = (x1 - 1.0012).^2 + (x2 - 1.9321).^2 + 2.331;
end

% 定义了分别关于变量 x1 和 x2 的梯度函数。
function g = GradFunX1(x1)
g = 2.*(x1-1.0012);
end

function g = GradFunX2(x2)
g = 2.*(x2-1.9321);
end

使用梯度算法求解

clc;clear;
x10 = -5; x20 = -5; % 初始点
alpha = 0.2;% 学习率（步长）
tol = 1e-6; % 收敛阈值
maxIter = 100000; %最大迭代次数

% 执行梯度下降
[x1min,x2min,fmin,Path] = gradientDescent(x10,x20,alpha,tol,maxIter);

% 绘制下降搜索路径
s = plot(Path(1,:),Path(2,:),'LineWidth',3);
x1min,x2min % 显示极值点

例题：求函数在区间[a,b]且在x0附近的极值（一维函数求极值）

求函数f(t) = [cos(0.1 * t) - 1]( t - 2 ) 在区间[0, 200]的极值

函数图像：

clc;clear all;
% 定义函数
textFun = @(t)(cos(0.1*t)-1).*(t-2);
% 生成t向量，范围为0-200，共500个点
t = linspace(0,200,500);
% 计算函数在时间t上的取值
y = textFun(t);
% 绘制图像
plot(t,y,'Color','r','LineWidth',2);
xlabel('t')
ylabel('f(t)')
grid on % 打开网格线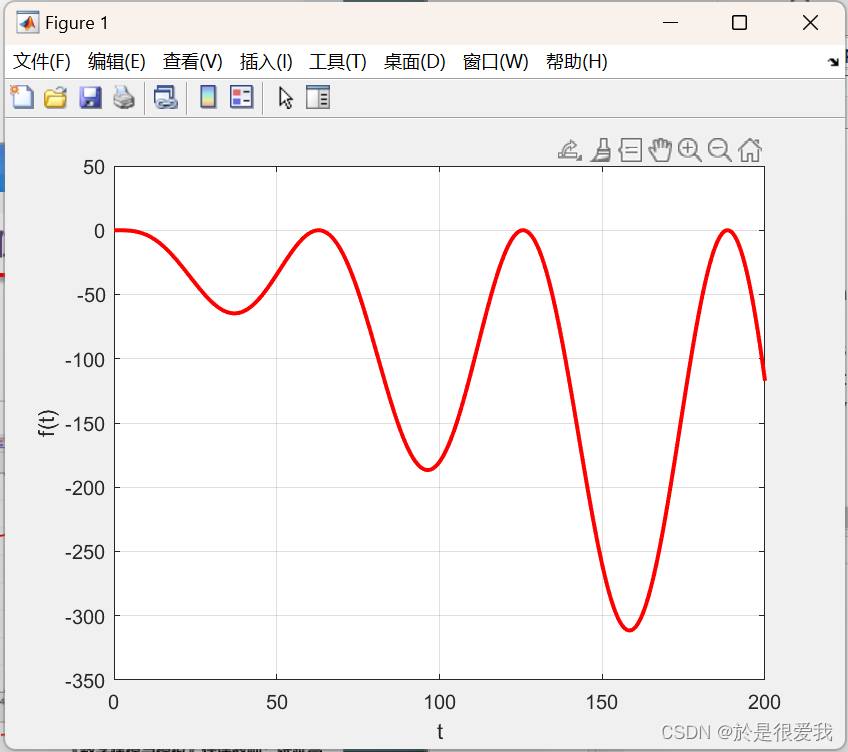

clc;clear all;
% 定义函数
textFun = @(t)(cos(0.1*t)-1).*(t-2);
t0 = 100;% 初始点
alpha = 0.01;% 学习率
MaxIter = 1000; % 最大迭代次数
tol = 1e-6;% 容差

t = t0;
for iter = 1 : MaxIter
    gradient = GradDistance(t);
    newt = t - alpha * gradient;
    if abs(newt - t) < tol
        break;
    end
    t = newt;
end

fprintf('极值点: t = %.4f\n', t);
fprintf('极值: %.4f\n', textFun(t));

% 定义梯度函数
function grad = GradDistance(t)
grad = -0.1 * sin(0.1 * t) * (t - 2) + (cos(0.1 * t) - 1);
end