Python 可视化地图投影变形，看懂“地球被压平如何变形”

刚出生被寄予厚望

已于 2025-10-01 09:50:09 修改

阅读量744

点赞数 27

CC 4.0 BY-SA版权

分类专栏：软件代码分享文章标签： python

于 2025-10-01 09:26:52 首次发布

本文链接：https://blog.csdn.net/2301_79953895/article/details/152334982

软件代码分享专栏收录该内容

9 篇文章

订阅专栏

基本介绍

关键词：地图投影，投影变形，可视化，墨卡托投影，方格投影，桑逊投影，摩尔威德投影，附源码和可执行文件
这个工具用于帮助理解地图投影中的变形特性。
你可以在地图上任意设置一个位置和大小的圆形，观察它在不同投影下的形状变化。
提供了墨卡托投影、方格投影、桑逊投影等多种常见的投影方式。
实际上，这是一个很简单的软件，实际用处可能没有很大。但可以把这个当做单纯用来玩的小项目，或者在地图学课堂上用来教学展示，对地图投影比较感兴趣的朋友可以试一下。
本文项目源代码链接：https://gitee.com/Orange_867/map-projection-drawing（欢迎访问我的 Gitee 仓库，来看一下吧🙏😊）
可执行文件下载链接：https://pan.baidu.com/s/1poAogtKXlBJN7fLYmbdDEQ?pwd=5452

初始界面

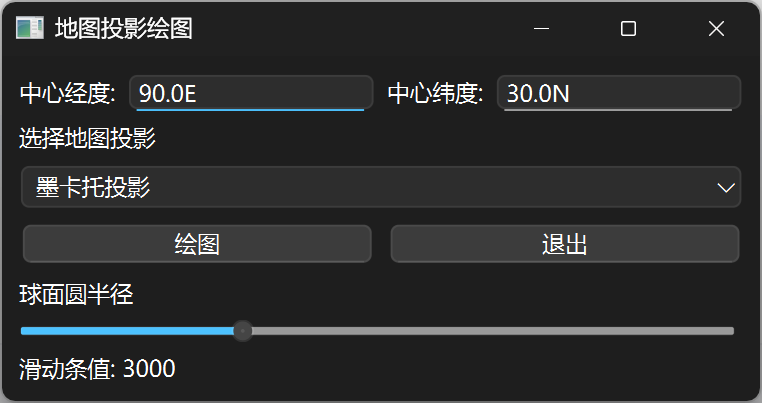
在这里插入图片描述

操作说明

从下拉菜单中选择一种地图投影方式
设置中心经度和中心纬度 —— 这将是图中变形椭圆的中心位置
拖动滑条，调整球面圆形的半径大小
绘制出来的图形如下：

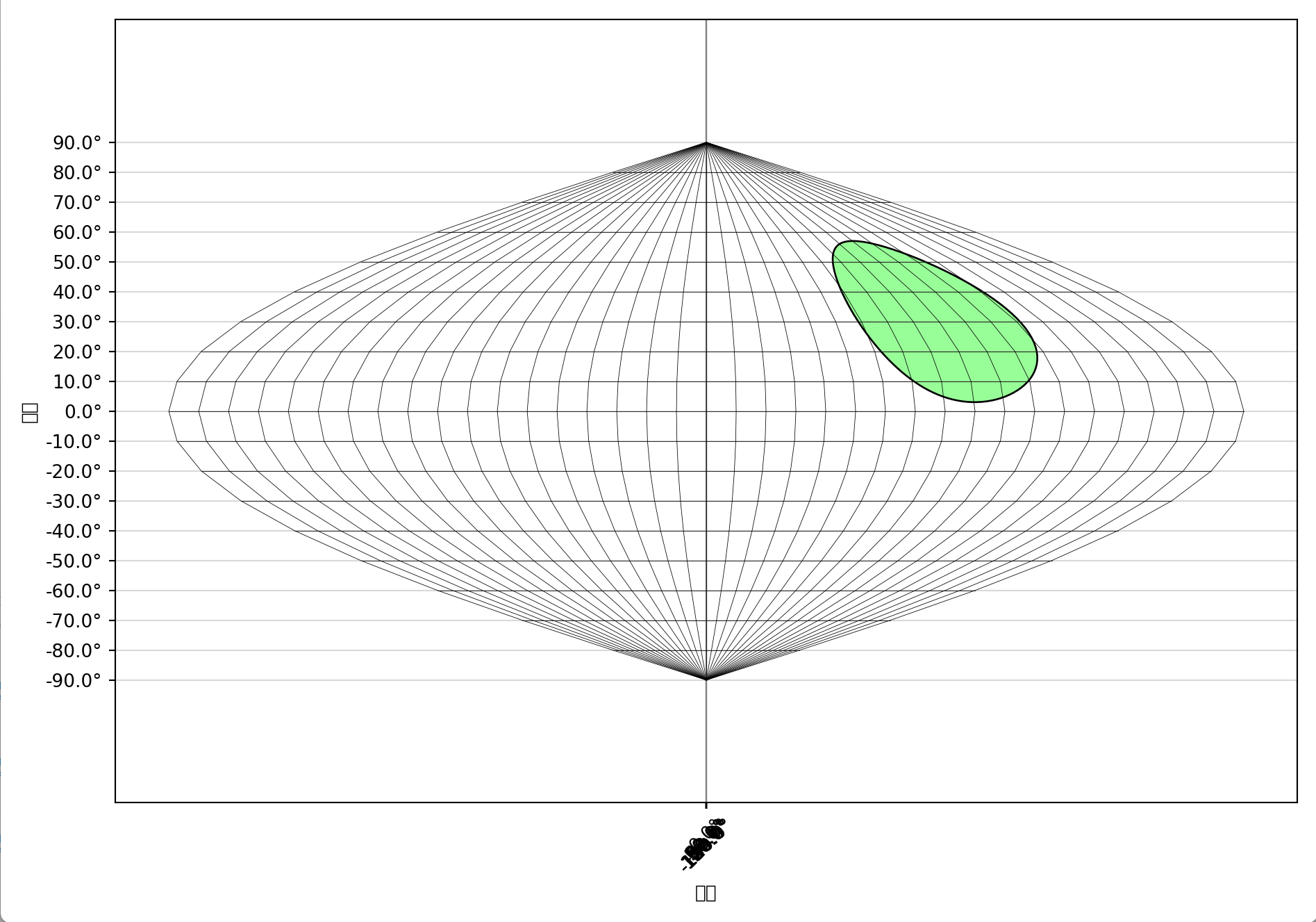
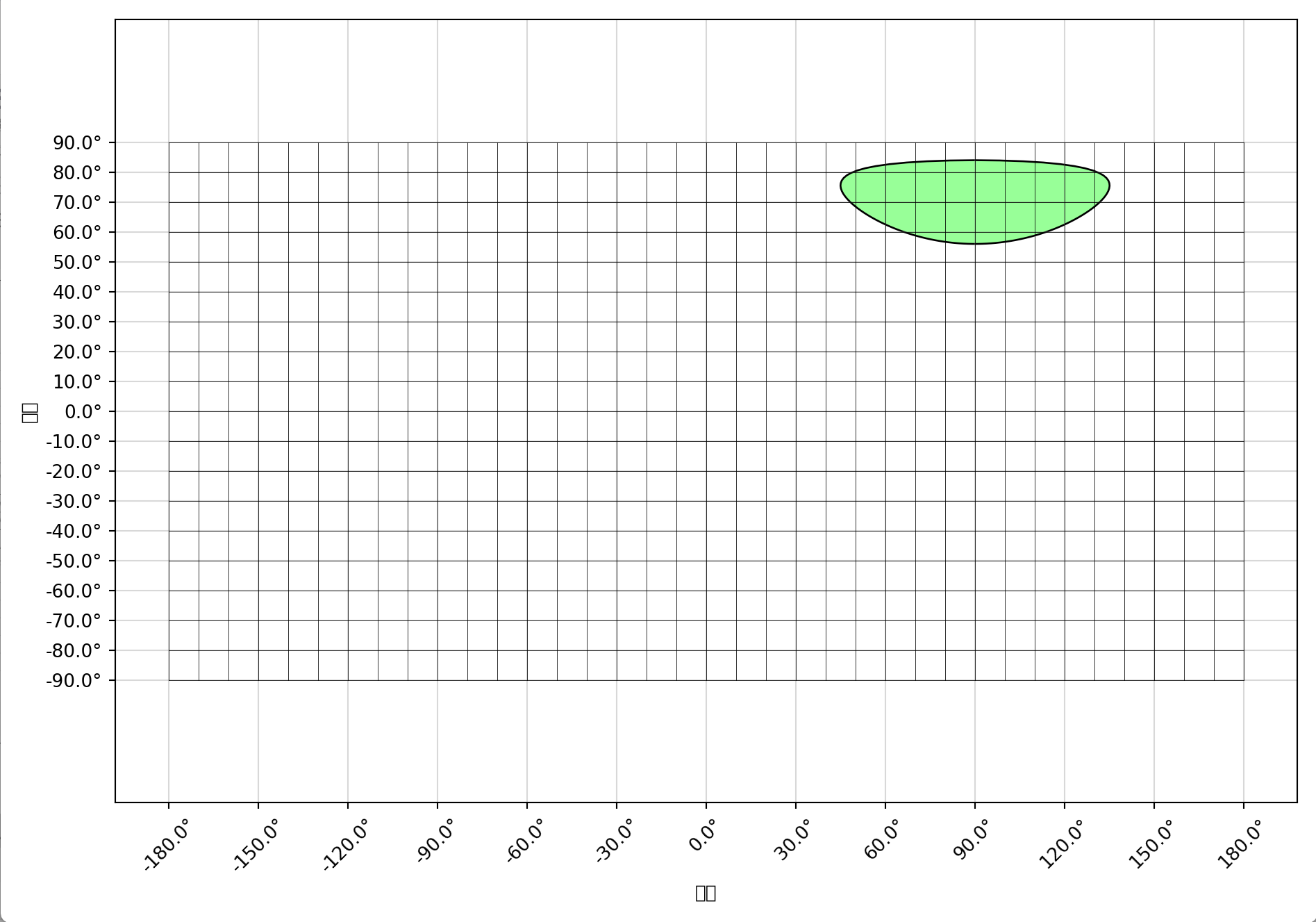
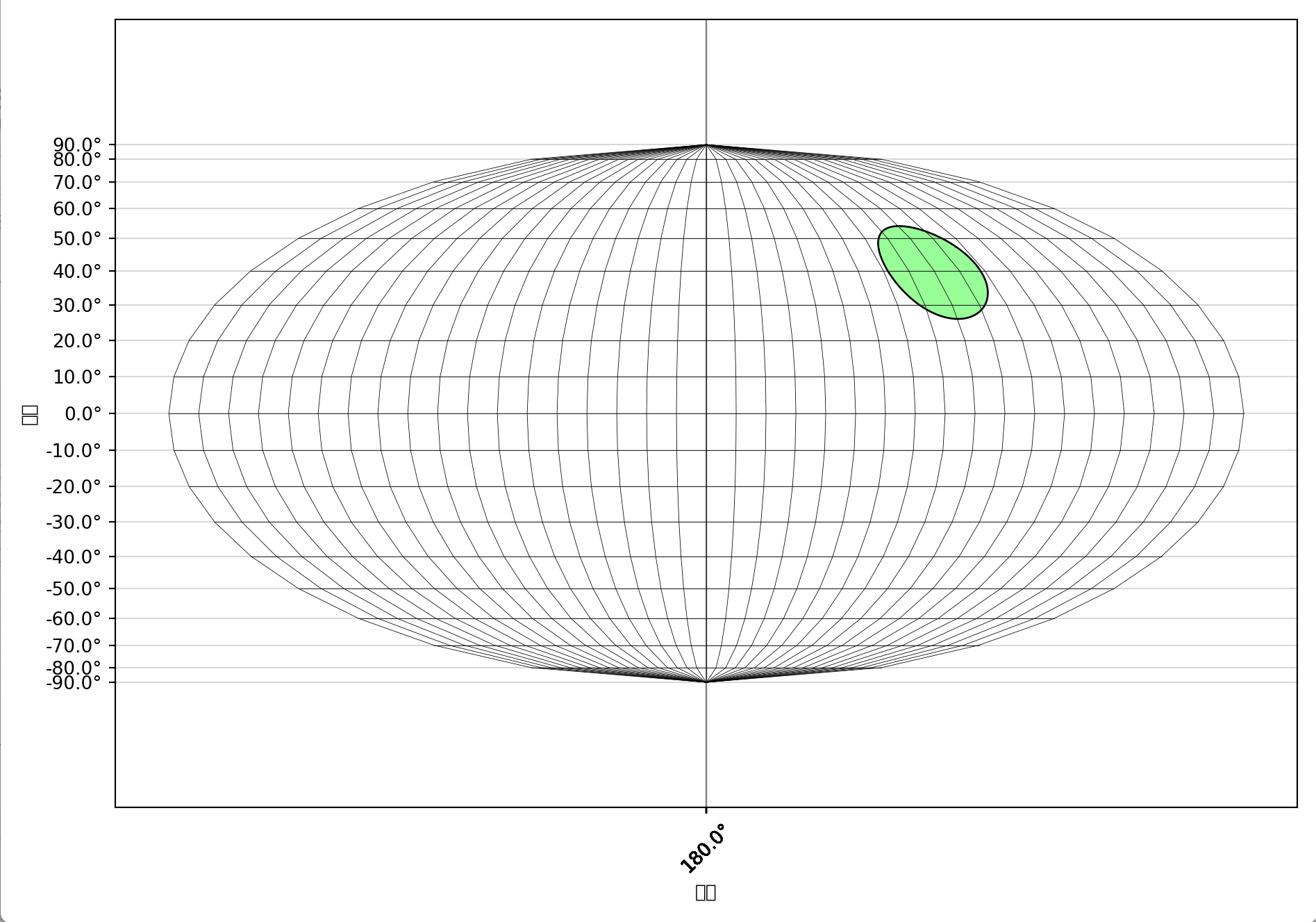
特别地：
当圆形的半径设得非常小（例如约100km）时，它就相当于一个微分圆。
此时，该圆在投影后的形状近似为一个椭圆，称为变形椭圆，能直观反映该点处的拉伸或压缩情况。

放大查看该区域，你会发现投影后的图形与椭圆非常接近：
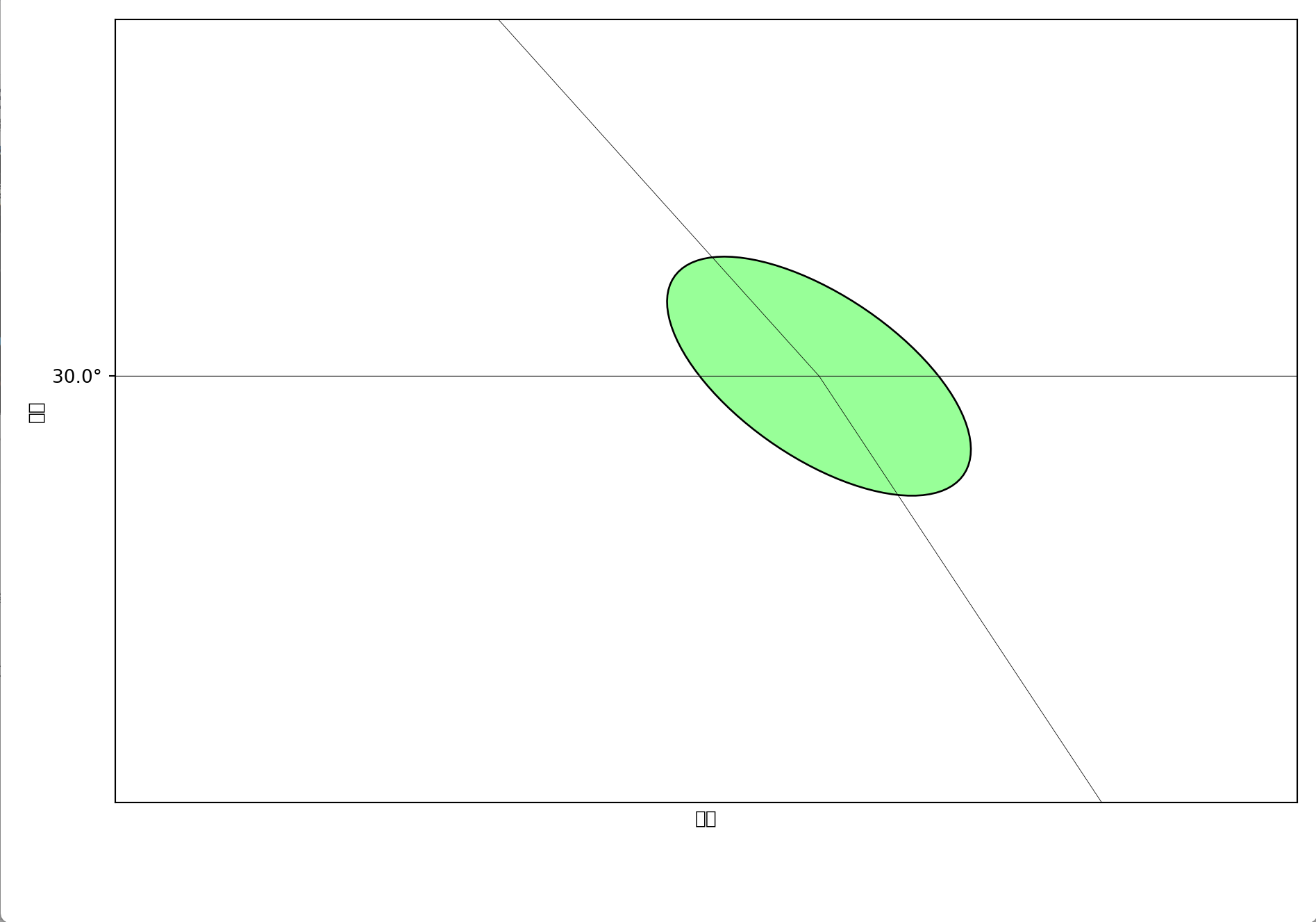
在这里插入图片描述

值得注意的是

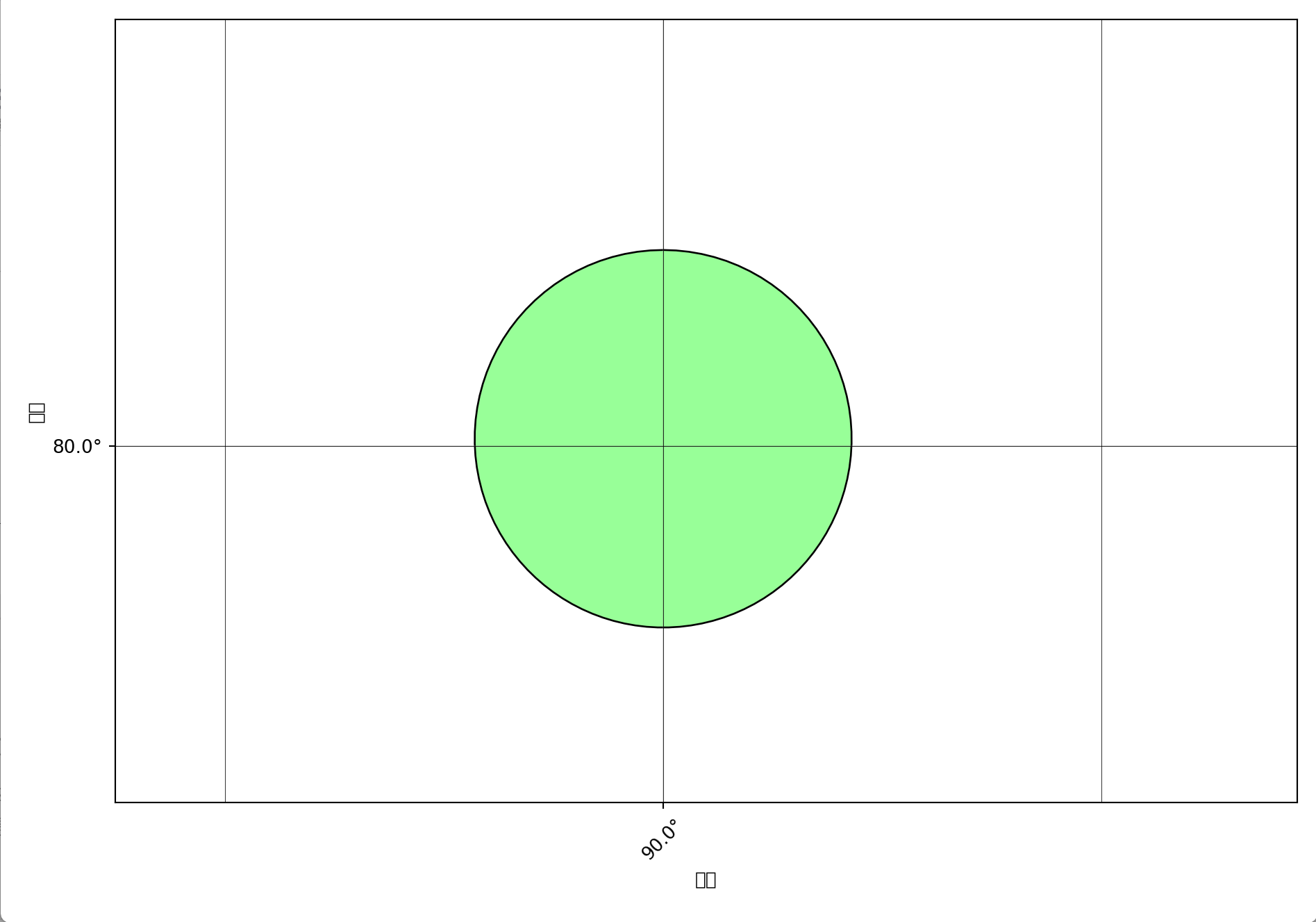
墨卡托投影作为等角投影的一种，虽然在高纬度地区的面积变形非常严重，但是微分椭圆经过投影依然是一个完美的圆，不论在什么位置。

包含的地图投影类型

1. 墨卡托投影（Mercator Projection）

等角圆柱投影，保持方向和角度不变，非常适合航海导航使用。但该投影在高纬度地区会产生明显的面积变形，例如格陵兰岛在地图上看起来比实际大得多。

2. 方格投影（Square Grid Projection）

这是一种简化的投影方式，将经纬度直接映射为平面坐标。虽然会产生严重的形状和面积变形，但因其简单性常用于教学演示。

3. 正轴等积圆柱投影（Cylindrical Equal-Area Projection）

这种投影方式保持了面积的准确性，纬线间距随纬度增加而压缩。非常适合用于展示全球面积分布，但在高纬度地区形状会有明显拉伸。

4. 桑逊投影（Sanson Projection）

也称为桑逊-佛兰斯泰德投影，是一种等积伪圆柱投影。赤道和中央经线为直线，其他经线呈正弦曲线形状。常用于世界地图绘制，在两极区域会有一定的水平拉伸。

5. 水母投影（Jellyfish Projection）

水母投影和桑逊在数学上非常相似，但通常正弦投影中央经线是直的，其他经线是正弦曲线。

6. 蝴蝶投影（Butterfly Projection）

形似蝴蝶翅膀。这里是一种变体，仅仅是比较好看，实际上并没有什么实际用处。

7. 摩尔威德投影（Mollweide Projection）

等积伪圆柱投影，整个地球呈现椭圆形（宽高比为2:1）。非常适合展示全球分布数据，如气候图、人口图等。虽然边缘区域会有一定形状扭曲，但能保证面积的准确性。

代码原理介绍

当用户点击绘图按钮后，程序开始执行地图投影的绘图。

首先，读取当前界面中的参数设置，包括球面圆形的中心位置（经纬度）、半径大小，以及所选的地图投影类型。

接着，程序生成两类关键点集：

经纬度网格点集：在经纬度范围内，按固定间隔均匀采样经纬度坐标，构成用于绘制经纬网的离散点集；
球面圆形点集：根据设定的中心与半径（在地球球面取小圆，半径其实不可能超过6371 km），在地球球面上计算出圆周上均匀分布的100个点的经纬度坐标，用于模拟一个球面圆（很小时可视为微分圆）。

随后，这两个点集被分别传入对应投影类型的计算函数（如墨卡托、桑逊等）。投影函数依据各自的数学规则，将每个点的经纬度（b, l）转换为平面直角坐标（x, y），并返回包含原始经纬度和平面坐标的新的点对象列表。

绘图阶段分为两部分：

经纬网格绘制：将所有具有相同纬度的点按经度顺序连接，形成纬线；将所有具有相同经度的点按纬度顺序连接，形成经线。虽然连接逻辑基于经纬度的一致性，但实际绘制时使用的是投影后的平面坐标（x, y），从而呈现出不同投影下特有的网格形态。
球面圆形绘制：将投影后的圆形边界点依次连接，并闭合形成封闭图形，同时进行颜色填充，以直观展示该区域在特定投影下的形变特征（即“变形椭圆”）。

通过这一流程，可以清晰观察到不同投影方式对形状、面积和角度的影响。

项目结构介绍

.
├── Form.py          # GUI界面定义，和主要的操作
├── Point.py         # 点坐标类定义
├── Plotter.py       # 绘图功能实现
├── Projection.py    # 投影类（计算规则）实现
└─── main.py          # 程序入口

main.py非常简短，仅仅是把窗体运行起来
Form.py这个其实才是最主要的文件，大多数的代码都在其中
包括窗体搭建
生成球面圆形一周的点的经纬度坐标
生成经纬度网格点的坐标
统一调度其他函数实现功能

Plotter.py将投影后的球面圆形和经纬网格一种展绘出来

Projection.py结构比较简单，但是方便拓展，容易增加新的投影方式

如何添加新的地图投影方式

本项目结构清晰，支持快速扩展新的投影类型。可以自己编写新的投影方式。

第一步：在界面下拉菜单中添加选项

打开 Form.py 文件，找到创建下拉框的代码部分，在 addItems 列表中加入你想要新增的投影名称。例如：

self.combo_box = QComboBox()
self.combo_box.addItems([
    "墨卡托投影", 
    "方格投影", 
    "正轴等积圆柱投影", 
    "桑逊投影", 
    "水母投影", 
    "蝴蝶投影", 
    "摩尔威德投影"
    # 在这里添加新的投影名称，如："自定义投影"
])

第二步：为新投影编写处理逻辑

在 Form.py 的投影调用逻辑中（通常是 elif 判断块），添加对新投影名称的响应，并调用对应的投影函数。例如：

elif self.combo_box.currentText() == "摩尔威德投影":
    new_grid_points = projection.Mollweide(grid_points)
    new_circle_points = projection.Mollweide(circle_points)
# 可以添加新的判断，如：
# elif self.combo_box.currentText() == "自定义投影":
#     new_grid_points = projection.CustomProjection(grid_points)
#     new_circle_points = projection.CustomProjection(circle_points)

第三步：实现投影计算函数（在 `Projection.py` 中）

这是核心部分。你只需在 Projection.py 文件中定义一个新函数，输入是一组包含经纬度的点（Point 对象列表），输出是经过投影变换后的平面坐标点集。

函数模板如下（以墨卡托投影为例）：

def Mokatuo(self, points):
    """
    墨卡托投影：保持角度不变，适合导航
    参数:
        points: Point对象列表，每个包含纬度b、经度l
    返回:
        投影后的Point列表，包含x, y平面坐标
    """
    R = 6378137  # 地球半径（米）
    projected_points = []
    
    for point in points:
        lat_rad = math.radians(point.b)  # 纬度转弧度
        lon_rad = math.radians(point.l)  # 经度转弧度

        x = lon_rad * R
        # 限制纬度范围，防止极点发散
        safe_lat = max(-85, min(85, point.b))
        safe_lat_rad = math.radians(safe_lat)
        y = R * math.log(math.tan(math.pi/4 + safe_lat_rad/2))

        # 创建新点，保留原始经纬度，记录投影坐标
        new_point = Point(x=x, y=y, b=point.b, l=point.l)
        new_point.isprocessed = True  # 标记已处理
        projected_points.append(new_point)

    return projected_points