评估分类模型之绘制ROC曲线及PC曲线

炸炸炸炸炸芋头

已于 2025-03-30 17:10:31 修改

阅读量792

点赞数 23

文章标签：人工智能机器学习

于 2025-03-30 17:09:19 首次发布

本文链接：https://blog.csdn.net/2301_80378324/article/details/146765449

版权

1.1 精确率：预测为正例的样本中真正正例的比例

1.2 召回率：真正正例被预测为正例的比例

1.1 真正例率（TPR）：即召回率，反映了模型正确识别正例的能力

1.2 假正例率（FPR）：假正例占负例的比例，反映了模型将负例错误识别为正例的概率

一、模型评估综述

1. 什么是模型评估

模型评估是指在机器学习和其他相关领域中，对训练好的模型进行性能评估和分析的过程。其目的是衡量模型在实际应用中的表现，判断模型的优劣，以及确定模型是否能够满足特定的任务需求。

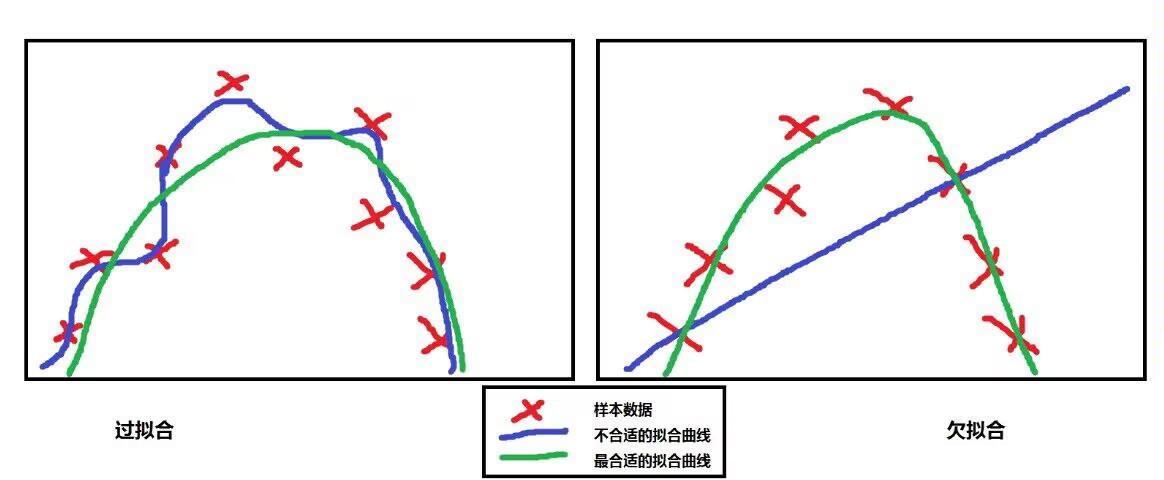
2. 过拟合、欠拟合

2.1 过拟合

定义：模型在训练数据集上表现得非常好，能够几乎完美地拟合训练数据，但是在新的、未见过的数据（测试数据集）上表现却很差，泛化能力弱。原因：模型过于复杂，学习了训练数据中的噪声和细节，而这些细节并不能代表数据的真实分布规律，导致模型在面对新数据时无法准确预测。
原因：模型过于复杂，学习了训练数据中的噪声和细节，而这些细节并不能代表数据的真实分布规律，导致模型在面对新数据时无法准确预测。
解决方法：
- 增加训练数据数
- 使用正则化约束
- 提前结束训练

2.2 欠拟合

定义：模型没有足够的能力去拟合数据的真实规律，即使在训练数据集上也表现不佳，无法捕捉到数据中的关键特征和关系。
原因：模型过于简单，或者训练数据量不足、质量不好等，导致模型无法学习到数据中的复杂模式。
解决方法：
- 增加训练时长
- 增加更多特征
- 增加模型复杂度

二、PR曲线

1. 概念

PR 曲线是以精确率（Precision）为纵轴、召回率（Recall）为横轴所绘制的曲线。在二分类问题中，对于不同的分类阈值，模型会产生不同的精确率和召回率，将这些对应点连接起来就形成了 PR 曲线。

1.1 精确率：预测为正例的样本中真正正例的比例

$Precision=\frac{TP}{TP+FP}$

1.2 召回率：真正正例被预测为正例的比例

$Recall=\frac{TP}{TP+FN}$

真实情况	预测结果
真实情况	正例	反例
正例	TP（真正例）	FN（假反例）
反例	FP（假正例）	TN（真反例）

2. 绘制步骤

2.1 准备数据

2.2 排序预测结果

2.3 计算精确率与召回率

2.4 绘制PR曲线

2.5 计算PR AUC

三、ROC曲线

1. 概念

ROC 曲线是以真正例率（True Positive Rate，TPR）为纵轴、假正例率（False Positive Rate，FPR）为横轴绘制的曲线。对于不同的分类阈值，计算出相应的 TPR 和 FPR，将这些点连接起来就形成了 ROC 曲线。

1.1 真正例率（TPR）：即召回率，反映了模型正确识别正例的能力

$TPR=\frac{TP}{TP+FN}$

1.2 假正例率（FPR）：假正例占负例的比例，反映了模型将负例错误识别为正例的概率

$FPR=\frac{FP}{FP+TN}$

真实情况	预测结果
真实情况	正例	反例
正例	TP（真正例）	FN（假反例）
反例	FP（假正例）	TN（真反例）

2. 绘制步骤

2.1 准备数据

2.2 排序预测结果

2.3 计算真正率与假正率

2.4 绘制ROC曲线

2.5 绘制对角参考线

2.5 计算PR AUC

四、绘制PR曲线图像和ROC曲线图像

导入所需的库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

利用Scikit-learn机器学习库中的函数，生成了一个包含5000个样本和2个类别的数据集，为训练和评估机器学习模型提供训练集。并对数据进行划分训练集与测试集。
```
X, y = make_classification(n_samples=5000, n_classes=2, random_state=42)
 
print("x:")
print(X)
print("y:")
print(y)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
```
使用LogisticRegression 类构建一个逻辑回归模型，并将其命名为 model。然后，使用训练集数据 X_train 和对应的标签 y_train 来训练模型。逻辑回归算法通过拟合一个S形曲线（也称为逻辑函数）来预测二分类问题中的类别。
```
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)
```
使用训练好的模型对测试集样本进行预测，得到每个样本为正例的概率值。然后，使用NumPy中的argsort函数对预测概率进行排序，并将排序结果保存到sort_indices中。[::-1]表示倒序排列，即从大到小排列。通过将测试集的真实标签y_test按照与sort_indices相同的顺序进行排序，得到y_test_sorted得到按照预测概率从高到低排列的测试集样本及其对应的真实标签。接着计算正例个数与负例个数。
```
y_scores = model.predict_proba(X_test)[:, 1]

sort_indices = np.argsort(y_scores)[::-1]
y_test_sorted = y_test[sort_indices]
y_scores_sorted = y_scores[sort_indices]

num_positives = np.sum(y_test)
num_negatives = len(y_test) - num_positives
```
接下来PR曲线与ROC曲线绘制方法不同

PR曲线

1. 初始化PR曲线的变量，遍历不同阈值，通过公式P=TP/(TP+FP)计算精确率与R=TP/(TP+FN)计算召回率，并计算PR曲线下面积。

precisions = []
recalls = []

for i in range(len(y_scores_sorted)):
    threshold = y_scores_sorted[i]
    y_pred = np.where(y_scores_sorted >= threshold, 1, 0)
    
    true_positives = np.sum(np.logical_and(y_pred == 1, y_test_sorted == 1))
    false_positives = np.sum(np.logical_and(y_pred == 1, y_test_sorted == 0))
    
    precision = true_positives / (true_positives + false_positives)
    recall = true_positives / num_positives

    precisions.append(precision)
    recalls.append(recall)

pr_auc = np.trapz(precisions, recalls)

2. 根据数据绘制PR曲线图

plt.plot(recalls, precisions, color='blue', label=f'PR Curve (AUC={pr_auc:.2f})')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('PR')
plt.legend(loc='lower left')
plt.show()

ROC曲线

1. 初始化ROC曲线的变量，遍历不同阈值，计算对应的真正例率和假正例率，并计算ROC曲线下面积。

tpr = [0]
fpr = [0]

for i in range(1, len(y_scores_sorted)):
    threshold = y_scores_sorted[i]
    y_pred = np.where(y_scores_sorted >= threshold, 1, 0)
    
    true_positives = np.sum(np.logical_and(y_pred == 1, y_test_sorted == 1))
    false_positives = np.sum(np.logical_and(y_pred == 1, y_test_sorted == 0))
    
    tpr.append(true_positives / num_positives)
    fpr.append(false_positives / num_negatives)

roc_auc = np.trapz(tpr, fpr)

2. 根据数据绘制ROC曲线图

plt.plot(fpr, tpr, color='red', label=f'ROC Curve (AUC={roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC')
plt.legend(loc='lower right')
plt.show()