AtCoder Beginner Contest 388（题解）

A - ?UPC

思路：我们直接输出S字符串的第一个字符+“UPC”即可

#include<bits/stdc++.h>
using namespace std;
string s;
signed main()
{
	cin>>s;
	cout<<s[0]<<"UPC";
	return 0;
}

 B - Heavy Snake

思路：由于数据很小，我们完全可以写一个D*N时间复杂度的代码，每次都去对ai+ti，然后去寻找最大值，然后输出

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,d;
int a[105];
int l[105];
int ans[105];
signed main()
{
	cin>>n>>d;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i]>>l[i];
		ans[i]=a[i]*l[i];
	}
	for(int j=1;j<=d;j++)
	{
		int maxn=0;
		for(int i=1;i<=n;i++)
		{
			maxn=max(ans[i]+(j*a[i]),maxn);
		}
		cout<<maxn<<"\n";
	}
}

 D - Coming of Age Celebration

思路： 思路：我们可以去统计，每个人的每个宝石会在第几年耗尽，f[i]表示第i年宝石耗尽的人的个数，然后跑一个前缀和，找到第i年耗尽宝石的个数，然后a[i]+i-1-f[i-1]-(n-i)然后和0去最大值就是当前人拥有宝石的个数

#include <bits/stdc++.h>  
using namespace std;  
#define int long long  
int n;  
int a[500005];  
int f[2000005];  
signed main() 
{  
    cin >> n;  
    int cnt = 0;  
    for (int i = 1; i <= n; i++) 
	{  
        cin >> a[i];  
    }  
    for(int i=1;i<=n;i++)
    {
    	f[i+a[i]+(i-1)-cnt]+=1;
    	cnt+=f[i];
	}
	for(int i=1;i<=n;i++)
	{
		f[i]+=f[i-1];
	}
	for(int i=1;i<=n;i++)
	{
		cout<<max(0LL,a[i]+(i-1)-f[i-1]-(n-i))<<" ";
	}
    return 0;  
}

现在来讲一个系列的CEG 

C - Various Kagamimochi

 思路：倒序遍历，直接用upper_bound去寻找大于当前元素一半的下标，然后-1就是最终结果

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[500005];
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	int ans=0;
	for(int i=n;i>=2;i--)
	{
		int flag=a[i]/2;
		int pos=upper_bound(a+1,a+1+n,flag)-a;
		ans+=pos-1;
	}
	cout<<ans;
	return 0;
}

E - Simultaneous Kagamimochi

 思路：假设我们可以做出来k个叠糕，那么必然是最小的那一部分，和最大的那一部分的叠起来的，因此我们可以去二分k的值，然后去进行一个暴力遍历k，当i>=1&&i<=k时，a[i]*2<=a[n-k+i],一但出现不符合的就返回false，否则返回true,时间复杂度为nlogn，刚好可以

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[500005];
bool check(int k)
{
	int flag=1;
	for(int i=1;i<=k;i++)
	{
		int x=a[i+n-k]/2;
		if(a[i]>x)
		{
			flag=0;
		}
	}
	if(flag==1)
	return true;
	else
	return false;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	int l=0,r=n/2;
	int ans=0;
	while(l<r)
	{
		int mid=(l+r+1)/2;
		if(check(mid))
		{
			ans=mid;
			l=mid;
		}
		else
		{
			r=mid-1;
		}
	}
	cout<<ans;
	return 0;
}

G - Simultaneous Kagamimochi 2

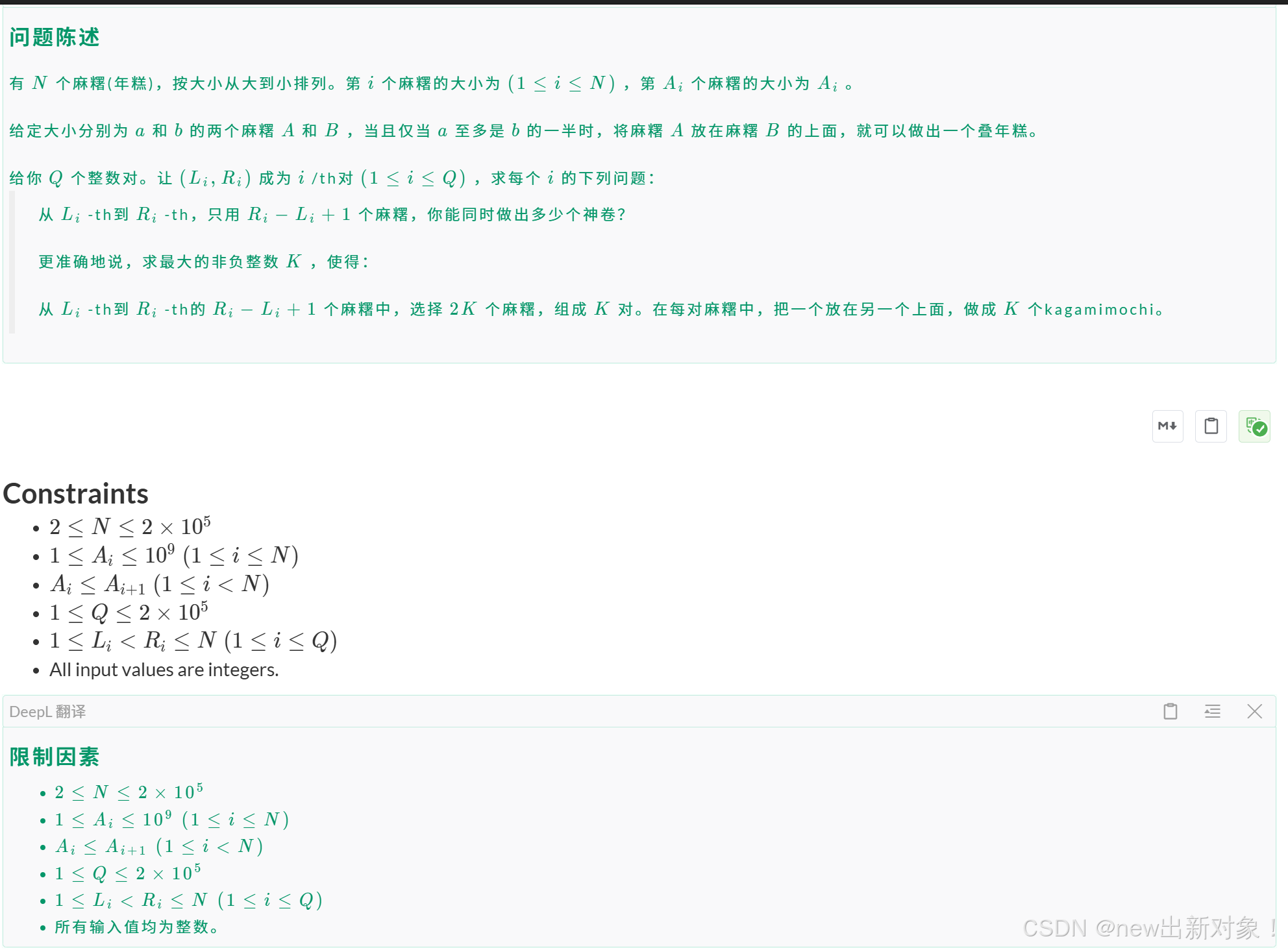
 思路：这题相当于是e题的数据的加强版，相当于问你q个类似于e题的问题，这时候假如还用e题的思路来做那么时间复杂度为q*n*logn，很明显是过不去的，因此我们需要优化一下，q是不能变的，logn的二分也没法继续优化了，因此我们可以选择将那个n优化为O(1)或者说O(logn)级别的时间复杂度，因此我们可以想到用st表去维护，可以实现O（1）时间复杂度的查询

我们的优化想到之后，可以去考虑一下如何去实现，首先我们来分析一下，要满足条件的话，假设我们输入的是L和R，假设我们此时二分的长度k，那么则应该有i>=L&&i<=L+k-1，那么对应则有
a[i]*2<=a[R-k+1-L+i],由c题我们可以知道，我们可以先去求出来每个点的最大的组成叠糕的下标posi，然后去将其变成i-posi，统计与前面的可组成的最大距离（因为如果最大距离，满足了，那么小的距离肯定也能满足形成叠糕），然后用st表去维护一个区间内的最大距离，然后去判断这个距离是否小于后面一段的左端点距离L的距离（标准的比较的点之间的距离），如果小于等于，那么就是可以满足的，否则就是false

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,q;
int a[200005];
int L,R;
int pos[200005];
int st[200005][18];
int check(int l,int r)
{
	int k=log2(r-l+1);
	return max(st[l][k],st[r-(1<<k)+1][k]);
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=n;i++)
	{
		int flag=a[i]/2;
		int p=upper_bound(a+1,a+1+n,flag)-a-1;
		pos[i]=p;
	}
	for(int i=1;i<=n;i++)
	{
		st[i][0]=i-pos[i];
	}
	for(int j=1;j<=17;j++)
	{
		for(int i=1;i+(1<<j)-1<=n;i++)
		{
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
		}
	}
	cin>>q;
	for(int i=1;i<=q;i++)
	{
		cin>>L>>R;
		int l=0;
		int r=(R-L+1)/2;
		int ans=0;
		while(l<r)
		{
			int mid=(l+r+1)/2;
			if(check(R-mid+1,R)<=R-L+1-mid)
			{
				ans=mid;
				l=mid;
			}
			else
			{
				r=mid-1;
			}
		}
		cout<<ans<<"\n";
	}
	return 0;
}