C语言学习之路__青蛙跳台问题

最新推荐文章于 2025-06-06 18:46:55 发布

原创最新推荐文章于 2025-06-06 18:46:55 发布

· 482 阅读

7 ·

版权

文章标签：

#学习 #c语言

文章探讨了一只青蛙跳上n级台阶的跳法问题，发现其与斐波那契数列的关系，通过递归函数实现，随后指出递归效率低下，提倡使用循环改进。作者分享了学习过程中的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一只青蛙可以跳上一级台阶，也可以跳上两级台阶。求该青蛙跳上一个n级台阶总共有多少种跳法？

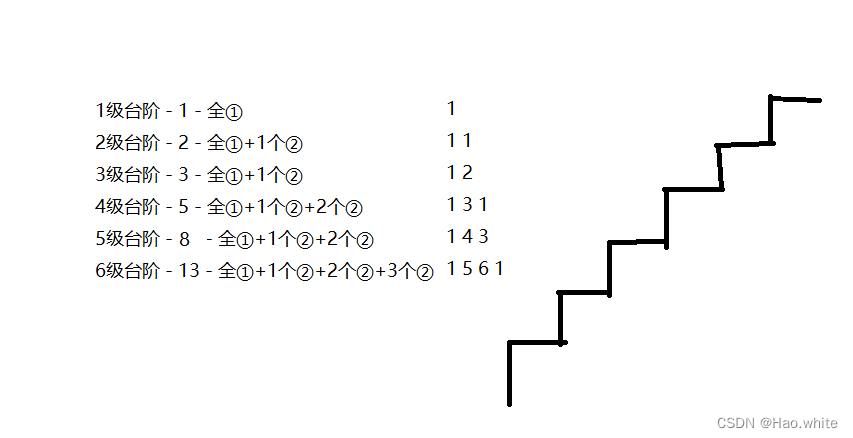
通过找规律发现：青蛙跳上n级台阶的跳法=跳上（n-1）级台阶的跳法+跳上（n-2）级台阶的跳法；俺到这里就惊讶的发现，这不就是斐波那契数列吗？

但为什么是这样的规律呢？俺也甚是疑惑，于是上网看了大佬们的一些说法，其中一种是这么说的：青蛙跳上n级台阶一共有 $f(n)$ 中跳法，无论青蛙怎么跳，最后跳的那一次无非就两种情况，一种是跳一级台阶，一种是跳两级台阶；

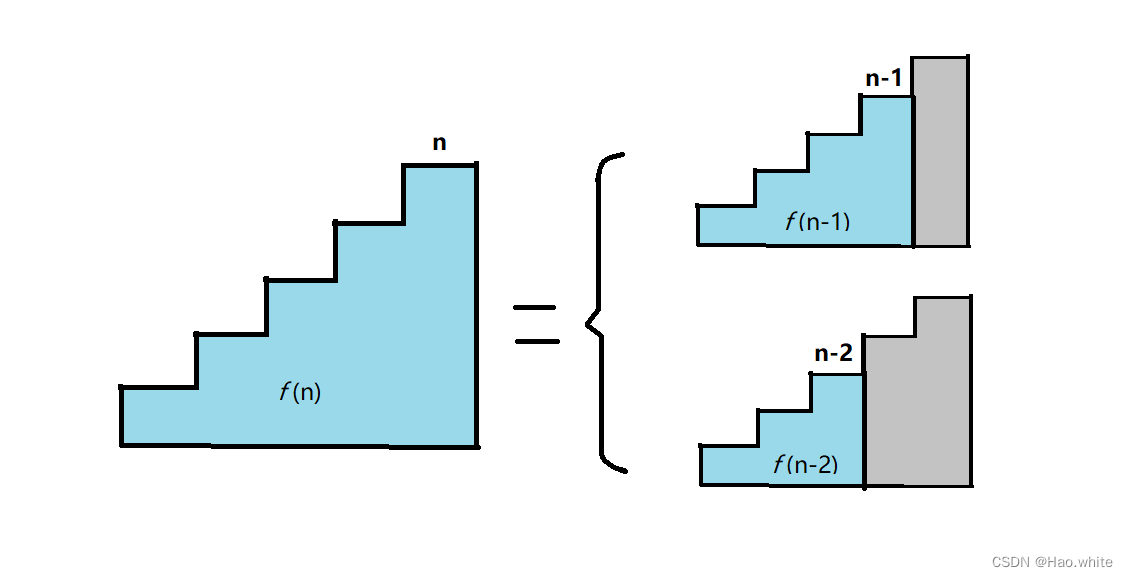
当只剩下一级台阶时：前面的n-1个台阶一共有 $f(n-1)$ 种跳法

当剩下两级台阶时，前面的n-2个台阶一共有 $f(n-2)$ 种跳法

这样一看，确实就解决了斐波那契数列和青蛙跳台问题之间的联系：

#include<stdio.h>

int jump(int n)
{
	if (n - 1 > 0)
		return jump(n - 1) + jump(n - 2);
	else
		return 1;
}

int main()
{
	int n = 0;
	scanf("%d", &n);//台阶数
	int ret = jump(n);
	printf("青蛙跳上%d级台阶一共有%d种跳法", n, ret);
}

因为函数的重复调用，递归明显是一种效率低下的方法；在这里使用循环会好一些！

博客仅作为俺学习过程的记录！