图是数据结构中相对来说比较难的知识点,不过也不用怕,因为都是相对的难ƪ(˘⌣˘)ʃ而已
其次,在企业面试中很少会问图的知识点(问的很少,但也不代表不会问),所以放轻松哦~~
目录
定义:
图不是我们字面意思理解的是一张图,数据结构中的图实际上是由顶点(vertex——V)和顶点之间的关系(edge——E)组成的一种数据结构。
一、顶点(vertex)
下面这个就是一个图:

图中的字母A、B、C、D就是顶点(vertex)
二、边(edge)
如图,节点之间有一条连线,连线代表一个顶点可以到达这条线指向的相邻的顶点:

图中每个字母之间的连线就是边(edge),它可以描述相邻节点之间的关系
比如,A和C之间有一条边连在一起,说明A可以直接到达B,B也可以直接到达A。
但是E不能直接到达D,
因为E和D之间没有连线,
不过可以通过路径E->C->D方式间接到达。
那么图中的weight是什么呢?
学过哈夫曼树,我们都知道代权路径长度这个概念,实际上weight也是这个意思。
图这个数据结构中,可以给每一条边附加一个权值(weight)。
比如所给例子中,A和C之间的边的权值就是9。
在图中,权值可以加也可以不加。
不过,一般我们今后涉及的不管是考试还是面试大部分都是代权的。
图的专业术语以及概念
这些概念看上去很简单,
其实一点都不难理解。
一、有向图和无向图
1、无向图:
刚才在介绍顶点的时候给的图的例子,就是无向图,既:
一个边之间任意一个顶点,可以通过另一个顶点。
比如,A可以到C,C也可以到A。
他们是没有方向的。
2、有向图:
实际上就是限制了边的方向,如图:

每个顶点之间不在是用简单的线段来连接了,而是用箭头。
比如:
顶点1和顶点2,用一个单向箭头连接在一起了,说明1可以通过2,但是2不能通过1
顶点0和顶点1,用两个单向箭头,因此两个顶点可以相互访问。
二、无向完全图和有向完全图
1、无向完全图
定义:
在无向图中有N个节点,若这个图有N*(N-1)/2个边,那么就是一个无向完全图。
上述定义很抽象,下面我们来形象理解(保准一次看懂):
如果图中任意两个节点(顶点节点一样咧,直到说的是vertex(顶点)就行)之间有且仅有一条边,那么就是无向完全图!
如图,就是一个无向完全图:

那么为啥一定要是N*(N-1)/2条边呢?
其实也很好理解,既然要保证每个顶点之间有且仅有一条边,那么从第一个节点开始连线(边),就应该每个节点都连接一次,也就是N-1条边
然后接下来每到一个顶点,连接的边就少一条。
所以总边数就是一个首项为N-1,尾向为0,公差为-1的等差数列。
求和公式一算,就是N*(N-1)/2了。
2、有向完全图
理解了无向完全图,那么有向完全图就简单了。
定义:
在n个顶点的有向图中,若有n * (n-1)条边,
即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图
如图:
三、邻接顶点
在无向图中:
若一条边连接两个顶点u和v,那么u和v互为邻接顶点。
并称这条边依附于顶点u和顶点v。
在有向图中:
若一条边从u连到v(有方向的),那么称u节点邻接到v节点,v节点邻接自u节点。
并称边<u,v>与顶点u和顶点v相关联。
四、顶点的度
定义:
一个顶点v的度是指与它相关联的边的条数,记作deg(v)
在有向图中:
顶点的度等于该顶点的入度与 出度之和;
其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);
顶点v的出度是以v为起始点的有向 边的条数,记作outdev(v)。
因此:dev(v) = indev(v) + outdev(v)
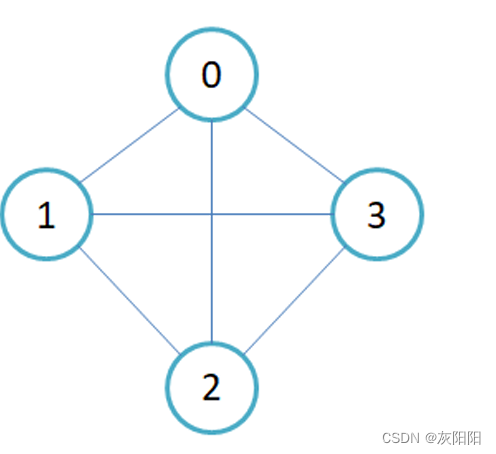
如图,0的度就是二:

无向图中:
这个就简单了,度就是这个顶点的边的个数
如图0这个顶点的度就是三:
五、路径
在一个图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,
则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
六、路径长度
若没有设置边的权重,那么从vi顶点,到vj顶点路径中经过的边的数量就是路径长度。
如果边设置了权重,那么路径长度就是所有边的权值之和。
七、简单路径与回路
若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径:

若路 径上 第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环:

八、连通图与强连通图
连通图是无向图中的概念:
在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。
如果图中任意 一对顶点 都是连通的,则称此图为连通图。
强连通图是有向图的概念:
在有向图中,若任意一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到 vi的路径,则称此图是强连通图。
九、子图/生成图/生成树/最小生成树
1、子图
定义:
对于原来的图G,进行某一些边和顶点的删除,最后所构成的图g,我们就说g是G的一个子图
如图这个例子(只要子图的顶点和边都属于G1,那么就是子图):

第二个例子:
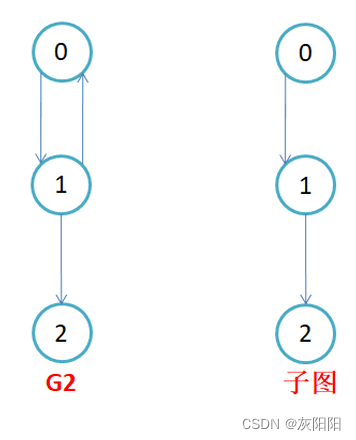
包括这个图,也是G2的子图:

2、生成子图
定义:
只对原来的图的边进行删除,而不删除顶点,所构成的子图就是生成子图(一般简化叫生成图)。
举例子:
对于如下这个图:

只对某一些边进行删除:

这就是一个生成图。
3、生成树
小编先用VN图事先让大家知道一下,图和树的包含关系:

生成树的定义:
只对原来的图G进行边的删除,最后得到的图g:
1、不会形成环,
2、且任意两个顶点,有路径到达,
那么这个图就是生成树。
举例:
原图G:
G的一个生成树(例1):
G的另一个生成树(例2):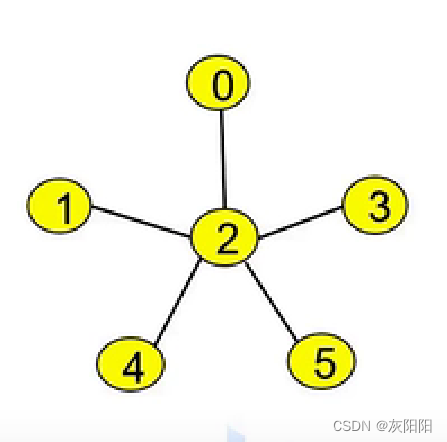
4、最小生成树
定义:
最小生成树,是生成树的一种,区别在于:
1、最小生成树的边的权值之和最小
2、最小生成树的边==N-1(N是图的顶点个数)。
以上两点也是最小生成树的特点,很重要一定要知道,构建最小生成树的算法要用到他们。
注:一个图的最小生成树大概率不唯一。
最小生成树的计算有两个方法:
Kruskal算法
Prime算法
























 1565
1565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








