5.2 简单、高效!5分钟速通凹凸性与拐点 ——《2026李林高数辅导讲义》

 

 

 

4.2.1 讨论曲线曲线的凹凸性与拐点

一.大凹小凸

二.2个解法求拐点:

(1)求出f(x)二阶导，

令f(x)二阶导＝0，

求出x0

(2)证明f(x)二阶导在x0附近异号

注意:如果f(x0)二阶导不存在，且f(x)二阶导在x0两侧异号，则拐点是(x0，f(x0))是拐点

说点干货:

1 .求凹凸区间的时候，求导要三万分细心

2.证明f(x)二阶导在x0异号，就要证明f(x)三阶导存在，且f(x0)此时大概率是在0处。

——————

4.2.2 图形题

图形题掌握的是对概念的熟练程度。

说几个突破点:

1.如果原题有方程，则通过方程变换得到函数的切线方程，然后就是利用“大凹小凸”原理。(大凹小凸是核心)

2.找到零点作为突破点，这时候可能用到“假设法”。

——————

4.2.3 曲率与曲率圆

(1)两个公式:

R＝1/k和k的公式

(2)注意曲线和曲率圆的关系:

在切点处: ①同切线(同斜率)②同曲率

解法:带入函数值+用斜率作为等式+用曲率作为等式，最后联立

——————

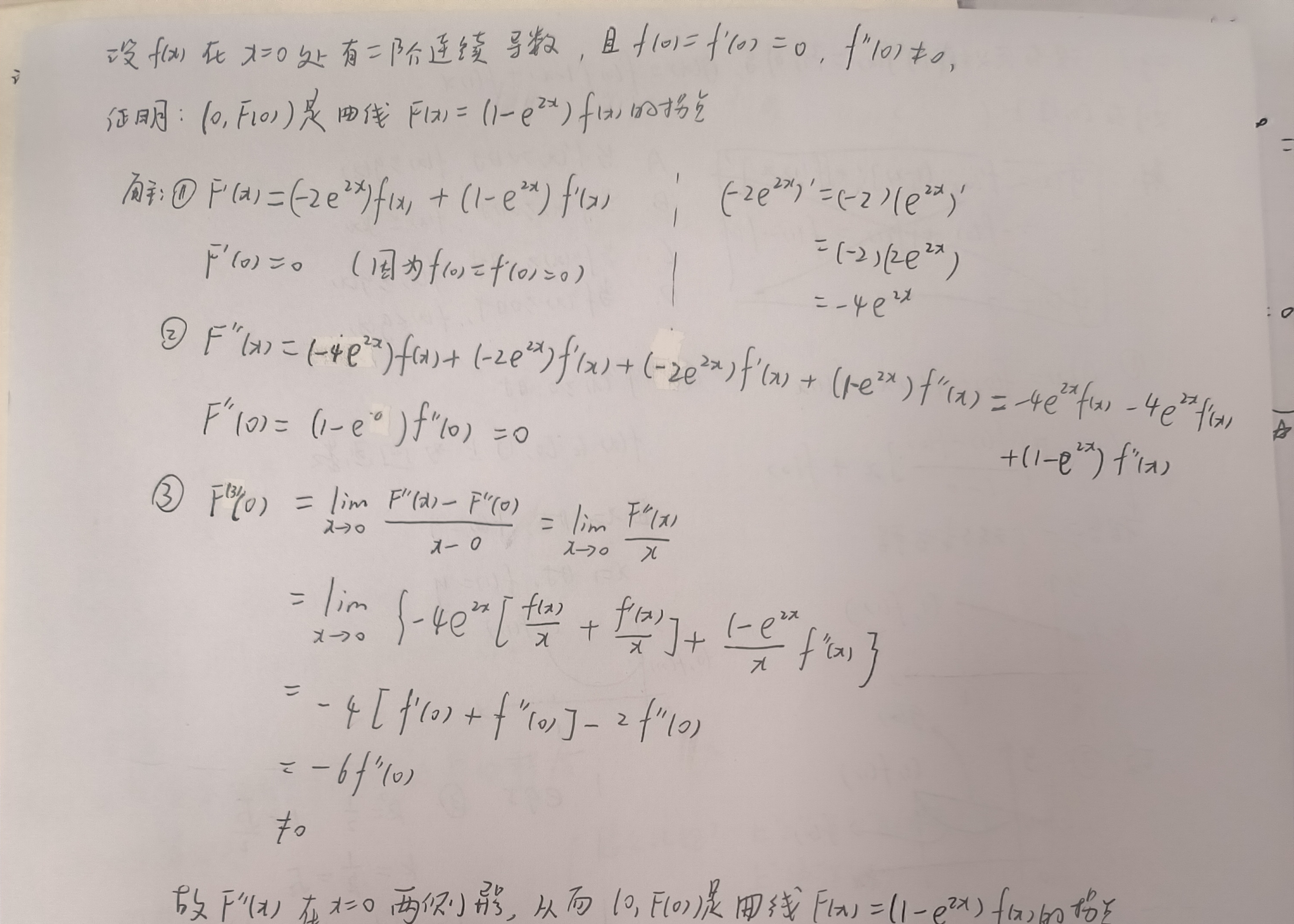
4.2.4 讨论含参方程的根

突破点:极值点+极值+画图分类讨论零点(画图是为了更好判断函数增减趋势)

4.2.5 求渐近线方程

水平渐近线:x→∞ y＝c

铅直渐近线:x→x0 y＝∞

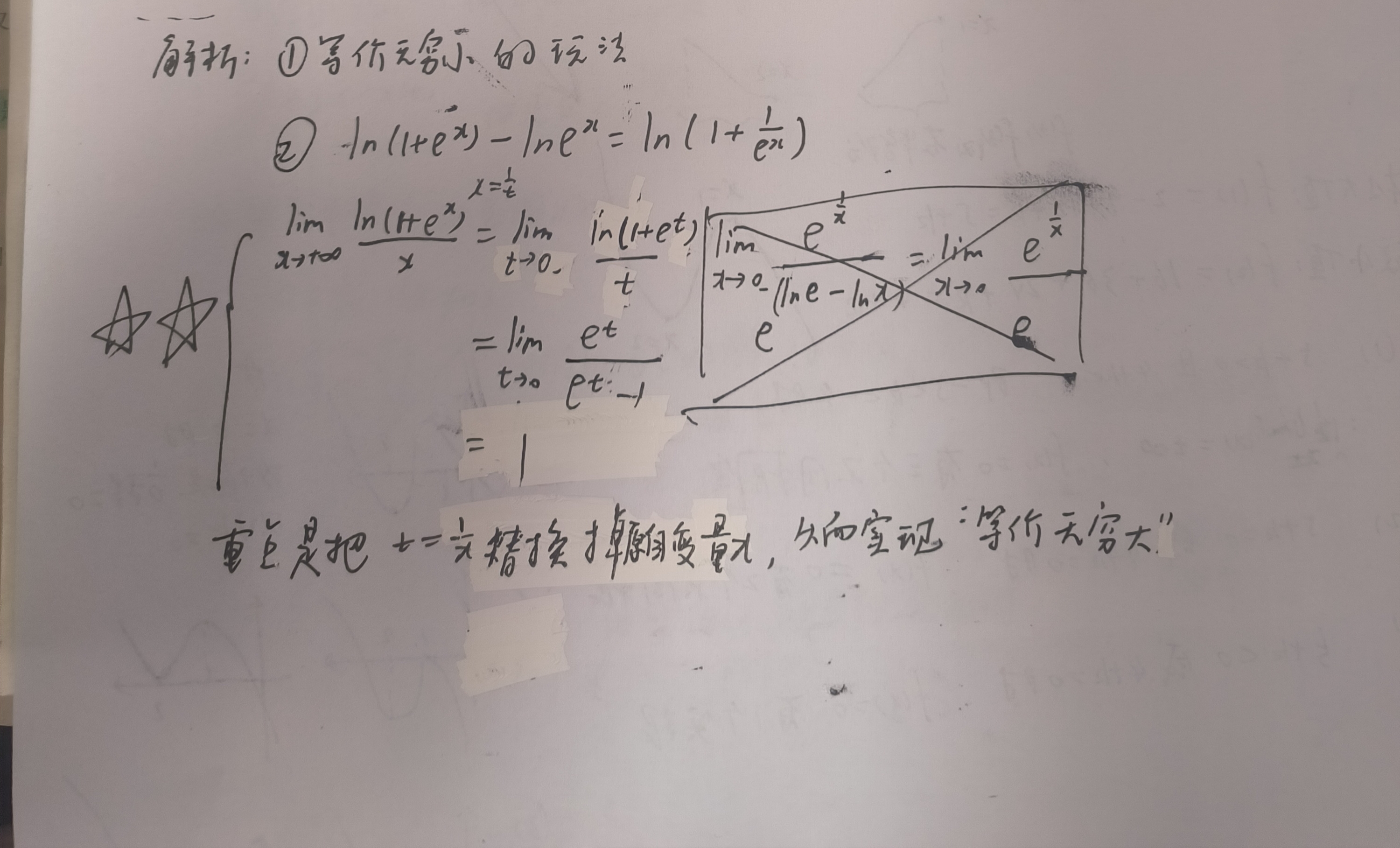
斜渐近线:x→∞ ①y/x＝k ②y-kx＝b

主要间接考察的是等价无穷小，如果出现等价无穷大，就要用t＝1/x替换。