详细介绍三角高程测量（赋计算代码）

做完作业了

已于 2024-01-15 10:26:35 修改

阅读量2.5k

点赞数 27

文章标签：算法 c语言 c++

于 2024-01-15 10:15:03 首次发布

本文链接：https://blog.csdn.net/2301_81723939/article/details/135586184

版权

水准测量局限性：

由图可知，在水准测量时由于受到尺长的限制，不利于坡度较大情况下的高差测量，在此情况下，可采用三角高程测量。

三角高程测量原理：

由此可以看出，测站高程HA为已知值，测站A仪器高 i 以及待测点B仪器高 v 为测量值，平距离 D 及垂直角 α 为观测值。假设 $H_{A}$ = 50, i = 1，v = 1.5，S = 100，α = 45°，则

$H_{B}=50+1+100\times tan45^{\circ}-1.5=149.5$

$H_{A}$ = 50, i = 1，v = 1.5，S = 500，α = 45°，则

$H_{B}=50+1+500\times tan45^{\circ}-1.5=549.5$

远距离三角高程测量：

当距离较远（大于300m）时，考虑地球曲率和大气折光对高差的影响，应对观测得到的高差加上 “ 球差改正 ” 和 “ 气差改正 ” ，即 “ 两差改正 ”。

其中R为地球半径，假设观测距离为500m，那么高差的两差改正为

$f=(1-0.14)\times 0.5\times 0.5\div 2\div 6371.393\approx 0.0000168722915km$ ≈ 17mm

此时A、B两点之间的高差为：

$h_{AB}=Dtan\alpha +i-v+f_{1}+f_{2}$

代码实例：

c语言代码及运行结果如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>
#include <math.h>

#define pi 3.141592653589793238463
#define R 6371.393
#define k 0.14

// 计算高程的函数
double computeElevation(double distance, double angle, double instrumentHeight)
{
    // 计算高程，这里假设三角形的底边与地面平行
    double elevation = distance * tan(angle) - instrumentHeight;

    return elevation;
}

//计算双差改正
double difference(double distance)
{
    double f = (1 - k) * distance * distance / 1000.0/1000.0/ 2.0 / R;
    return f;
}

int main()
{
    // 定义度分秒、或者度数小数形式，即选择参数
    int num,num1;
    double du, fen, miao,jiaodu;
    double dushu;
    // 观测点数据,obsInstrumentHeight-观测站仪器高度，obsheight观测站高程

    double obsInstrumentHeight, obsheight;
    // 观测站计算高度，即观测站高程+观测站仪器高度
    double height;

    // 待测点数据，testDistance-观测距离，testAngle-观测角度，obsInstrumentHeightTest-待测点仪器高，testHeight-待测点高程
    double testDistance, testAngle, testInstrumentHeightTest, testHeight;

    // 输入观测点数据
    printf("观测点数据（高程 仪器高度）：");
    scanf("%lf %lf", &obsheight, &obsInstrumentHeight);

    height = obsheight + obsInstrumentHeight;

    // 输入待测点数据
    printf("待测点数据（边长(m) 待测点仪器高度）：");
    scanf("%lf %lf", &testDistance, &testInstrumentHeightTest);

    // 定义弧度变量
    double radian;

    // 处理输入角度
    printf("输入为度、分、秒的形式选择1，输入为度的小数形式选择2\n");
    scanf("%d", &num);
    if (num == 1)
    {
        scanf("%lf %lf %lf", &du, &fen, &miao);
        // 角度转弧度
        jiaodu = du + fen / 60.0 + miao / 3600.0;
        radian = (jiaodu * pi) / 180;
    }
    else
    {
        scanf("%lf", &dushu);
        // 角度转弧度
        radian = (dushu * pi) / 180;
    }
    printf("是否考虑双差改正：1）考虑 2）不考虑\n");
    scanf("%d", &num1);
    if (num1 == 1)
    {
        // 计算待测点高程
        testHeight = computeElevation(testDistance, radian, testInstrumentHeightTest) + difference(testDistance/1000.0)+height;
    }
    else
    {
        // 计算待测点高程
        testHeight = computeElevation(testDistance, radian, testInstrumentHeightTest) + height;
    }

    // 输出结果
    printf("观测点高程: %.10lf 米\n", obsheight);
    printf("待测点高程: %.10lf 米\n", testHeight);

    return 0;
}

c++代码及运行结果如下：

#include <iostream>
#include <cmath>
#include <iomanip>

#define pi 3.141592653589793238463
#define R 6371.393
#define k 0.14

// 计算高程的函数
double computeElevation(double distance, double angle, double instrumentHeight) 
{
    // 计算高程，这里假设三角形的底边与地面平行
    double elevation = distance * tan(angle) - instrumentHeight;

    return elevation;
}
//计算双差改正
double difference(double distance)
{
    double f = (1 - k) * distance * distance / 1000000.0 / 2.0 / R;
    return f;
}

int main() 
{
    //定义度分秒、或者度数小数形式，即选择参数
    int num,num1;
    double du, fen, miao, jiaodu;
    double dushu;
    // 观测点数据,obsInstrumentHeight-观测站仪器高度，obsheight观测站高程

    double obsInstrumentHeight , obsheight;
    //观测站计算高度，即观测站高程+观测站仪器高度
    double height;

    // 待测点数据，testDistance-观测距离，testAngle-观测角度，obsInstrumentHeightTest-待测点仪器高，testHeight-待测点高程
    double testDistance, testAngle, testInstrumentHeightTest, testHeight;

    // 输入观测点数据
    std::cout << "观测点数据（高程 仪器高度）：";
    std::cin >> obsheight >> obsInstrumentHeight;

    height = obsheight + obsInstrumentHeight;

    // 输入待测点数据
    std::cout << "待测点数据（边长 待测点仪器高度）：";
    std::cin >> testDistance  >> testInstrumentHeightTest;

    //定义弧度变量
    double radian;

    //处理输入角度
    std::cout << "输入为度分秒的形式选择1，输入为度的小数形式选择2\n";
    std::cin >> num;
    if (num == 1)
    {
        std::cin >> du >> fen >> miao;
        //角度转弧度
        jiaodu = du + fen / 60.0 + miao / 3600.0;
        radian = (jiaodu * pi) / 180;
    }
    else
    {
        std::cin >> dushu;
        //角度转弧度
        radian= (dushu * pi) / 180;
    };
    std::cout << "是否考虑双差改正：1）考虑 2）不考虑\n";
    std::cin >> num1;
  
    if (num1 == 1)
    {
        // 计算待测点高程
        testHeight = computeElevation(testDistance, radian, testInstrumentHeightTest) + difference(testDistance/1000.0)+height;
    }
    else
    {
        // 计算待测点高程
        testHeight = computeElevation(testDistance, radian, testInstrumentHeightTest) + height;
    }

    // 输出结果
    std::cout << "观测点高程: " << obsheight << " 米\n";
    std::cout << std::fixed;
   /* std::cout << "待测点高程: " << testHeight << " 米\n";*/
    std::cout << "待测点高程: " << std::setprecision(6) << testHeight << " 米" << std::endl;

    return 0;
}

注：为什么这里考虑两差改正后结果并没有变，主要是因为这里假设的观测距离为500，0.5km，

计算两差改正 f = ( 1 - 0.14 ) * 0.5 * 0.5 ÷ 6371.393 ÷ 6371.393 ÷ 1000 = 0.0000000000052，改正数太小了，所以没有显示。（最后除以1000是把单位为km转换成米。）

多传递点三角高程测量（数据批处理）：

当待测点高度过高或与已知高程点距离过远时，那么仍然需要设置若干穿点用来传递高程，如下：

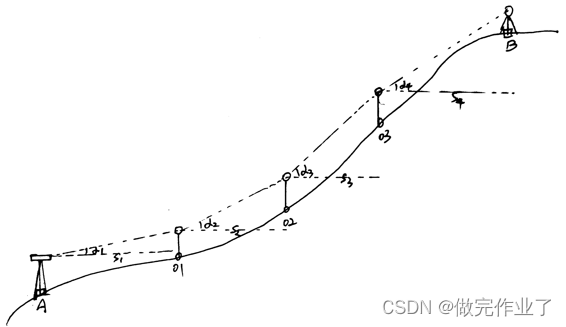
从图中可以看出，若要从已知高程点 A 测得 B 点高程，中间加了三个转点，且当在A点观测完后，需要记录 A 点的仪器高、01点的觇标高、水平距离S1、垂直角α1。在观测记录后将观测仪器从A点放置在01点转点位，将觇标放置在02点继续观测，依次类推直至觇标放置在B点，最后根据已知点 A 的高程加上各测段计算后的高差最终求出 B 点高程。

因此在输入的文本文件中，前四行为控制信息，

第一行为已知点 A 的高程；

第二行为转点数目（可以发现当有三个转点时会有四次观测）；

第三行为选择角度的输入形式，如果为1，则是以度、分、秒的形式处理，如果为2则以度的小数形式输入；

第四行选择是否考虑两差改正，如果为1则考虑，为2，不考虑。

    // 读取起始点A的高程
    fscanf(inputFile, "%lf", &height_A);

    // 读取转点数目
    fscanf(inputFile, "%lf", &num);

    // 读取角度形式
    fscanf(inputFile, "%d", &num1);

    //读取是否考虑两差改正
    fscanf(inputFile, "%d", &num2);

从第5行开始为每一站的观测值，代码每读取一行则处理一站结果，

如果输入文件第三行控制角度输入形式为1，则第五行开始观测值每行有六个数字，分别为观测的水平距离、度、分、秒、观测站仪器高、觇标高，且每个数字中间以空格分隔。

fscanf(inputFile, "%lf %lf %lf %lf %lf %lf", &guanceS, &du, &fen, &miao, &yiqigao1, &yiqigao2);

如果输入文件第三行控制角度输入形式为2，则第五行开始观测值每行有四个数字，分别为观测的水平距离、度的小数形式、观测站仪器高、觇标高，且每个数字中间以空格分隔。

fscanf(inputFile, "%lf %lf %lf %lf", &guanceS, &dushu, &yiqigao1, &yiqigao2);

两种不同格式的输入文本文件示例如下：（注意这是两种不同格式的文件）

运行程序，输入定义好的文本文件名，则直接在该路径下生成结果文件。

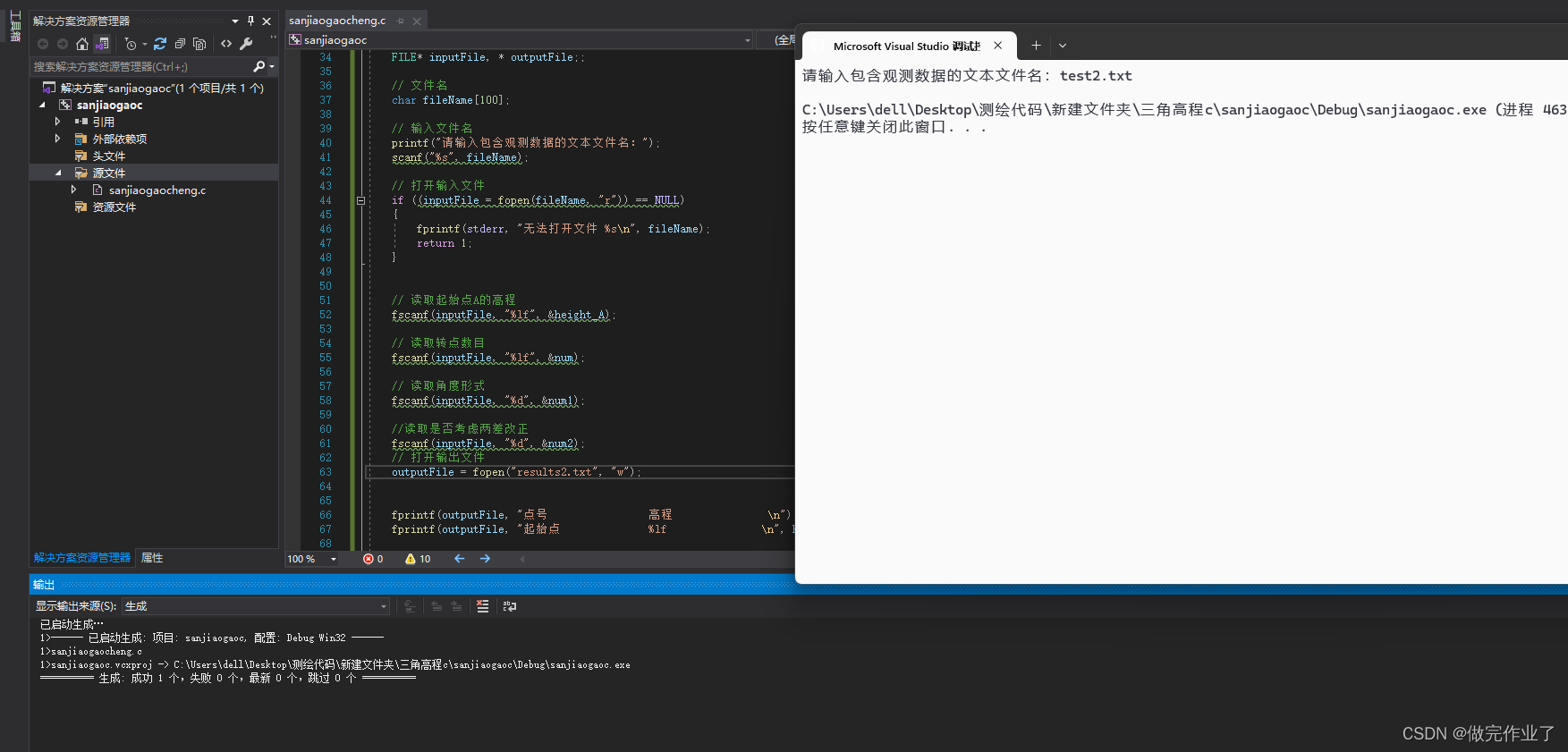
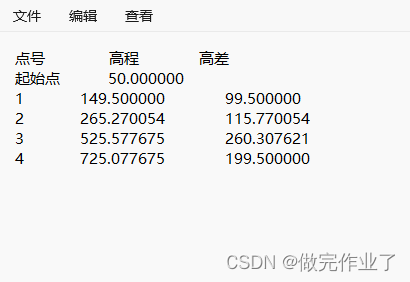
注意：在此处修改输出文件名，当处理多个数据文件时，每次都要对输出文件名进行修改。

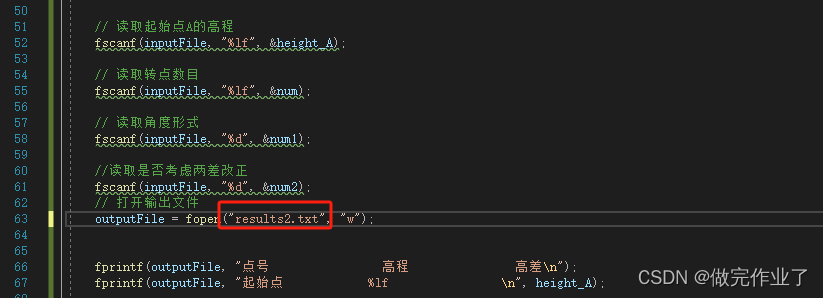
而c++批处理代码输出结果文件在此处进行更改：

c语言批处理代码三角高程测量批处理源码(c语言)资源-CSDN文库

c++批处理代码三角高程测量数据批处理源码(c++)资源-CSDN文库

三角高程测量特点：

① 三角高程测量两点距离较远时，应考虑加地球曲率和大气折光影响的改正（两差改正）；

② 两点间对向观测高差取平均，能抵消两差影响；

③ 三角高程测量通常组成附合或闭合路线，以检验观测精度；

④ 用电子全站仪进行三角高程测量，能代替三、四等水准测量。

影响三角高程测量精度的因素：

① 竖直角测量误差：竖直角观测时，通过盘左、盘右观测取平均值可以降低仪器误差的影响。

② 边长测量误差：在利用测距仪观测边长时，一定要检测棱镜常数、温度、气压等参数的设置，棱镜常数要与棱镜类型一致，保障测距精度。

③ 仪器高和觇标高测量误差。

④ 大气折光影响：通过直、反觇观测高差，取其平均值作为测量高差，可以降低球气差影响。