概率图模型—因子图

最新推荐文章于 2025-02-07 17:41:27 发布

星空汉堡包

最新推荐文章于 2025-02-07 17:41:27 发布

阅读量1.8k

点赞数 9

文章标签：笔记

本文链接：https://blog.csdn.net/2302_76592767/article/details/137785075

版权

本文介绍了因子图作为一种表示概率模型中变量和因子关系的工具，强调了其与贝叶斯网络的差异，以及如何将贝叶斯网络转化为因子图并进行变量消元以求解边缘概率。内容包括因子图的结构、转换示例和变量消元方法的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

因子图（Factor Graph）是一种用于表示概率模型中的变量和因子之间关系的图结构。在概率论和统计中，因子通常指的是变量的函数，这些函数用于描述变量之间的依赖关系或概率分布。因子图通过图形化的方式展示了这些变量和因子之间的相互作用，从而提供了一种直观和灵活的工具来理解和分析复杂的概率模型。

在因子图中，变量通常表示为节点，而因子则通过边与这些变量节点相连。这些边表示了因子与变量之间的依赖关系。因子图的一个重要特点是它可以清晰地展示出概率模型中各个部分之间的独立性关系，这有助于简化计算和提高推理效率。

与贝叶斯网络相比，因子图提供了更大的灵活性。贝叶斯网络主要关注于条件概率的表示，而因子图则可以更一般地表示概率分布的分解。因此，在某些情况下，因子图可能更适合用于描述和分析概率模型。

因子图是二部图，包括两类节点：1、所有的变量节点；2、概率分布的每个局部因子对应一个节点。为了区分这两类节点，一般用方形节点表示因子节点（即 $f_s$ ）。

因子图边的定义规则为：对于同一类节点，它们之间没有边；每个因子节点 $f_s$ 与 $X_s$ 中的所有变量节点相连。

例一：贝叶斯网络 $p(x) = p(x_1)p(x_2)p(x_3\mid x_1,x_2)p(x_4\mid x_1,x_3)$

其对应的因子图如图所示：

其中 $f_a(x_1)=p(x_1),f_b(x_2)=p(x_2),f_c(x_3,x_1,x_2)=p(x_3\mid x_1,x_2),f_d(x_4,x_1,x_3)=p(x_4\mid x_1,x_3)$

可以看出，因子图是将因子和对应与之相关的变量用边连接起来。

例题：

已知以下贝叶斯网络，包含 7 个变量，即 Season (季节), Flu (流感), Dehydration (脱水), Chills (发冷), Headache (头疼), Nausea (恶心), Dizziness (头晕)。

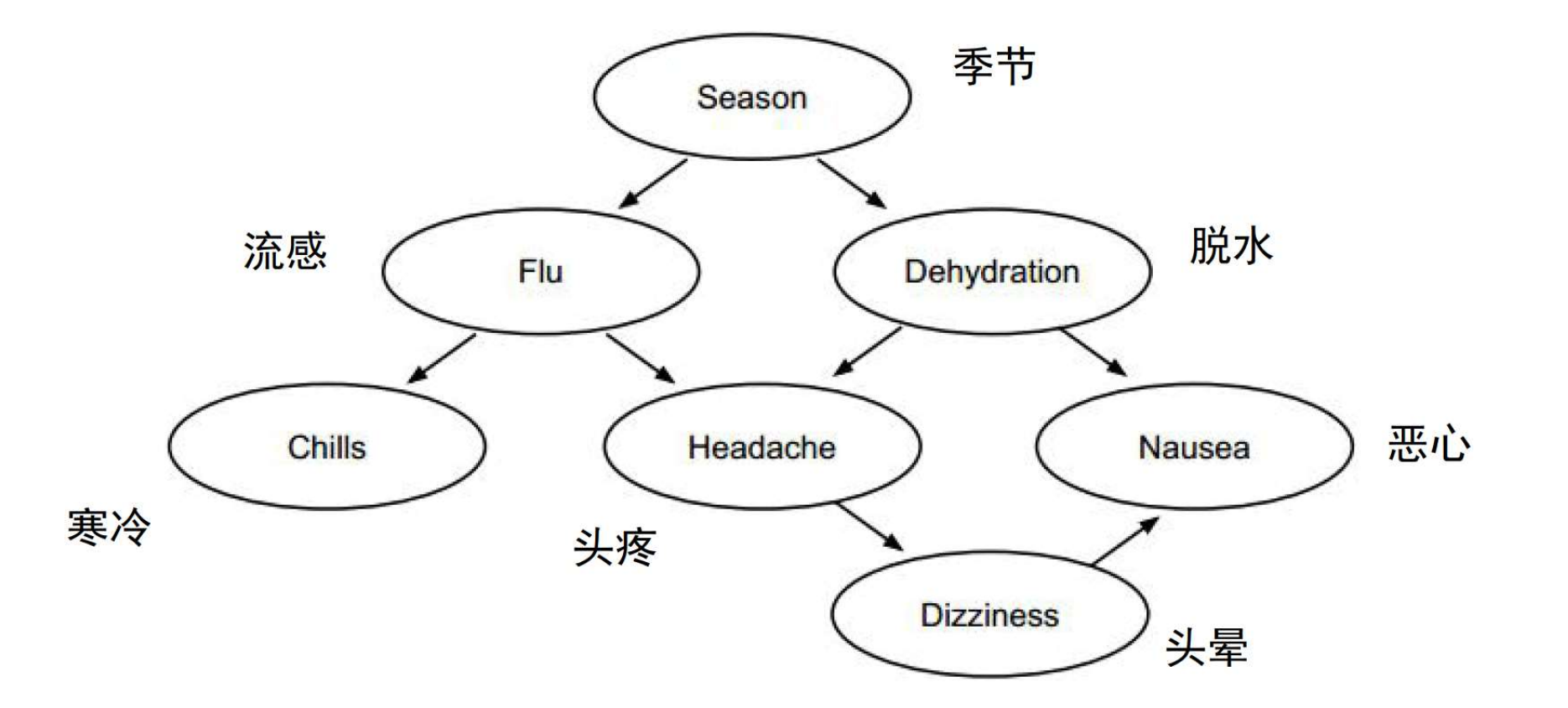
(1) 将以上贝叶斯网络用因子图表示，每个变量节点用首字母表示即可（每个节点用变量首

字母表示，脱水和头晕节点分别用 De 和 Di 表示）。

(2)求解关于变量头晕（Di）的边缘概率？按照启发式的变量消元准则选择消元顺序。

(3)根据求解变量头晕（Di）边缘概率的消元过程，绘制变量消元表格。

(4) 根据上述变量消元表格绘制导出图,并分析计算导出图宽度。

(5)根据上述变量消元表格绘制团树，并展示简化之后的结果。

解答：

（1）这道题的第一题就依据上面的介绍，即可画出对应的因子图

1、先将这个贝叶斯网络转化为公式并化简（熟练的可以直接画）： $p(X)=p(S)p(F\mid S)p(De\mid S)p(C\mid F)p(H\mid F,De)p(N\mid De)p(Di\mid H,N)$

得到的因子图如图所示：

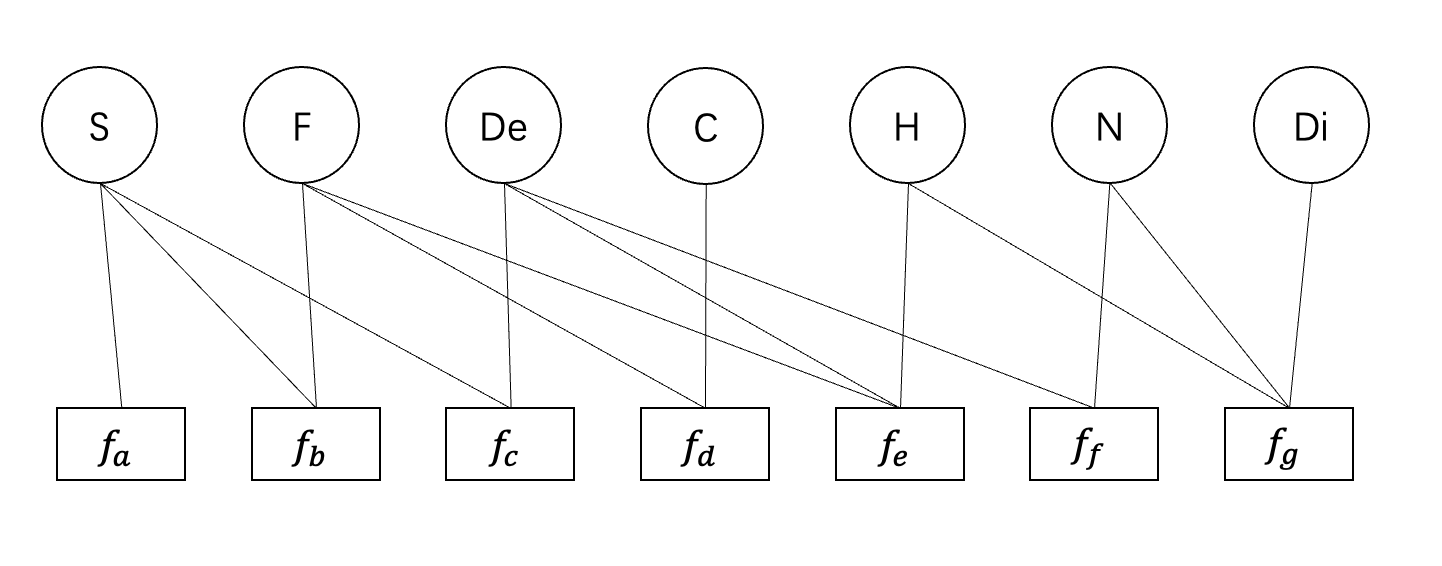
（2）实际推理过程可以根据一些启发式规则来选择消元顺序，如：选择具有最少邻节点的节点进行变量消元。

我选的消元顺序为：C、S、Di、N、F、De（、H）

（3）依据上面的消元顺序绘制变量消元表格

（4）根据每次消元所涉及的变量来绘制导出图，导出图宽度为最大团的节点数减1

（5）我绘制的团树是这个样子的

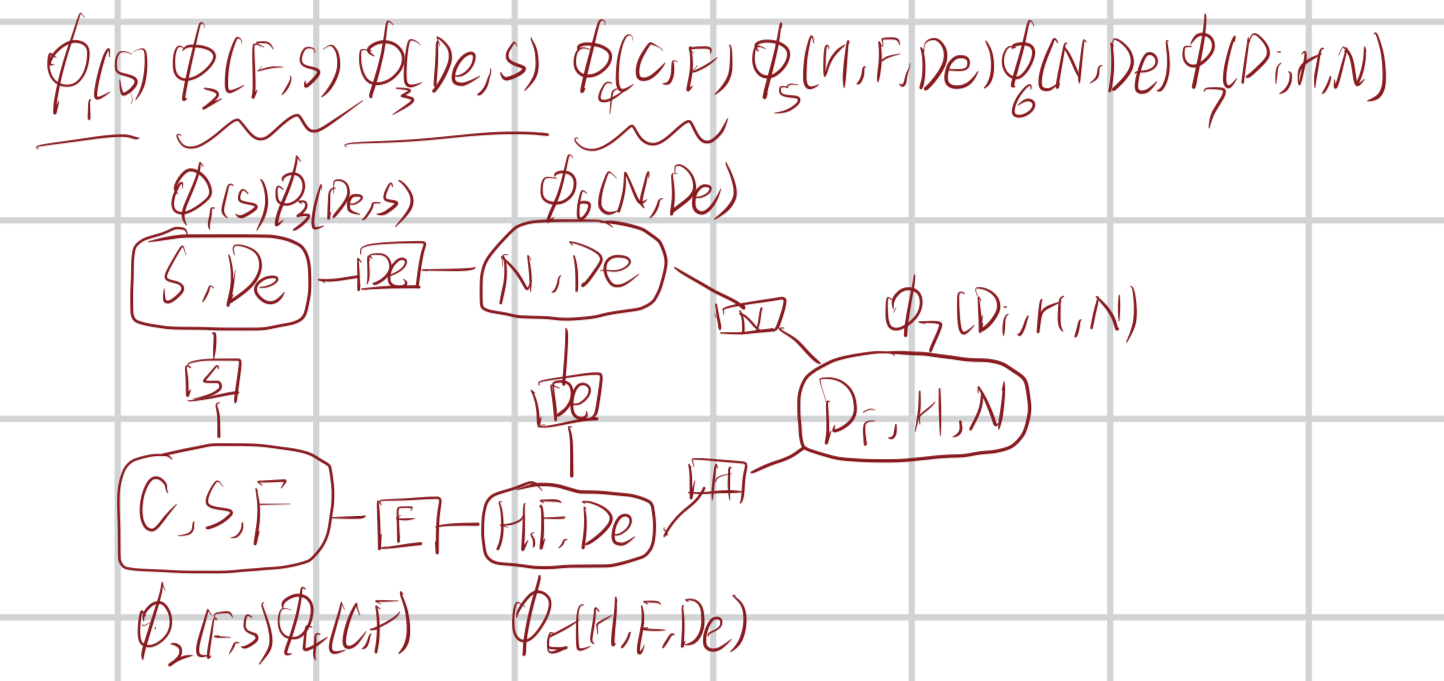
以上仅为作者本人学习时的思考，有错误的地方还请指出。