MATLAB常用语句总结6

记忆力比较差，把学习过程中常用的语法记录于此，方便回忆时索引

MATLAB总结6：随机数以及蒙塔卡罗方法

---

前言

随机数生成是概率中的重要工具，根据大数定律可以用作用频率去趋近概率。而蒙塔卡罗方法可以用作这一趋近的方法。蒙塔卡罗还可以对于不能精确求解的积分问题,做有效的数值计算方法，而且通过大量随机样本来近似积分值,收敛速度不依赖于积分维数

---

一、随机的生成方式

1、随机数

（1）rand

生成[0,1)区间内的均匀分布随机数。

r = rand 		%生成1个随机数
r = rand(m,n) %生成m*n个随机数的矩阵
rand('state',s) %设置随机数生成器的种子为s

示例:

r = rand
R = rand(3,4)

（2）unifrnd

生成指定区间内的均匀分布随机数。

r = unifrnd(a,b) %生成[a,b)区间内的1个随机数
R = unifrnd(a,b,m,n) %生成m*n个[a,b)区间内的随机数矩阵

示例:

r = unifrnd(0,10)
R = unifrnd(-5,5,2,3)

（3）randn

生成标准正态分布(均值0,方差1)的随机数。

r = randn %生成1个标准正态分布随机数
R = randn(m,n) %生成m*n个标准正态分布随机数矩阵
randn('state',s)% 设置随机数生成器的种子为s

示例:

r = randn
R = randn(4,4)

（4）exprnd

exprnd 会生成一个服从指数分布的随机数，指数分布的概率密度函数为 f(x) = λ * exp(-λ*x)，其中 λ 为率参数

示例：

r=exprnd(5);    %生成率参数为5的指数分布

还有很多类似的生成方法，记住rand就行

2、离散型随机变量的生成

可以用rand生成一段区间的离散型变量的概率，其实就是利用频率接近概率的思想
例如：

%生成Y(i)=-1 rand<0.5
%	 Y(i)=1 rand>0.5
N=1000;
X=rand(1,N);
for i=1:N
	if X(i)<0.5
	Y(i)=-1;
	else
	Y(i)=1;
	end
end

首先生成 1000 个服从均匀分布(0,1)的随机数,存储在向量 X 中
然后遍历 X 中的每个元素,如果小于 0.5,则将对应的 Y 元素赋值为 -1,否则赋值为 1
最终 Y 就是一个由 -1 和 1 组成的随机向量,其服从概率为 0.5 的二值分布

---

二、蒙塔卡罗方法

1、定义

蒙特卡罗方法是一种使用随机数或伪随机数来解决计算问题的方法。他的基本思想是
通过随机抽样来模拟复杂的概率过程或随机事件,并进行统计分析得到结果。
利用大量随机样本,通过统计分析来近似求解复杂的数学问题。

例如：采用蒙特卡罗方法估计圆周率

n=input('请输入产生点的个数：');
 m=0;
 for i=1:n
 x=-1+2*rand; y=-1+2*rand;
 if x^2+y^2<=1
 m=m+1;   %如在圆内就统计
end
 end
 mypi=4*m/n

2、用蒙塔卡罗方法优化模型

用蒙特卡罗法求解下列优化模型：

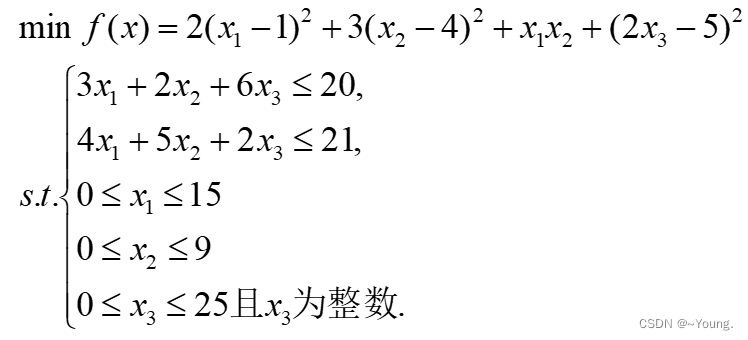
function [betterx,betterval]=fun
% myobj 计算目标函数函数值的Matlab函数句柄
% rndfea 产生一个可行解的Matlab函数句柄
betterx = rndfea;  % 产生一个可行解
betterval = myobj(betterx); %并计算其函数值
for i=1:1e5 % 随机投点
    x= rndfea;%投点
    if myobj(x)<betterval
        betterx=x;
        betterval=myobj(x);
    end
end

function r=myobj(x)
r=2*(x(1)-1)^2+3*(x(2)-4)^2+x(1)*x(2)+(2*x(3)-5)^2;
function c=mycons(x)
c=[3*x(1)+2*x(2)+6*x(3)-20; 4*x(1)+5*x(2)+2*x(3)-21];%检测是否满足前2个约束条件
function x=myrnd
x=[15*rand;9*rand;fix(26*rand)];%在决策变量的边界内投点

function  x=rndfea    %产生一个可行解（满足所有约束条件的点）
	while 1
	    x = myrnd; %
	if mycons(x)<=0
	       return
	end
end

betterx=x;
betterval=F(x);

3、对复杂问题的求解

假设某商场一天的男顾客数服从参数 的泊松分布，女顾客数服从参数 的泊松分布.顾客进商场，可能消费，也可能不消费.若为男顾客，消费的概率为20%，消费额服从区间 的均匀分布；若为女顾客，消费的概率为40%，消费额服从区间 的均匀分布.商场有优惠活动，消费额满300减30元，满500减60元.
请模拟该商场一天的营业额.

分析：对于本题即可采用蒙塔卡罗方法求解，先计算男顾客和女顾客的概率密度，而后计算其购买的概率和金额，再根据相应处的值相乘得到总金额

function incomemax=incoming

lam1 = 100;  %泊松分布的参数
lam2 = 400;
income=[];
x=0:500;
mens = poisspdf(x,lam1);  %概率密度
womens=poisspdf(x,lam2);
subplot(2,2,1);
plot(x,mens); hold on;
plot(x,womens);
legend('男光顾量','女士光顾量');

for x=1:500
        if rand<=0.2    %男士购买概率为0.2
    buy1(x)=unifrnd(200,400);
    else
        buy1(x)=0;
        end
        if rand<=0.4    %%女士购买概率为0.4
    buy2(x)=unifrnd(300,600);
    else
        buy2(x)=0;
    end
    subplot(2,2,2);
    plot(x,buy1(x),'+'); hold on;
    plot(x,buy2(x),'.');
    legend('男士购买量','女士购买量');
    
    if buy1(x)>=300     %对于每个客户的减免
    buy1(x)=buy1(x)-30;
    elseif buy1(x)>=500
        buy1(x)=buy1(x)-60;
    elseif buy2(x)>=300
        buy2(x)=buy2(x)-30;
    elseif buy2(x)>=500
        buy2(x)=buy2(x)-60;
    end
    subplot(2,2,3);
    plot(x,buy1(x),'+'); hold on;
    plot(x,buy2(x),'.');
   legend('男士优惠后购买量','女士优惠后购买量');
    
    income=[income,x*poisspdf(x,lam1)*buy1(x)+ x*poisspdf(x,lam2)*buy2(x)];
end
x=1:500;
subplot(2,2,4);
plot(x,income);

incomemax=sum(income);

绘图结果：