从来没学过这么通透的 - 排列&组合

ん贤

已于 2025-03-13 20:24:32 修改

阅读量1k

点赞数 85

分类专栏：算法文章标签：算法笔记经验分享其他数学建模

于 2025-03-13 15:50:14 首次发布

本文链接：https://blog.csdn.net/2302_80067378/article/details/146222028

版权

算法专栏收录该内容

25 篇文章

订阅专栏

昨天无意间，做了一道算法题，优雅的解法又需要用到组合这种数学知识！

这次，我要狠狠攻克它！

既然如此，那就将排列与组合一块打包学习吧。

注意，这里主要是讲解相关思想，具体算法大家可以到 leetcode、牛客、洛谷等算法平台上搜索。

一、先说说什么是排列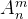 $A_{n}^{m}$ ？

举一个生活中，常见的例子。

现在，有3名学生(A、B、C)排队，要站成一排，请问有几种排法？

所以答案就是 $3\times2\times 1=6$ ，这不就是3的阶乘(3！)吗？

还不理解的，可以看一看图：

在深入探究一点，如果有10名学生，从中选取3名学生，排成一排，请问有几种排法？

所以答案就是 $10\times9\times 8 = 720$ ，这不就是10的阶乘除以7的阶乘吗( $\frac{10!}{7!}$ )吗？

总结一下，于是假设总人数是n人，挑选m人，不就变成了 $n\times(n-1)\times ...\times(m+1)$

也就是 $\frac{n!}{m!}$ 。

所以可以总结出来 $A_{n}^{m}$ = $\frac{n!}{m!}$ 。

小结一下：

为了更严谨，咱们正式一些。

排列：一般的，从n个不同的元素中取出m(m<=n)个元素，按一定顺序排成一排，叫做从n个元素中取出m个元素的一种排列。

排列数：一般的，从n个元素中取出m个元素的所有的排列个数，叫做从n个元素中取出m个元素的排列个数。用符合 $A_{n}^{m}$ 表示。且 $A_{n}^{m}$ = $\frac{n!}{m!}$ 。

二、那什么又是排列数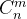 $C_{n}^{m}$ 呢？

就还是那个例子。

现在，有10名学生(A、B、C...)，从中选取3名学生，请问有几种选法？

画重点了！本选择方法，不要求有序！

而上方咱们计算时，为 $10\times9\times 8 = 720$ ，也就是 $A_{10}^{7}$

而其中一共有 $A_{3}^{3}$ 种排序方法（ $3\times2\times1 = 6$ ）

这一相除，不就变成了 $\frac{A_{10}^{7}}{A_{3}^{3}}$ 这个公式吗，也就是720/6=120种。

排列以后，不就变成了这个公式吗！

小结一下：

组合：从n个不同的元素中任意挑选m(m<=n)个元素，组成一组，他就是从n个元素中挑选m个元素的一个组合。

组合数：从n个不同的元素中任意挑选m(m<=n)个元素，所有的组合个数，就是从n个元素中挑选m个元素的所有组合数 $C_{n}^{m}$ 。

三、应用举例：

只懂概念，是肯定不行的。来！上题！巩固！

从4名男生、3名女生中，挑选3名代表，求：

至少有一名女生的不同选法共有多少种?
代表中男、女都要有的不同的选法多少种？

没算错吧！哈哈，思路可是这样的

要选取至少一名女生，不就是如下思路

直接法

1女2男
2女1男
3女0男

间接法

所有可能：0女3男

那有没有小可爱的思路是这样的呢？

哪为什么不能这样呢，即先选取1个女生，有3种可能，随后在剩下的6个人中，在选取2个人，这种思想错误吗，还是少判断哪里了？

这种思想是错误的，原因在于存在重复计数的情况。

按照你所说的思路，先从3名女生中选1名女生，有C31=3种选法；然后从剩下的6个人（4名男生和2名女生）中选2个人，有C62=2!(6−2)!6!=2×16×5=15种选法。根据分步乘法计数原理，这样得到的选法总数是3×15=45种。

下面举例说明重复计数的情况：

假设3名女生分别为A、B、C，4名男生分别为a、b、c、d。

情况一：先选女生A，然后从剩下6人中选B和a，得到组合{A,B,a}。

情况二：先选女生B，然后从剩下6人中选A和a，得到组合{B,A,a}。

这两种情况实际上是同一个组合{A,B,a}，但按照你的方法却被当作两种不同的选法进行了计数。

对于每一个包含2名女生的组合都会出现这样的重复情况，对于包含3名女生的组合，重复的情况会更复杂。所以这种先选1名女生再从剩下6人中选2人的方法不能正确计算至少有一名女生的选法数量。

OK啦，本题的正确答案是， $C_{3}^{1}\times C_{4}^{2}+C_{3}^{2} \times C_{4}^{1}+C_{3}^{3}=31$