快速入门深度学习系列(2)----损失函数、逻辑回归、向量化

已于 2025-05-08 20:51:09 修改
阅读量583 收藏 4
点赞数 14
分类专栏： 快速入门深度学习 文章标签： 深度学习 神经网络 人工智能
于 2025-05-08 20:50:31 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2303_76162328/article/details/147799197
版权

针对深度学习入门新手目标不明确 知识体系杂乱的问题 拟开启快速入门深度学习系列文章的创作

旨在帮助大家快速的入门深度学习

写在前面：

本系列按照吴恩达系列课程顺序发布(说明一下为什么不直接看原笔记 因为内容太多 没有大量时间去阅读 所有作者需要一次梳理清楚 并整理思路 方便后续学习

对于入门的建议就是 在看文章的时候 如果有不懂的概念及时的搜索一下

本人学识有限 以上内容均根据本人理解 如有不对的地方大家多多指正 欢迎交流

本系列吴恩达深度学习入门系列作为起点 可能会穿插代码或者公式的推导

本系列也是对本人自2月25日以来学习深度学习内容的梳理与总结

希望我们都可以亲手杀死曾经那个颓废的自己！

---------------------------------------------------------------------------------------------------------------------------------

逻辑回归用于二分类任务 本文也以这个例子进行说明

如图 这是一个二分类任务 1代表猫 0代表狗

在计算机中 图像的表示形式如下图所示 这里有三个通道 红绿蓝 这里只是化了5*4个格子 代表像素 实际上 像素可以是64*64 或者更大

以64*64像素为例 在输入之前 我们要把这些像素用特征向量来表示 对于本例 像素的大小就是64*64*3 

这里的维度 大家一定搞清楚 很重要 不理解的看下面的图

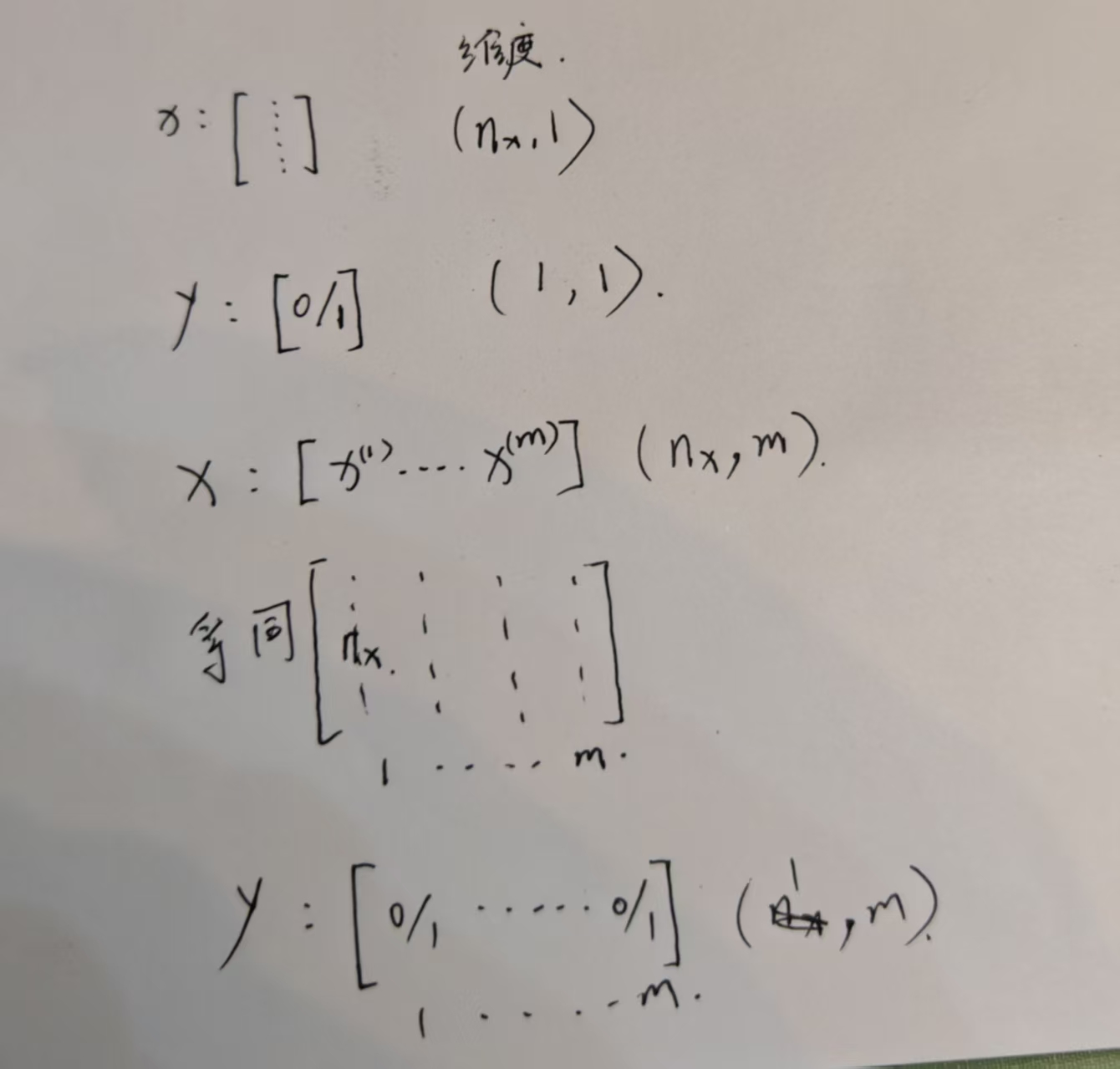
解释一下这张图 首先y预测就是对y的估计 表示了y=1是一只猫的可能性 我们需要用w x b表示y预测 但是这样是不行的 因为我们输出的是概率 在0-1之间 所以要套上一层sigmoid激活函数

对于激活函数的定义 和曲线已经画出 顺便说一下 训练的过程就是不断学习w b的过程 以更好的预测y

损失函数

我们定义一个损失函数 通过让损失函数更趋近于0来更新w b 来更加靠近真实的y

本例损失函数如下图 已经解释的很清楚了

代价函数

注意在表示第i个样本时 括号在上面

梯度下降法

可以看出 梯度下降就是在不断寻找J最小的点 并以此确定w b

计算图

逻辑回归中的梯度下降

对于M个样本的逻辑回归

下面写的有点乱 维度可以看这张 对于W的维度 还是有一些不确定 希望大佬指正

轻松入门自然语言处理系列 03 机器学习基础-逻辑回归
CUFEECR的博客
03-19 2238
本文主要介绍了机器学习的基础模型逻辑回归模型：逻辑回归中的条件概率，包括逻辑回归的应用、理解基准、分类问题、逻辑函数和样本条件概率；逻辑回归的目标函数，包括最大似然估计、逻辑回归的似然函数和逻辑回归的最大似然估计；梯度下降法，包括求解函数的最小值最大值、梯度下降、逻辑函数求导和逻辑回归的梯度下降法；随机梯度下降法，包括梯度下降法的缺点、随机梯度下降法、小批量梯度下降法、基于小批量梯度下降法实现逻辑回归；案例-预测银行客户是否会开设定期存款账户，包括问题描述、数据理解、数据预处理、模型训练、模型评估等。
深度学习知识点全面总结
热门推荐
专注大数据与人工智能技术分享，欢迎私信加群互相学习！
01-05 32万+
本文详细介绍深度学习概念及原理，参考网上相关资料汇总，内容包含众多章节，包括神经网络基础及常见深度学习网络结构介绍，用于个人学习总结，适合深度学习初学者学习。同时介绍机器学习常见的分类算法：SVM、神经网络、随机森林、逻辑回归、KNN、贝叶斯。常见的监督学习算法：感知机、SVM、人工神经网络、决策树、逻辑回归.........
Datawhale AI 夏令营：从baseline入门深度学习----Task 2
2302_80309108的博客
07-17 1581
ImageNet 包含超过1400万张注释过的图像，这些图像分布在超过2.2万个类别中。它的规模之大使得它成为深度学习模型训练和评估的理想数据集。ImageNet 数据集中的图像包含了各种场景、物体、背景和遮挡情况，这为算法提供了极大的挑战。这种多样性使得在 ImageNet 上训练的模型能够学习到鲁棒的特征，从而在现实世界应用中表现良好。ImageNet 提供了一个标准的性能基准，研究者可以通过在 ImageNet 上的表现来比较不同模型的性能。
深度学习-2.3损失函数
weixin_43186779的博客
03-07 1122
在之前的文章中，已经建立了最基础的深层神经网络，并能够理解网络的正向传播过程，接下来，我将分享深度学习网络的学习和训练过程，并从最小二乘和梯度下降算法开始拓展，介绍神经网络的损失函数、常用优化算法等信息，实现神经网络的学习和迭代。
深度学习原理-----线性回归+梯度下降法
didiaopao的博客
08-31 9096
本文主要从基础的角度讲解线性回归算法和梯度下降算法，力求用通俗的语言和简单的例子进行算法的讲解。
深度学习入门笔记（四）：向量化
种树最好的时间是10年前，其次是现在！！！
09-18 8663
声明 1）该文章整理自网上的大牛和机器学习专家无私奉献的资料，具体引用的资料请看参考文献。 2）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除。 3）博主才疏学浅，文中如有不当之处，请各位指出，共同进步，谢谢。 4）此属于第一版本，若有错误，还需继续修正与增删。还望大家多多指点。大家都共享一点点，一起为祖国科研的推进添...
深度学习-线性回归
2301_80249773的博客
09-24 1142
矢量化加速，正态分布（高斯分布）
深度学习06-pytorch从入门到精通
liaomin416100569的专栏
07-06 8176
构建5*3数组,只是分配了空间未初始化#这里产生个0-1之间的tensor张量，并且初始化print(x1)自己创建的数据集没有做任何维度的转换。for input,label in dsLoader: #四条数据分成了2批，循环两次。
计算机视觉深度学习入门笔记-从理论到实战案例
qq_60818566的博客
08-25 1384
深度学习是一种机器学习的分支，致力于模拟人脑神经网络的工作原理。通过构建具有多层次结构的神经网络模型，深度学习可以从大量数据中学习和提取特征，以解决各种复杂的任务。在过去的几年中，AI在各个领域都有突飞猛进的发展。就如同追求物理学中大统一，对于各式的AI模型，人们希望建立一个统一的通用人工智能（AGI）。在自然语言模型中，ChatGPT或许已经具有在部分领域AGI的雏形，尽管其仍然存在很多问题，对于某些交互存在胡言乱语的情况。但不可否认的是，我们或许能够在有生之年见证真正的AGI的诞生。
深度学习入门---《白话机器学习的数学》笔记
lyz1_2_3的博客
11-22 1716
参考《白话机器学习的数学》，相关学习笔记分享
Matlab系列--MATLAB快速入门机器学习和深度学习，傻瓜式图像分类学习项目，.zip
02-24
结合提供的"Matlab系列--MATLAB快速入门机器学习和深度学习，傻瓜式图像分类学习项目"资料，你将能够快速上手并逐步提升自己的技术水平。在实践中不断迭代和优化，你会发现MATLAB是一个强大且灵活的平台，能助你在...
逻辑回归中的损失函数：交叉熵损失详解与推导
AI天才研究院
05-03 746
逻辑回归（Logistic Regression）是机器学习中最基础的分类算法之一，广泛应用于二分类和多分类问题。其核心优势在于模型简单、可解释性强，且损失函数设计与概率理论深度契合。本文聚焦逻辑回归的核心组件——交叉熵损失函数交叉熵损失为何能有效衡量分类模型的预测误差？二分类与多分类场景下的损失函数形式有何联系与区别？如何通过极大似然估计推导出交叉熵损失的数学表达式？工程实践中如何高效实现交叉熵损失的计算与梯度求解？从信息论基础引入熵、KL散度、交叉熵的核心概念。
Pycharm（十九）深度学习
higerwy的博客
05-06 1336
深度学习是机器学习中的一种特殊方法，它使用称为神经网络的复杂结构，特别是“深层”的神经网络，来学习和做出预测。深度学习特别适合处理大规模和高维度的数据，如图像、声音和文本。深度学习、机器学习和人工智能之间的关系如下图所示：深度学习⊆机器学习⊆人工智能优点：1）精度高，性能优于其他的机器学习算法，甚至在某些领域超过了人类；2）随之计算机硬件的发展，可以近似任意的非线性函数；3）近年来在学界和业界受到了热捧，有大量的框架和库可供调。缺点：1）黑箱。
【深度学习|学习笔记】 梯度提升机（Gradient Boosting Machines, GBM）模型详解，附代码。
2401_89898861的博客
05-10 1146
【深度学习|学习笔记】 梯度提升机（Gradient Boosting Machines, GBM）模型详解，附代码。
Python数据分析案例74——基于内容的深度学习推荐系统（电影推荐）
weixin_46277779的博客
05-10 1370
电影数据集构建推荐系统，结合内容推荐和深度学习两种方法。预处理、探索性分析，加权平均法和余弦相似度进行基于内容的推荐，计算电影的相似度并生成推荐结果。并且使用深度学习模型，构建评分预测和检索任务，用户个性化推荐和评分预测。
CNN处理图片
minato_wdz的博客
05-09 938
iltera​rgnp..array([[1/162/16erfiltera​rg−1)==[3120。
深度学习 自然语言处理(RNN) day_02
最新发布
qq_59348412的博客
05-13 850
感知机由于结构简单，完成的功能十分有限。可以将若干个感知机连在一起，形成 一个级联网络结构，这个结构称为“多层前馈神经网络”（Multi-layer Feedforward Neural Networks）。所谓“前馈”是指将前一层的输出作为后一 层的输入的逻辑结构。每一层神经元仅与下一层的神经元全连接。但在同一层之内， 神经元彼此不连接，而且跨层之间的神经元，彼此也不相连。循环神经网络（Recurrent Neural Network，RNN）是一种神经网络结构，专门用于处理序列数据。
PyTorch实战（4）——卷积神经网络(Convolutional Neural Network, CNN)详解
盼小辉丶的博客
05-12 1174
卷积神经网络 (Convolutional Neural Network, CNN) 是一种广泛应用的深度学习模型。通过参数共享、局部感知和空间结构等优势，能够更好地处理图像数据，并在图像识别、目标检测和图像生成等任务中展现出强大的能力。在本节中，介绍了卷积的计算方法以及卷积神经网络的基本组件，并使用 PyTorch 构建了卷积神经网络以深入了解其工作原理。
The Deep Learning Compiler: A Comprehensive Survey (深度学习编译器：全面调查)
m0_58988991的博客
05-13 643
《深度学习编译器：全面调查》一文由Mingzhen Li等人撰写，发表于2021年3月1日的《IEEE Transactions on Parallel and Distributed Systems》。该文章系统性地回顾了深度学习编译器的发展现状，探讨了其在优化深度学习模型部署和性能提升中的关键作用。文章详细分析了现有深度学习编译器的架构、优化技术及其在不同硬件平台上的应用，并指出了当前面临的挑战和未来的研究方向。这项调查为研究人员和开发者提供了宝贵的参考，有助于推动深度学习编译器技术的进一步发展。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值