概率论与数理统计（随机事件与概率）

1随机事件与概率

1.1随机事件及其运算规律

1.1.1运算

1. 交换律
2. 结合律
3. 分配律
4. 德摩根律

1.2概率的定义及其确定方法

1.2.1概率的统计定义

频率 设在 n 次试验中，事件 A 发生了(A)次，则称为事件 A 发生的频率。

1.2.2概率的统计定义

在一组恒定不变的条件下，将某试验重复进 行n次，随着n 增大，事件A发生的频率，总 在某一固定常数p 左右摆动，我们称这个稳定值 p 为事件A的概率, 记作 P(A). f (A)

性质：

非负性：

规范性：

可列可加性：

1.2.3确定概率的古典方法

条件：

• 试验的样本空间只包含有限个元素
• 试验中每个基本事件发生的可能性相同

古典概率的确定：

设试验 E 的样本空间由n 个样本点构成， A 为 E 的任意一个事件，且包含 m 个样本点，则事 件 A 出现的概率记为:

常用计数方法：

1.2.3.1重复组合

从 n 个不同元素中每次取出一个， 放回后再取下一个，如此连续取r次所得的组合 称为重复组合，此种重复组合数共有：

1.2.3.2不全相异元素的排列

在n个元素中，有m类不同元素、每类各有k1 , k2 ,… km 个，将这n个元素作全排列，共有如下种方式：

或：

1.2.3.3环排列

从n个不同元素中，选出m个不同的元素排成一 个圆圈的排列，共有：

1.2.4古典概型基本模型

1.2.4.1无放回地摸球

设袋中有4 只白球和 2只黑球, 现从袋中无 放回地依次摸出2只球,求这2只球都是白球的概率

解答较简单。

1.2.4.2有放回地摸球

设袋中有4只红球和6只黑球,现从袋中有放 回地摸球3次,求前2次摸到黑球、第3次摸到红球 的概率.

基本事件总数为,A 所包含基本事件的个数为:

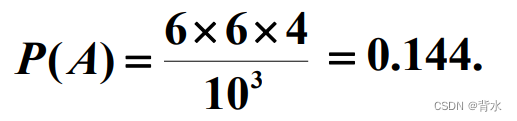
1.2.4.3分球入盒模型(盒子容量无限)

把 4 个球放到 3个盒子中去,求第1、2个 盒子中各有两个球的概