2024年本科生数学建模C题国奖Latex版本

所需的图片

源码（可运行）：

\documentclass[12pt]{ctexart} 
\usepackage{array}
\usepackage{geometry}  
\usepackage{graphicx}  
\usepackage{amsmath, amssymb}  
\usepackage{booktabs}  
\usepackage{enumerate} 
\usepackage{verbatim}
\usepackage{url}
\usepackage{fancyhdr}

\pagestyle{fancy}  % 使用 fancy 页眉页脚样式
\fancyhf{}  % 清空默认的页眉页脚
\fancyfoot[C]{\thepage}  % 在底部中央显示页码
\renewcommand{\headrulewidth}{0pt}  % 去掉页眉的横线
%\pagestyle{empty}  % 去掉页眉和页脚的页码
% 页面设置  
\geometry{a4paper, margin=2.5cm}  
\setlength{\parindent}{2em} % 2em 相当于两个字符的宽度

%\title{基于收益最大化的种植策略探究}  
%\author{张文瑞、陈名湛、王晨屹}  
%\date{\today}  

\begin{document}  
%    \maketitle  
    
    % 摘要页  
    %\newpage 
    \section*{基于收益最大化的种植策略研究} 
    %\title{基于收益最大化的种植策略探究}
    \begin{center}  
        \Large\textbf{摘要}  
    \end{center}  
    
    \noindent   
    
    
    随着乡村振兴战略的实施，使农作物收益最大化具有重要意义。同时随着市场需求的改变，农产品销售面临诸多潜在风险。本文从如何使农产品收益最大化出发，根据需求变化灵活选取不同的约束条件和求解算法，设计不同的农作物种植结构，以达到充分利用耕地资源的目的。
    
    
    针对问题一，我们首先对不同作物亩产收益进行分析，发现种植豆类的收益低于种植蔬菜与粮食，因此我们提出了种植豆类收益低的假设。在此假设基础上，本文建立\textbf{单目标多约束优化模型}，以农作物种植收益作为目标函数，考虑到题目中的约束函数多为非线性约束，因此常规的线性规划算法不容易实现，因此我们基于\textbf{遗传算法}的相关思想，针对种植策略的有效性和高收益性进行全局优化，通过反复迭代得到了在该题约束下最优的种植策略。
    
    
    针对问题二，由于诸多变量发生波动，若继续设计常规的单目标规划模型容易造成较大误差。因此本文采用\textbf{概率规划模型}，利用经济学中的\textbf{几何布朗运动模型}将价格随时间变化的随机过程转化为微分方程形式，再利用\textbf{对数收益的正态分布模型}模拟价格的变化，使其在一定取值范围内满足正态分布，接着通过重复模拟收益生成路径得到了农作物在不同年份收益的期望值分布列。考虑到潜在的种植风险，本文引入了\textbf{在险价值}来模拟可能出现的最大损失。最后，考虑到不确定因素下集合的选取问题可能会对优化过程产生较大影响，本文采用了\textbf{鲁棒优化模型}，并重新设计了目标函数与约束条件，进而得出了本题的最佳优化种植结构：单季地以种植红薯为主。水浇地奇数年第一季主要种植茄子和豇豆，第二季全部种植水稻，偶数年第一季全部种植茄子，第二季种植水稻。
    
    
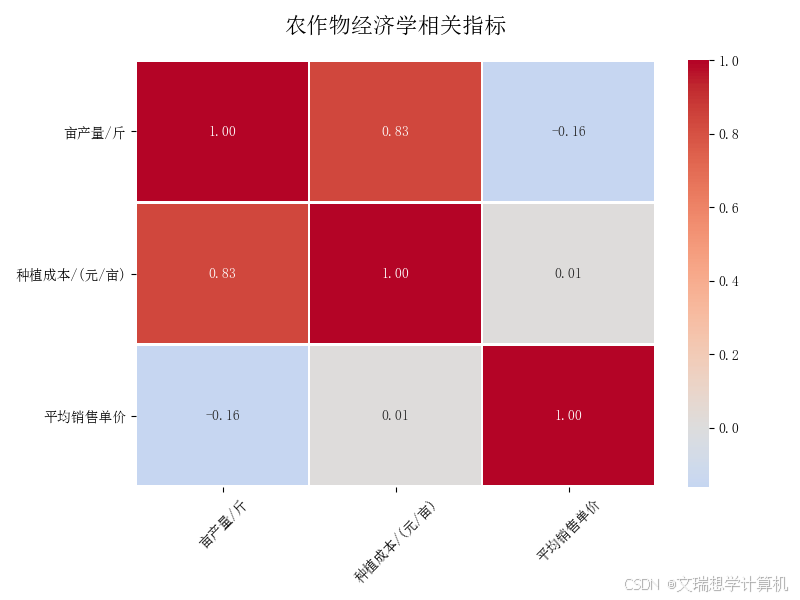
    针对问题三，本文计算\textbf{speraman相关系数}分析各作物预期销售量，种植成本，销售价格之间的关系，结果表明亩产量与种植成本之间具有较强的正相关性，平均销售单价与种植成本之间存在弱关联性。此外，平均销售单价与亩产量之间则展现出一种微弱的负相关性。接着，我们引入\textbf{交叉弹性}来量化农作物之间的可替代性和互补性，并建立\textbf{交叉弹性矩阵}获得有关交叉弹性的约束条件，最后在\textbf{聚类分析算法}基础上增加交叉弹性约束，最后得出在亩产量-种植成本上存在部分呈现较强正相关性的农作物，在必要情况下这几种作物可以实现互相替代。并得出了新的种植结构：单季地奇数年保持不变，偶数年以荞麦为主要经济作物
    水浇地奇数年第一季主要种植茄子与豇豆, 第二季种植水稻；偶数年水稻茄子双季种植。普通大棚主要种植豇豆,辅种刀豆。智慧大棚单季则以茄子为主要粮食作物，其余粮食作物主要则种植土豆与西红柿, 双季主要种植豇豆，辅种刀豆。 
    
    
    
    
    
    
    
    \vspace{0.5cm}  
    \noindent \textbf{关键词：}  农作物结构调整，单目标多约束优化，概率规划模型，聚类分析
    \newpage
    
    % 正文部分  
    \section{问题重述}  
    \subsection{问题背景}  
    华北山区乡村的耕地资源有限，因此优化种植策略对于提高生产效益和降低风险至关重要。不同的土地条件下，选择合适的种植方式以使收益最大化是本文的主要研究目标。  
    
    \subsection{题目信息}  
    \begin{enumerate}  
        \item 露天耕地主要种植一季粮食，水浇地可种植一季水稻或两季蔬菜；大棚中，普通大棚适合种植一季蔬菜和一季食用菌，智慧大棚则适合种植两季蔬菜。地块和大棚每季可合种不同作物。  
        \item 每种作物在同一地块（含大棚）不能连续重茬种植。  
        \item 每块地三年内至少种植一次豆类作物。  
        \item 每种作物种植面积不宜太小。  
    \end{enumerate}  
    
    \subsection{待求解问题}  
    \begin{enumerate}  
        \item 在农作物未来的预期销售量、种植成本、亩产量和销售价格与2023年保持相对稳定的情况下，分别在两种超出预期销量的策略下给出该乡村2024到2030年农作物的最优种植方案。  
        \item 在农作物预期销售量、亩产量、种植成本与销售价格发生改变的情况下，综合考虑潜在的种植风险，给出该乡村2024到2030年农作物的最优种植方案。  
        \item 在问题二的基础上，分析各种农作物之间的关系和几种经济指标之间的相关性，给出该乡村2024到2030年农作物的最优种植方案，并与问题二中的方案进行对比分析。  
    \end{enumerate}  
    \newpage
    \section{问题分析}  
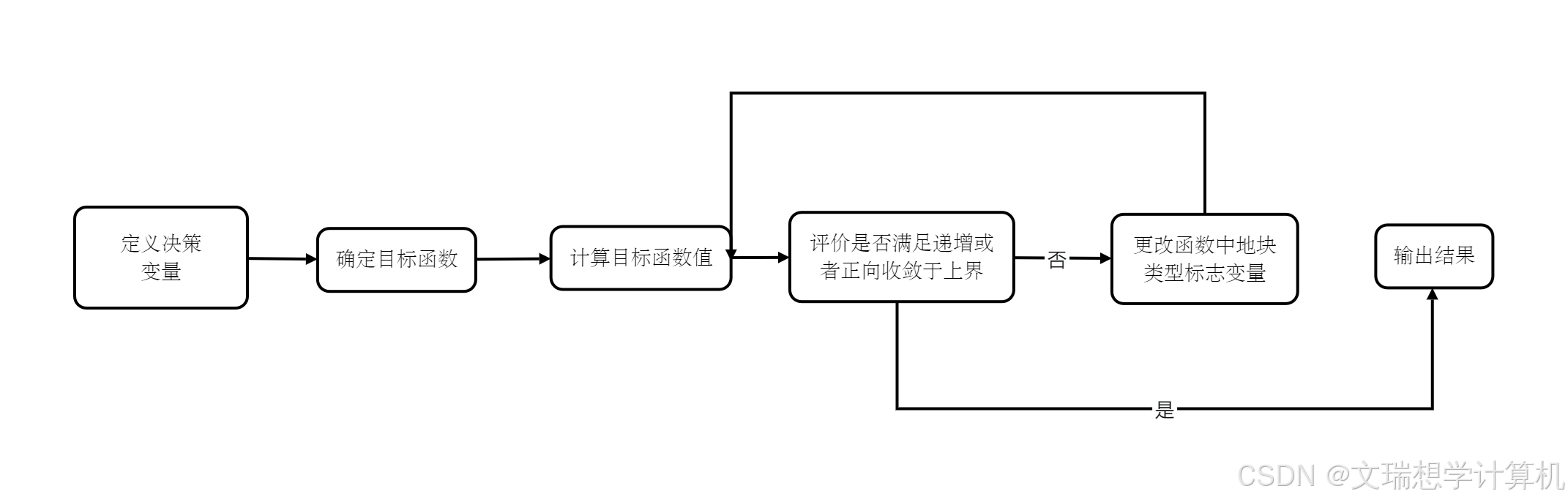
    \subsection{问题一的分析}  
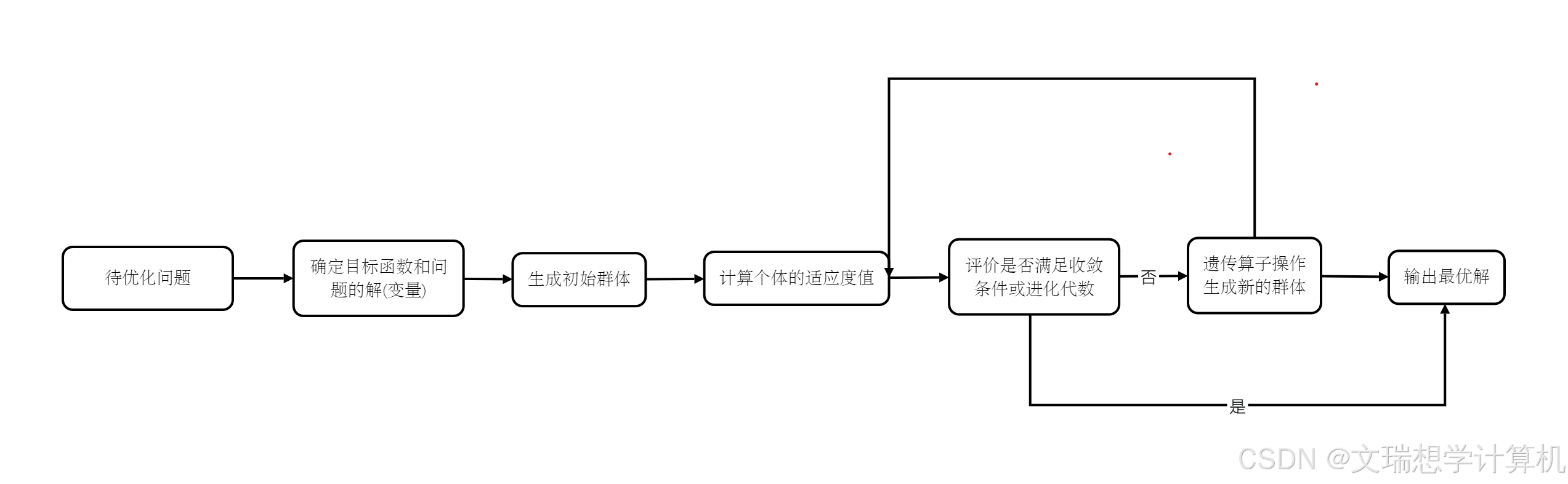
    该问题是一个带有多重约束条件的优化问题，目标是在满足约束条件的同时最大化农作物收益。由于约束条件复杂且非线性，我们采用现代优化算法进行求解。具体地，我们借助遗传算法的思想，产生一个可行的初始方案，并通过改变其部分结构来寻找其他更优解。通过锦标赛选择方法筛选后代，不断进行迭代，直到找出全局最优解。  
    
    \subsection{问题二的分析}  
    问题二中，农作物的各项经济指标会随时间发生波动。因此，我们引入了概率分布模型来模拟未来几年间各作物的销量、产量、成本及价格波动。对于变量的波动，我们采用经济学中的几何布朗运动（GBM）模型和对数收益的正态分布模型进行求解，得到农作物不同年份的价格、销量、成本与波动变量对应的期望值分布和在险价值。考虑到种植方案的连续性需求，结合本题不稳定性因素较多，需要稳健预测的特点，我们采用鲁棒优化算法求解最优种植方案。
    
    \subsection{问题三的分析}  
    在问题二的基础上，我们进一步分析各种农作物之间的关系和几种条件之间的相关性。首先，我们对第二问得到的预期销售量、销售价格和种植成本进行斯皮尔曼相关性分析，得到变量之间的斯皮尔曼相关性系数。其次，我们引入交叉弹性来量化农作物之间的可替代性和互补性，并建立交叉弹性矩阵获得交叉弹性约束条件。最后，在聚类分析基础上增加交叉弹性约束，得到最优种植方案。  
    
    @article{
\section{模型假设}  
\label{sec:assumptions}  
\begin{enumerate}[(1)]  
    \item 种植豆类作物的收益远低于其他作物的收益。
    \item 预测变量在波动范围内取值服从正态分布。
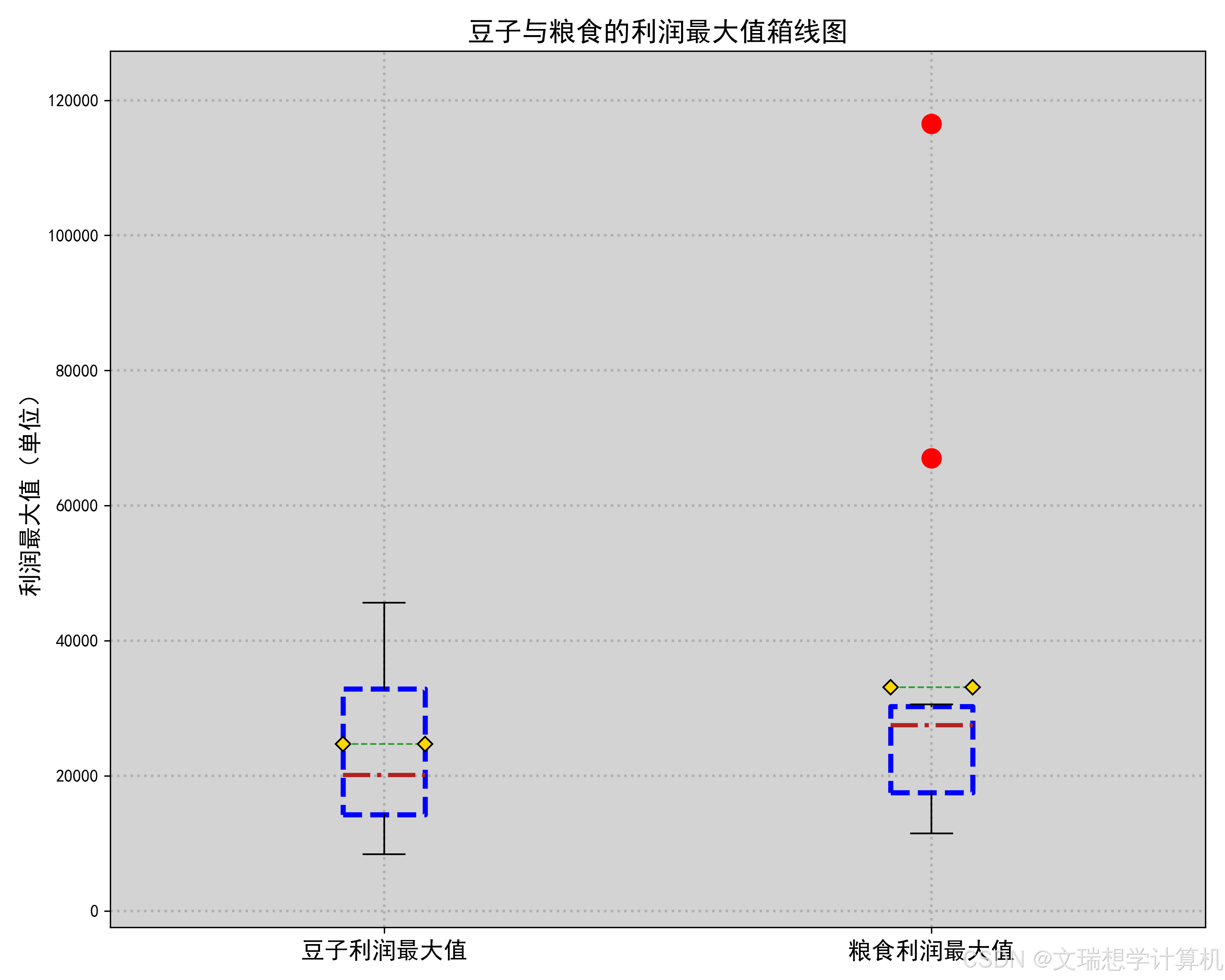
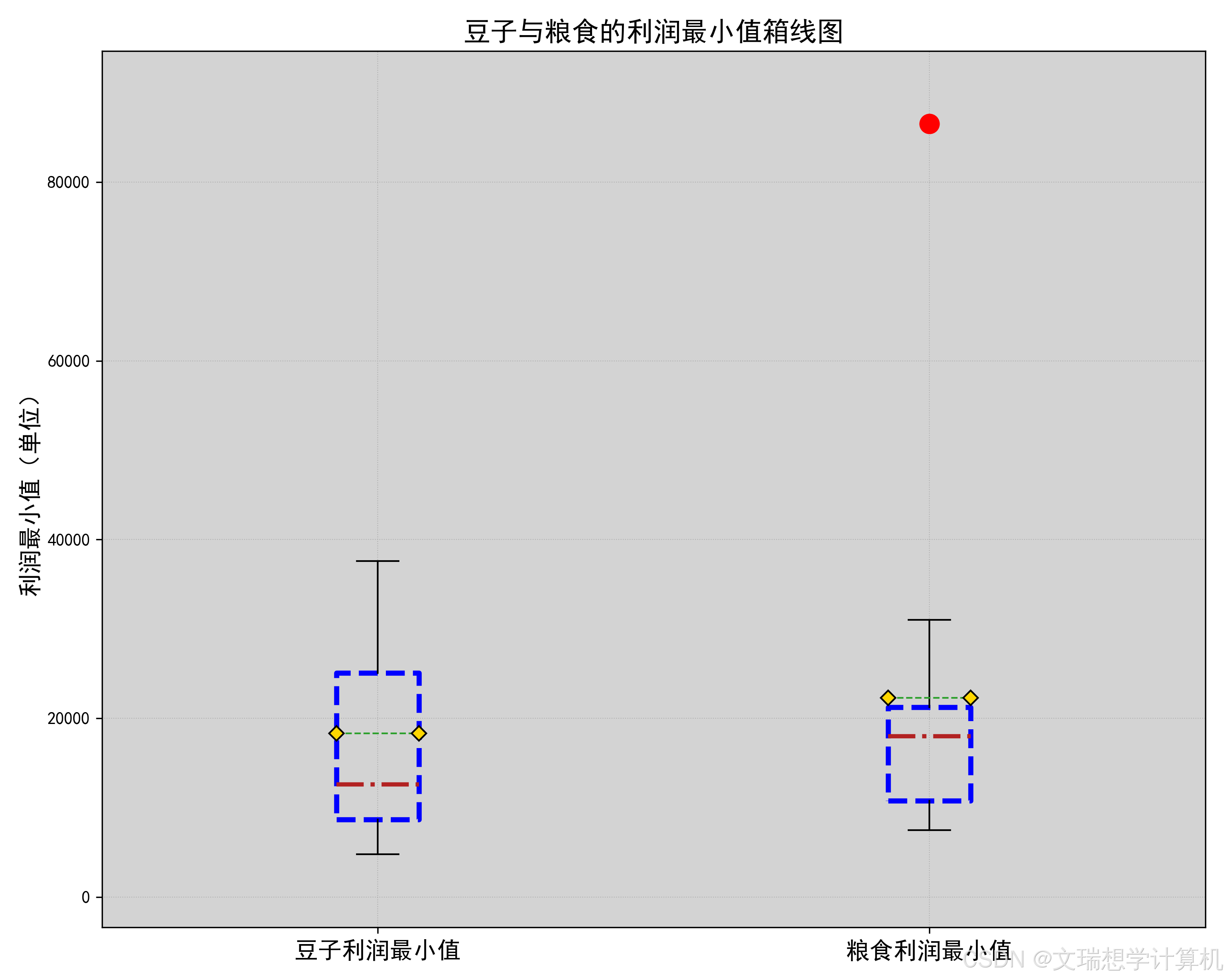
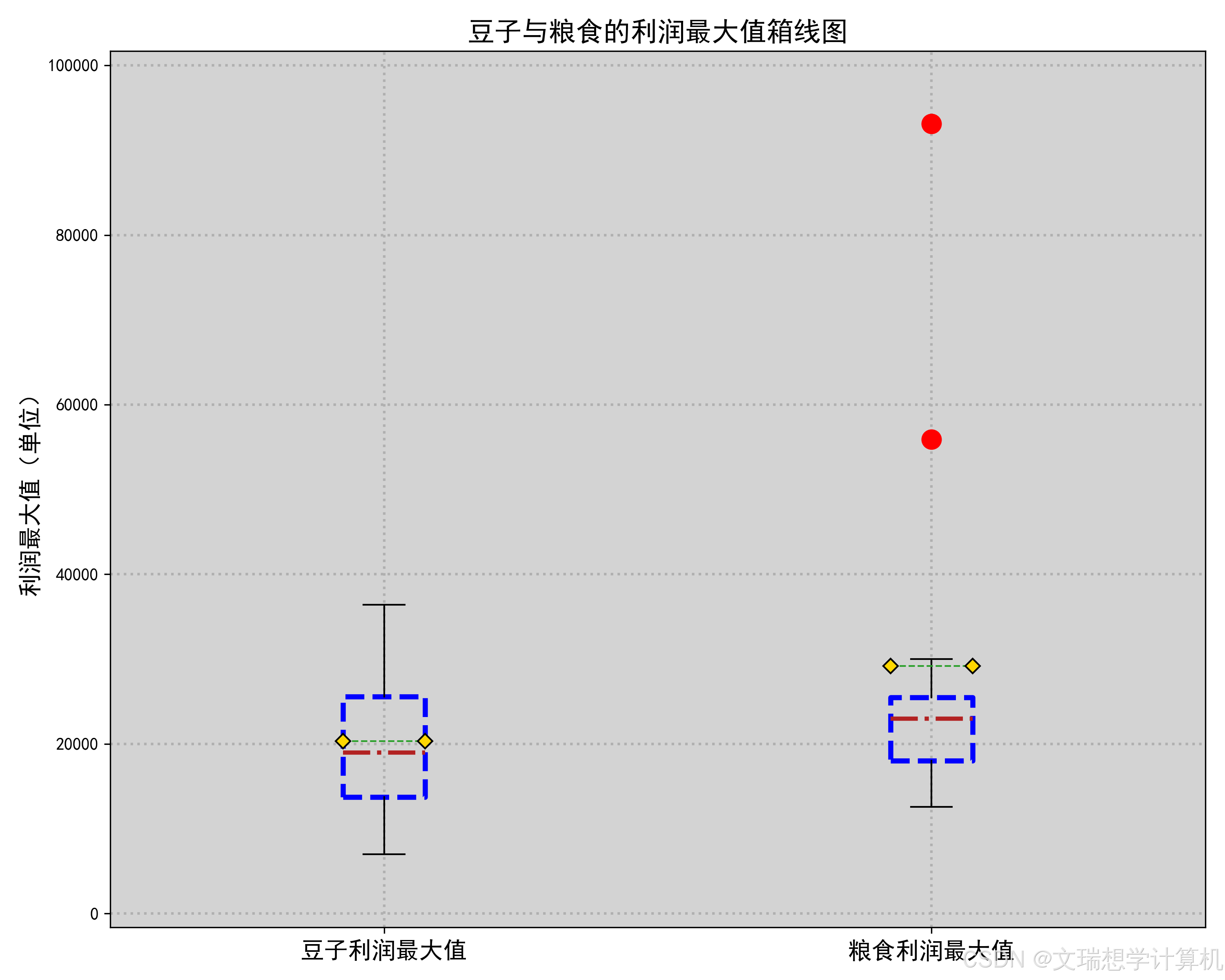
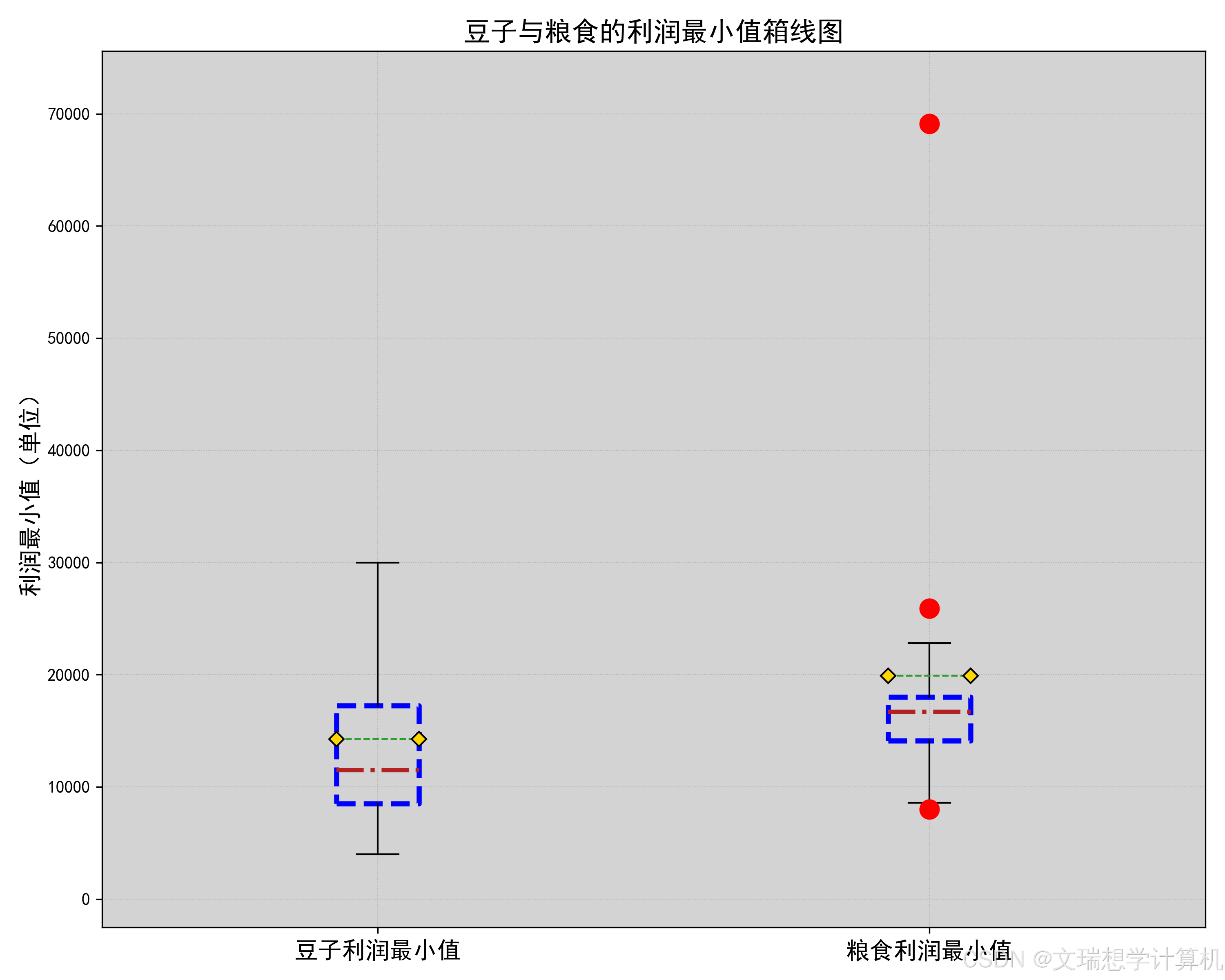
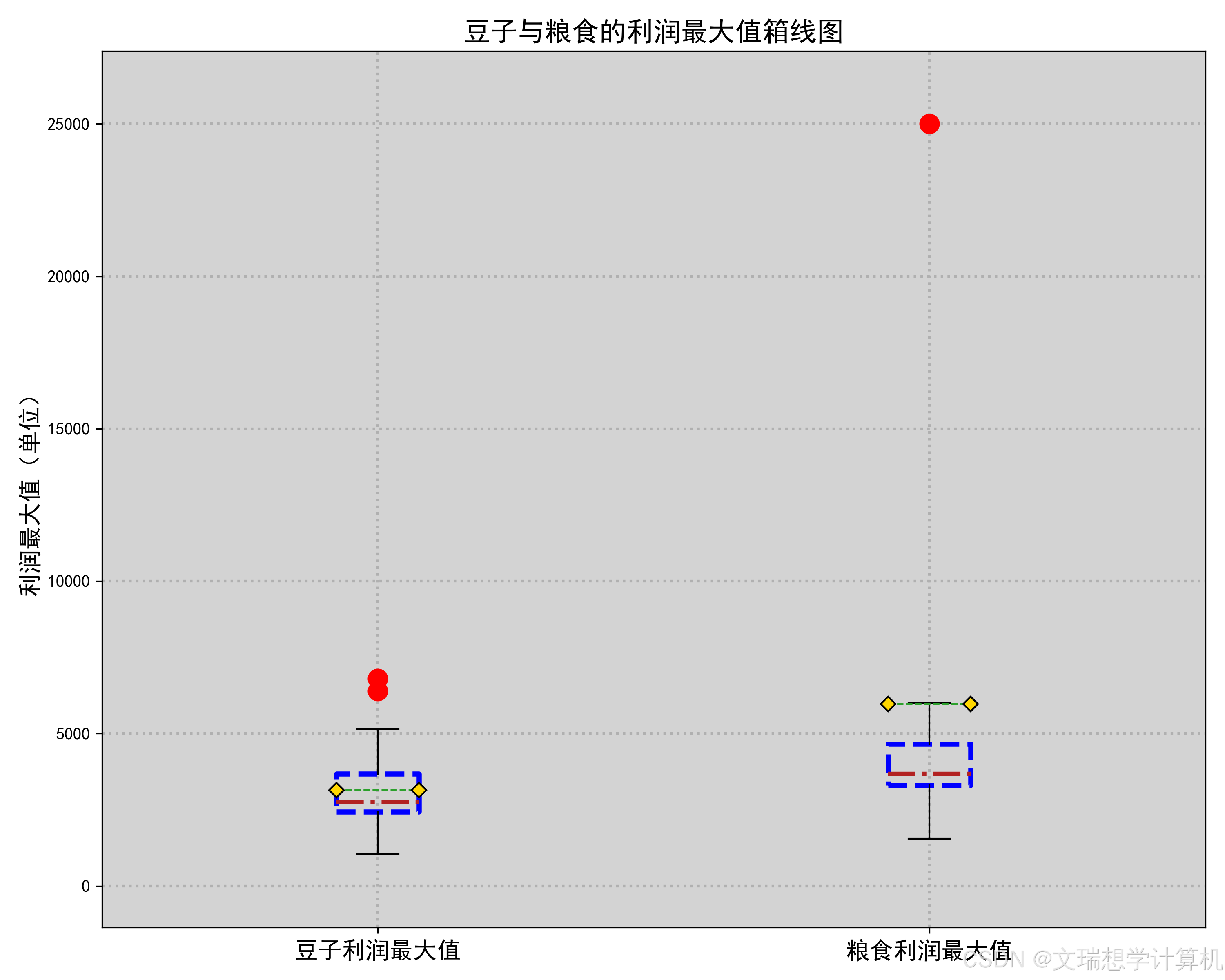
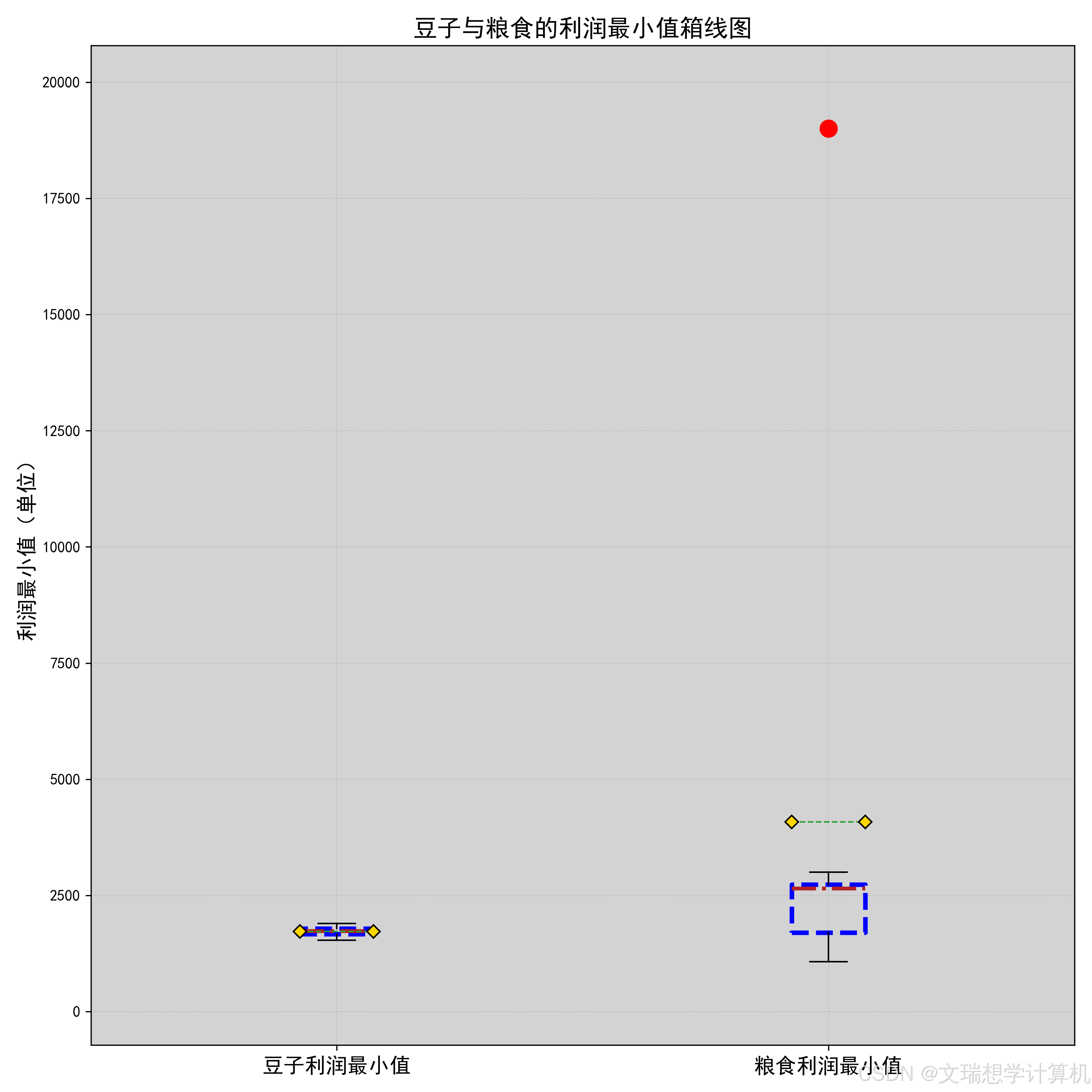
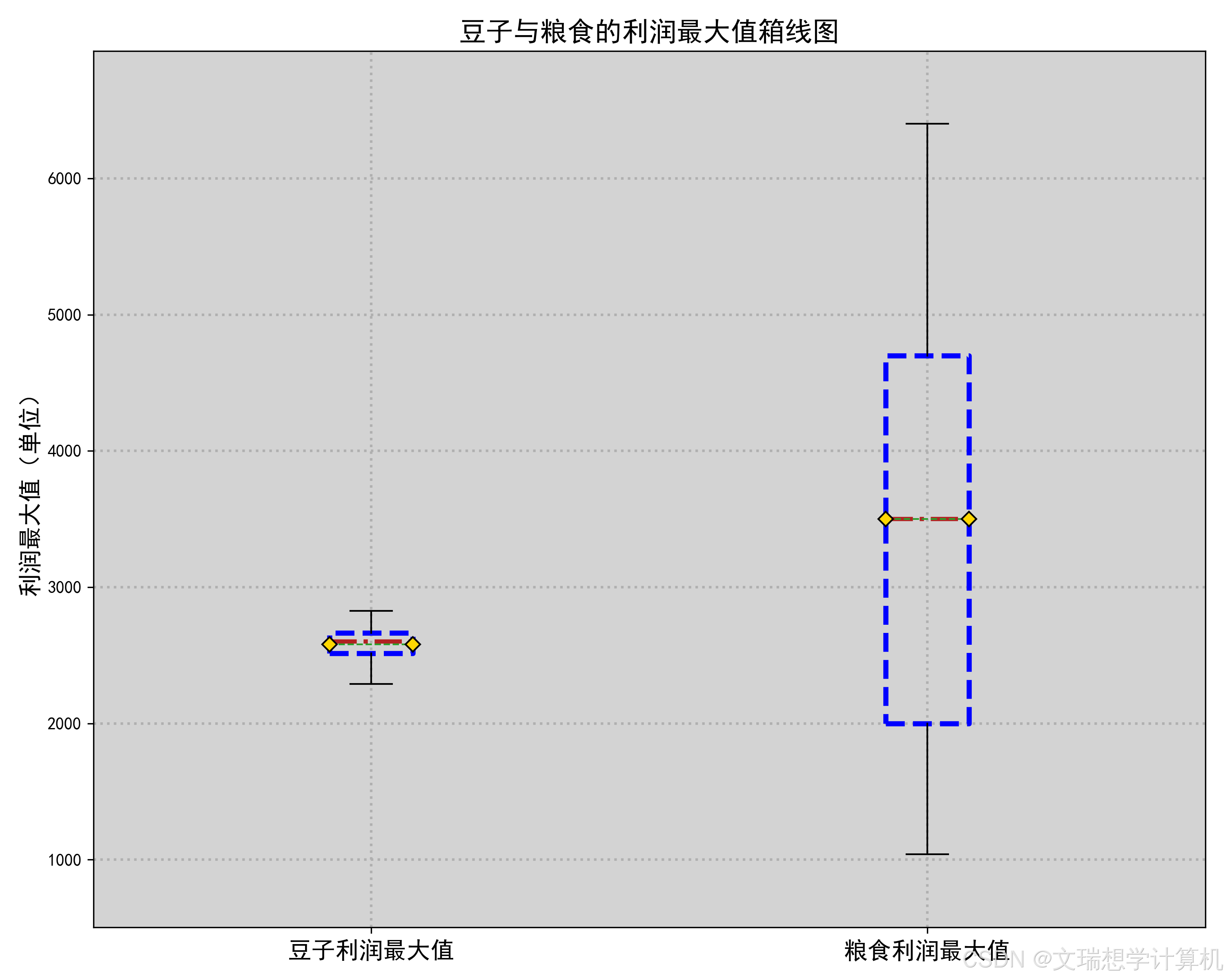
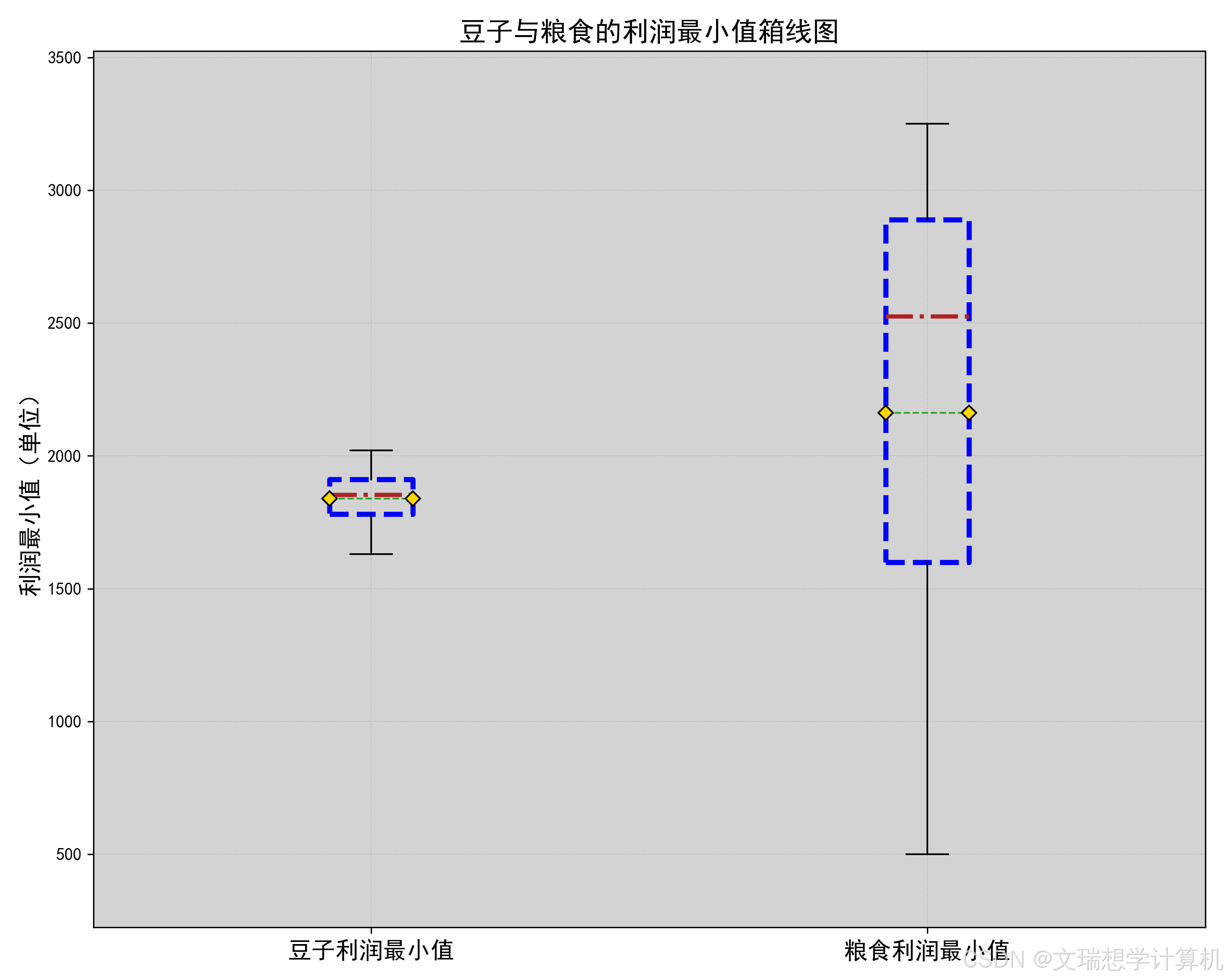
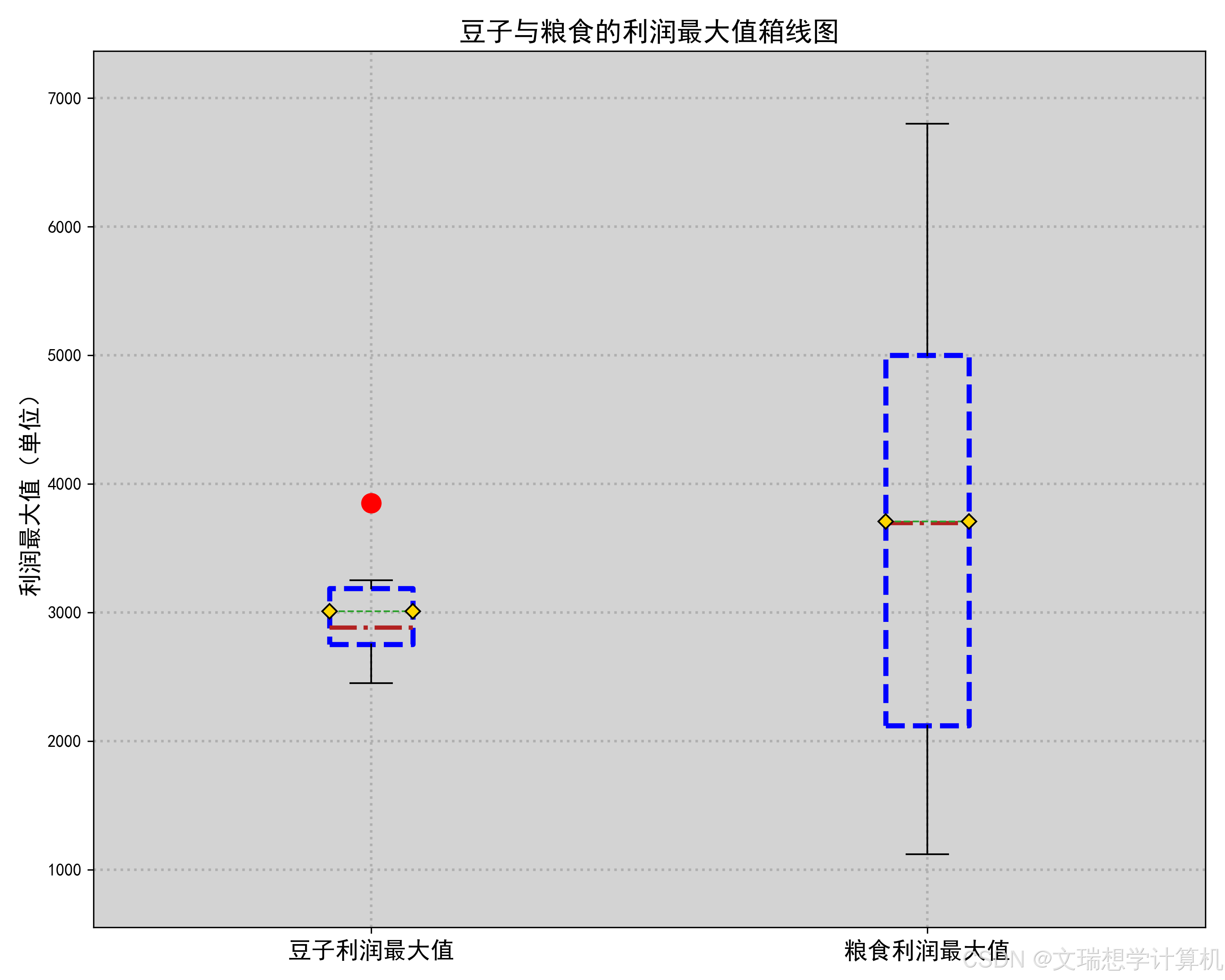
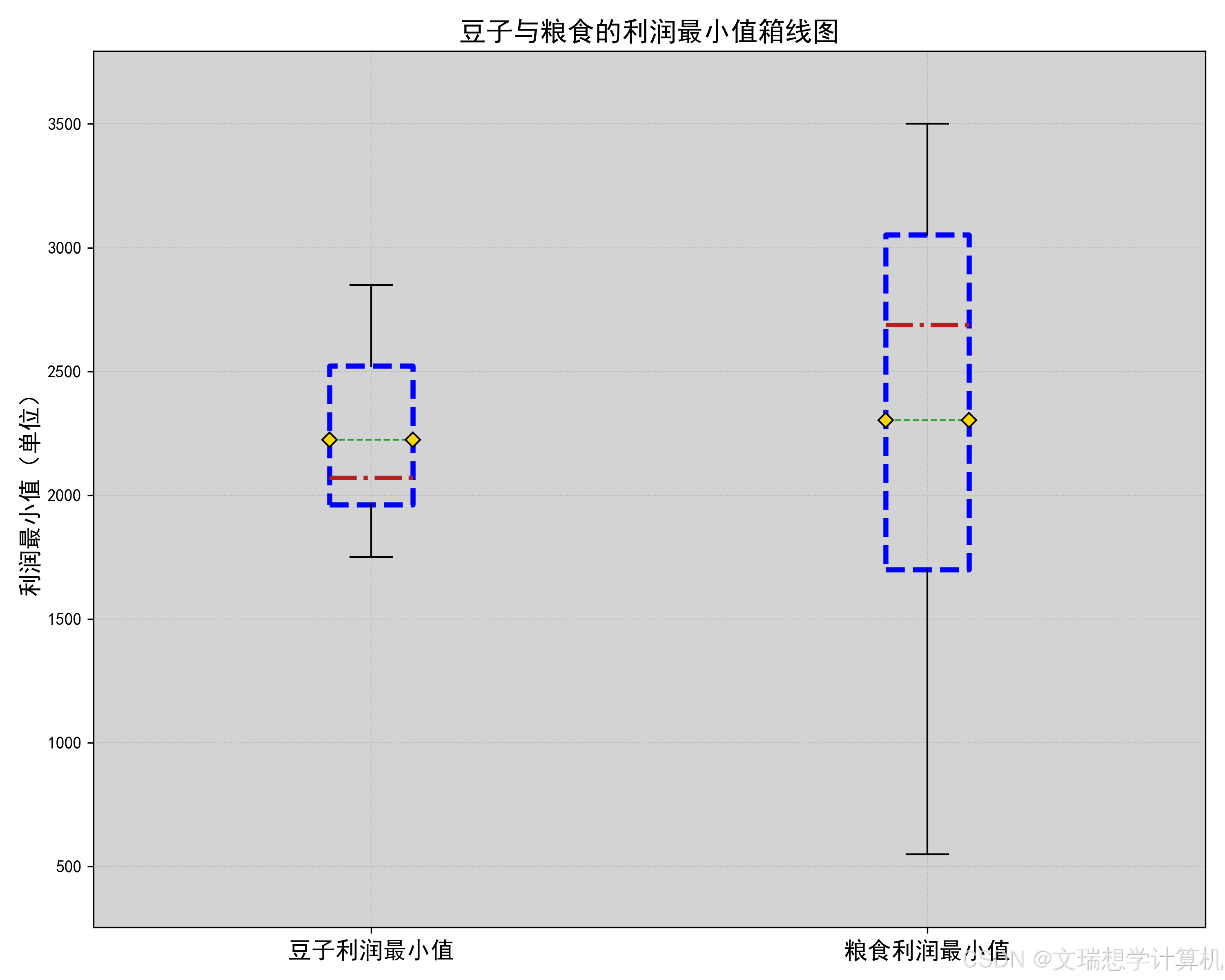
    \newline由于我们希望种植作物收益最大化，因此我们对于粮食，蔬菜与豆类的经济因素分别进行了考量。我们先计算出了每种作物的亩净产值，然后将作物分为豆类，粮食与蔬菜三类分别进行了比较，箱线图如下（部分放于附件）,
        author = {author},
        title = {title},
        journaltitle = {journaltitle},
        date = {date},
        OPTtranslator = {translator},
        OPTannotator = {annotator},
        OPTcommentator = {commentator},
        OPTsubtitle = {subtitle},
        OPTtitleaddon = {titleaddon},
        OPTeditor = {editor},
        OPTeditora = {editora},
        OPTeditorb = {editorb},
        OPTeditorc = {editorc},
        OPTjournalsubtitle = {journalsubtitle},
        OPTissuetitle = {issuetitle},
        OPTissuesubtitle = {issuesubtitle},
        OPTlanguage = {language},
        OPToriglanguage = {origlanguage},
        OPTseries = {series},
        OPTvolume = {volume},
        OPTnumber = {number},
        OPTeid = {eid},
        OPTissue = {issue},
        OPTmonth = {month},
        OPTpages = {pages},
        OPTversion = {version},
        OPTnote = {note},
        OPTissn = {issn},
        OPTaddendum = {addendum},
        OPTpubstate = {pubstate},
        OPTdoi = {doi},
        OPTeprint = {eprint},
        OPTeprintclass = {eprintclass},
        OPTeprinttype = {eprinttype},
        OPTurl = {url},
        OPTurldate = {urldate},
    }
    
    \begin{figure}[h]
        \centering
        \begin{minipage}{0.48\textwidth}
            \centering
            \includegraphics[width=\linewidth]{image7.png}
            \caption{豆类与粮食收益对比1}
            \label{fig:yield_comparison1}
        \end{minipage}\hfill
        \begin{minipage}{0.48\textwidth}
            \centering
            \includegraphics[width=\linewidth]{image8.png}
            \caption{豆类与粮食收益对比2}
            \label{fig:yield_comparison2}
        \end{minipage}
    \end{figure}
    
    
\begin{figure}[h]
    \centering
    \includegraphics[width=0.8\textwidth]{image13.png}  % 将宽度增加至 80% 的页面宽度
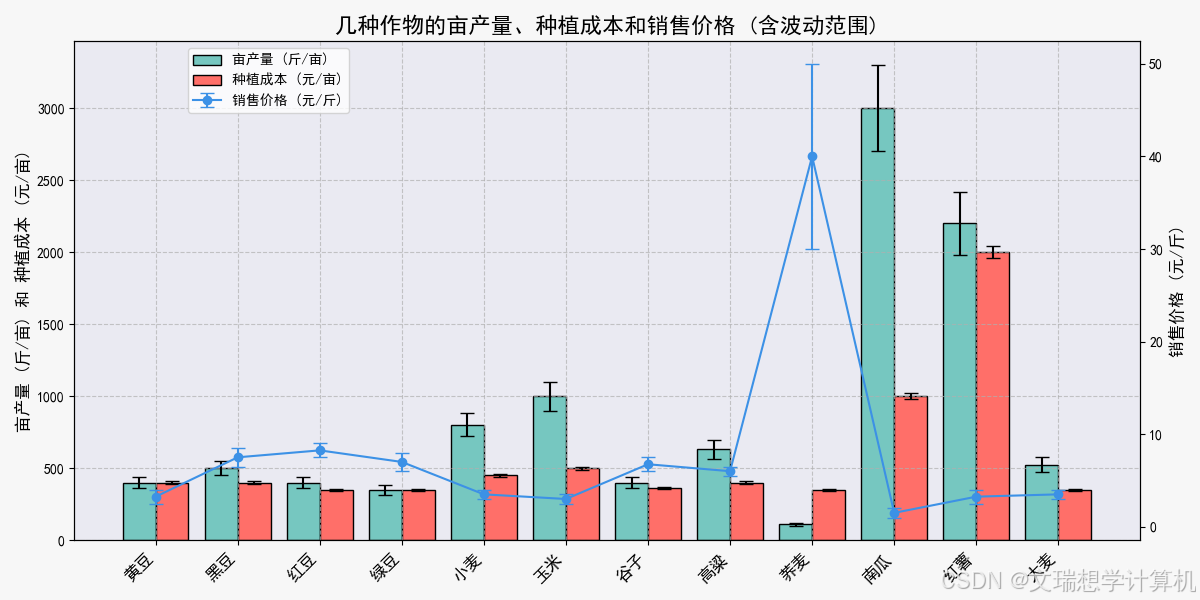
    \caption{作物指标}
    \label{fig:yield_comparison1}
\end{figure}

\begin{figure}[h]
    \centering
    \includegraphics[width=0.8\textwidth]{image14.png}  % 同样将第二张图片调整到 80%
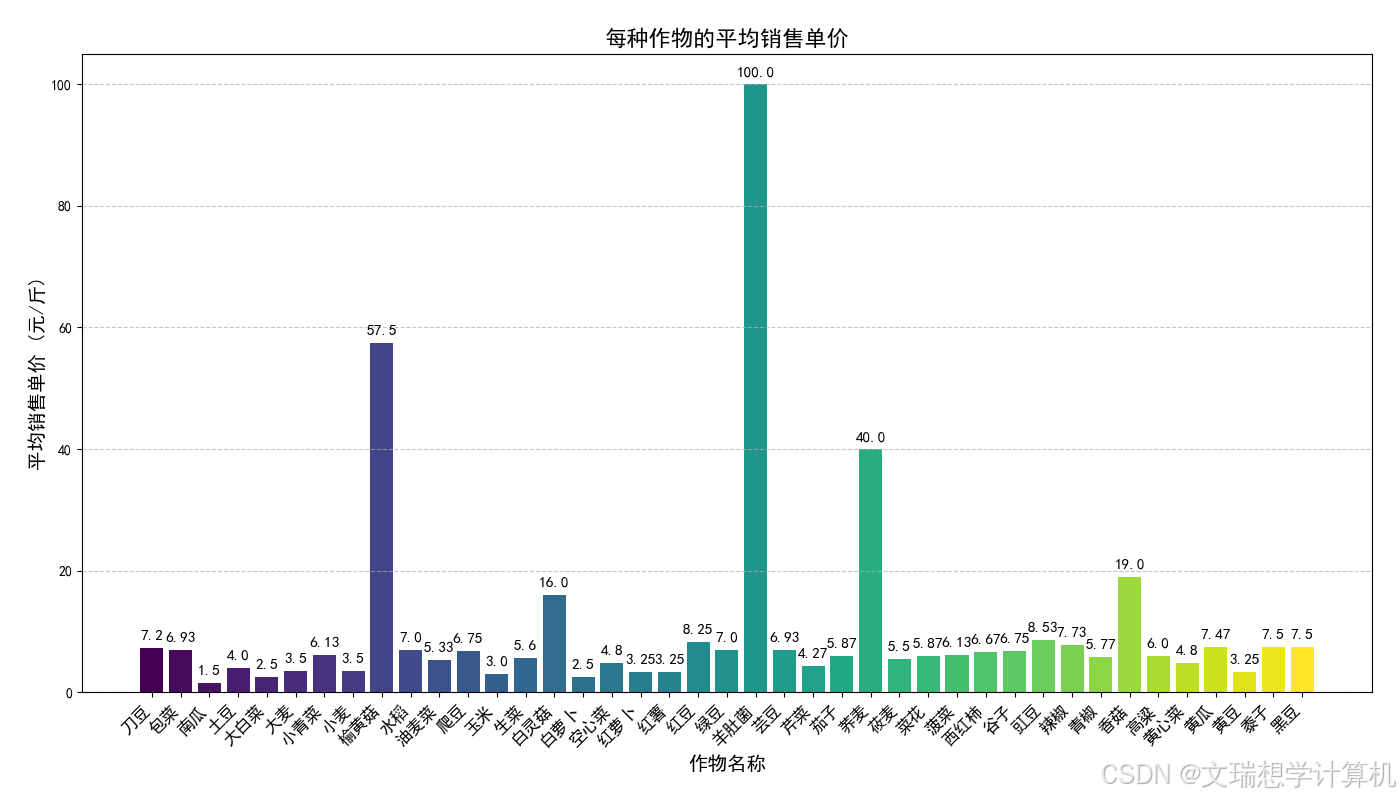
    \caption{作物平均销售单价}
    \label{fig:yield_comparison2}
\end{figure}

    通过箱线图我们可以很明显的看出种植豆类作物的收益均值与中位数均低于种植其他作物，因此假设成立，即应在满足题目约束条件的前提下尽可能少种植豆类作物.

    
    
    首先, 我们在题目给定的的作物售价范围内随机生成价格序列, 记作 \begin{equation*}\vec{y}=\left(y_1, y_2, y_3, \ldots, y_n\right)
    \end{equation*}
    
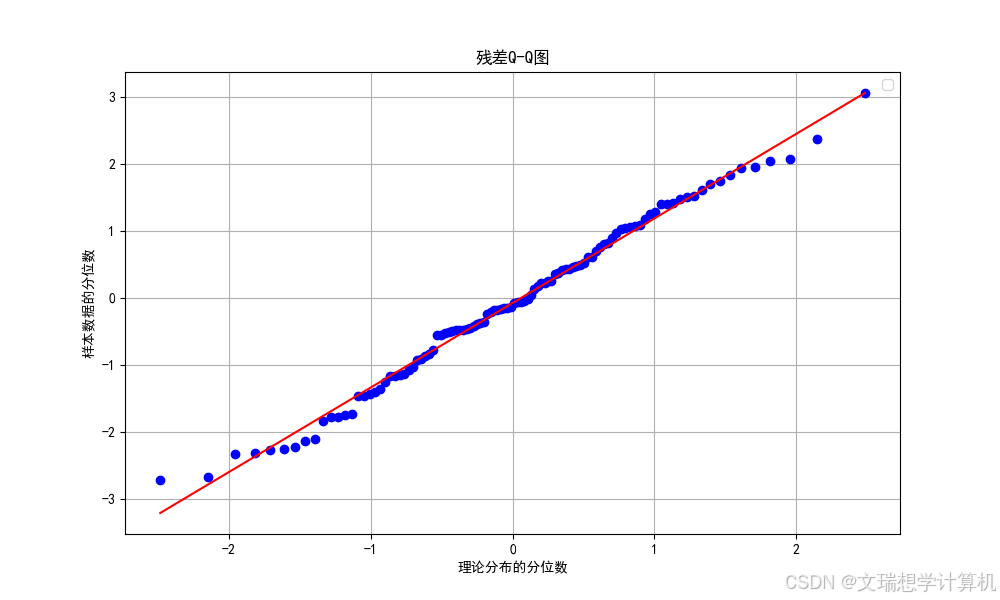
    其次, 我们使用对数收益正态分布模型生成同等数量的服从正态分布的随机价格序列, 记作 \begin{equation*}\vec{Y}=\left(Y_1, Y_2, Y_3, \ldots, Y_n\right)\end{equation*}, 计算得残差向量 $\vec{y}-\vec{Y}=\vec{e}=\left(e_1, e_2, e_3, \ldots, e_n\right)$ 。接下来本文进行残差的
    正态性检验并绘制残差 Q-Q 图:
    由图可知样本标准差与标准正态分布标准差比值为拟合直线的斜率, 得到的曲线越接近直线,说明越近似服从正态分布, 斜率越接近 1 说明越近似服从标准正态分布；拟合直线截距表示样本均值。
    对于拟合曲线的尾部行为有以下分析:
    若拟合曲线的尾部二阶导数大于零, 说明模拟变量具有正离群性, 存在比正态分布更多的极端值:
    
    \begin{equation}
    \frac{\sum_{i=1}^n 1 \cdot\left(\left|Y_i-\hat{\mu}\right|>3 \cdot \sigma\right)}{n}>\int_{\left|X_i-\hat{\mu}\right|>3 \cdot \sigma}^{\infty} \frac{1}{\sqrt{2 \cdot \pi \cdot \sigma^2}} \cdot e^{-\frac{(x-\mu)^2}{2 \cdot \sigma^2}} d x
    \end{equation}
    
    
    若拟合曲线的尾部二阶导数小于零, 说明模型变量具有负离群性, 样体中极端值小于正态分布的极端值:
    
    \begin{equation}
    \frac{\sum_{i=1}^n 1 \cdot\left(\left|Y_i-\hat{\mu}\right|>3 \cdot \sigma\right)}{n}<\int_{\left|X_i-\hat{\mu}\right|>3 \cdot \sigma}^{\infty} \frac{1}{\sqrt{2 \cdot \pi \cdot \sigma^2}} \cdot e^{-\frac{(x-\mu)^2}{2 \cdot \sigma^2}} d x
\end{equation}
    
    
    由本题的残差 $\mathrm{Q}-\mathrm{Q}$ 图可知，拟合曲线尾部特征呈现负离群值, 说明价格分布不仅服从正态分布, 并且离群值更少, 波动范围稳定, 由此即可证实模型假设 2 的正确性。
\end{enumerate}
\begin{figure}[h]
    \centering
    \includegraphics[width=0.9\textwidth]{image15.png}  % 将宽度增加至 80% 的页面宽度
    \caption{残差Q-Q散点拟合}
    \label{fig:yield_comparison1}
\end{figure}

    \section{符号说明}  
    \label{sec:notation}  
    \centering  
    \begin{tabular}{c c}  
        \toprule  
        符号 & 符号含义\\  
        \midrule  
        $S_{i}$ & 第$i$种作物的种植面积/亩\\  
        $P_{i}(t)$ & 第$i$种作物在第$t$年的市场价格/元每斤\\  
        $P_i(T)$ & 第种作物在第年的市场价格(是一个随机变量，受到气候和需求波动的影响\\
        $Q_i(t)$ & 表示第$i$种作物在第年的培育成本/元\\
        $M_i^{(t)}$ & 表示第$i$种作物在第年的市场需求量/斤\\
        $A$ & 总共可种植面积/平方米\\
        $E\left[P_i(t)\right]$ & 农作物$i$在第$t$年的价格期望值/元\\
        $\mu_i$ & 第$i$种作物的价格增长率\\
        $\sigma_i$ & 第$i$种作物的价格波动率，代表价格波动幅度\\
        $d W_t$ & 标准布朗运动（也称之为正态分布随机变量），用于模拟价格波动\\
        $T$ & 未来的时间跨度/年（从2024年开始至2030年，$T=7$）\\
        $N$ & 模拟时间的步数/年\\
        $d t$ & 每个时间步的长度/年\\
        $R(T)$ & $2024-2030$作物的总收益/元\\
        $R_i(T)$ & 作物$i$在$2024-2030$的收益/元\\
        $G$ & 粮食作物的集合\\
        $R$ & 水稻的集合\\
        $m$ & 食用菌的集合\\
        $V$ & 蔬菜的集合\\
        $B$ & 豆类的集合\\
        $m$ & 地块数量\\
        $n$ & 农作物种类数量\\
        \bottomrule  
    \end{tabular}  
    
    \raggedright
    
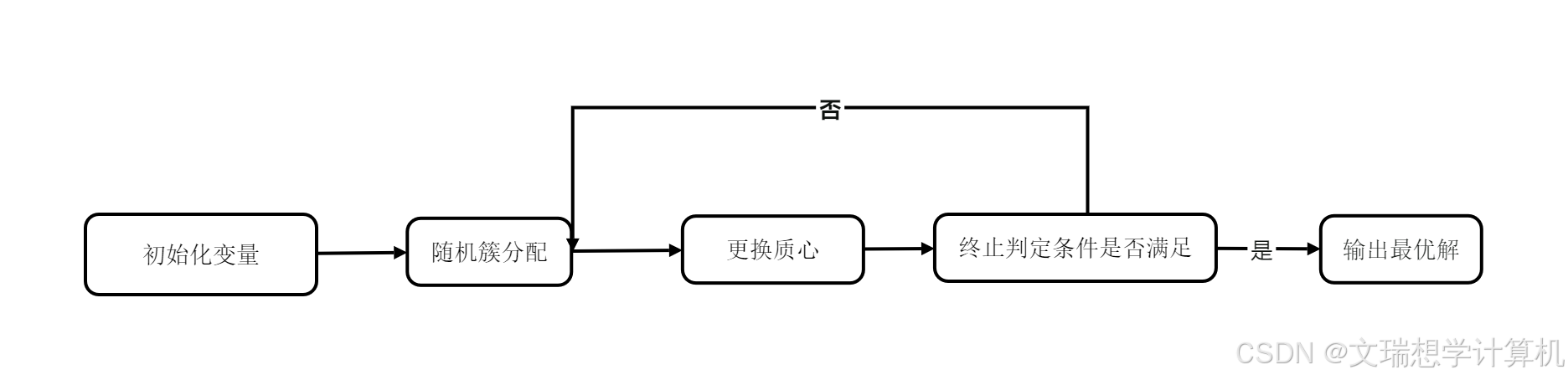
    \section{问题一求解}  
    \label{sec:solution1}  
       本题需要根据两个滞销产品处置方法分别设计算法求解最优种植策略，属于单目标多约束的混合整数线性规划。已知预期销售量、种植成本、亩产量和销售价格相较于2023年持平，我们给出以下实现步骤：
       
    \subsection{定义目标函数}
    \begin{equation}  
        \begin{aligned}  
            & \max R(T) = \sum_{t=2024}^{2030} \sum_{i=1}^n \left[ M_i^{(2023)} \cdot S_i + \left( \delta \cdot P_i(2023) - Q_i(2023) \right) \cdot S_i \right] \\  
            & \text{s.t.} \quad  
            \begin{cases}  
                \delta = 0, & \text{如果超过部分滞销，造成浪费} \\  
                \delta = 0.5, & \text{如果超过部分按2023年销售价50\%降价出售}  
            \end{cases}  
        \end{aligned}  
    \end{equation}  
    
    
    \subsection{条件约束}
    \subsubsection{种植面积总和约束}
    \begin{equation}
        \sum_{i=1}^N S_i \leq A
    \end{equation}

    \subsubsection{非负性约束}
    \begin{equation}\forall i, \quad S_i \geq 0\end{equation}
    
    \subsubsection{地块类型与用途约束}
    \setlength{\parindent}{2em}
    设 $x_{i, j}^{(t)}$ 为地块 j 在第 t 年种植第 i 种作物的二进制决策变量
    
    （1）露天耕地只能种植一季的粮食类作物设 $L_1$ 为露天耕地的地块索引集合，则对于每个 $j \in L_1$ ，有：
    
    \begin{equation}
    \forall j \in L_1, \quad \forall t, \quad \sum_{i \in G} x_{i, j}^{(t)} \leq 1
    \end{equation}
    
    （2）水浇地可以种植一季水稻或两季蔬菜设 $L_2$ 为水浇地的地块索引集合, 则对于每个 $j \in L_2$, 每年要么种一季水稻, 要么种两季蔬菜:
    
    \begin{equation}
    \forall j \in L_2, \quad \forall t, \quad \sum_{i \in R} x_{i, j}^{(t)}+\sum_{i \in V} x_{i, j}^{(t)} \leq 2
    \end{equation}
    
    
    （3）普通大棚只能种一季的蔬菜或一季的食用菌设 $L_3$ 为普通大棚地块索引的集合, 则对于每个 $j \in L_3$, 每年只能种植一季的蔬菜或一季的食用菌:
    
    \begin{equation}
    \forall j \in L_3, \quad \forall t, \quad \sum_{i \in V U M} x_{i, j}^{(t)} \leq 1
    \end{equation}
    
    （4）智慧大棚只能种两季的蔬菜设 $L_4$ 为智慧大棚的地块索引集合, 每年只能种两季蔬菜:
    
    \begin{equation}
    \forall j \in L_4, \quad \forall t, \quad \sum_{i \in V} x_{i, j}^{(t)}=2
    \end{equation}
    
    
    (3) 普通大棚只能种一季的蔬菜或一季的食用菌设 $L_3$ 为普通大棚地块索引的集合, 则对于每个 $j \in L_3$, 每年只能种植一季的蔬菜或一季的食用菌:
    
    \begin{equation}
    \forall j \in L_3, \quad \forall t, \quad \sum_{i \in V U M} x_{i, j}^{(t)} \leq 1
    \end{equation}
    
    （4）智慧大棚只能种两季的蔬菜
    设 $L_4$ 为智慧大棚的地块索引集合, 每年只能种两季蔬菜:
    
    \begin{equation}
    \forall j \in L_4, \quad \forall t, \quad \sum_{i \in V} x_{i, j}^{(t)}=2
    \end{equation}
\subsubsection{可持续性发展约束}
    （1）同一种类型地块不能连续重茬种植
    作物 $i$ 在地块 $j$ 上的种植不能连续发生在相邻的两年中:
    
    \begin{equation}
    \forall j \in L_{\varepsilon}(\varepsilon \in\{1,2,3,4\}), \quad \forall t, \quad \sum_{i \in X} x_{i, j}^{(t)}+\sum_{i \in X} x_{i, j}^{(t+1)} \leq 1
    \end{equation}
    
    $X$ 为单元素集合，且 $X \subseteq\{G, R, V, M\}$
    (2) 同种类型地块 3 年内不能没有豆类种植
    
    由已验证的假设知, 豆类作物经济效益极低, 故每连续三年内只有
    一年种植豆类作物:
    
    \begin{equation}
    \forall j \in L_{\varepsilon}(\varepsilon \in\{1,2,3,4\}), \quad \forall t, \quad \sum_{i \in B} x_{i, j}^{(t)}+\sum_{i \in B} x_{i, j}^{(t+1)}+\sum_{i \in B} x_{i, j}^{(t+2)}=1
    \end{equation}
    并且2024-2030年之间有两年种植豆类植物
    \begin{table}[htbp]
    \centering
    \begin{tabular}{|c|c|c|c|c|c|c|c|c|}
        \hline  
        年份 & 2023 & 2024 & 2025 & 2026 & 2027 & 2028 & 2029 & 2030 \\
        \hline
        方案 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\
        \hline
        方案 2 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\
        \hline
        方案 3 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\
        \hline
        方案 4 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\
        \hline
    \end{tabular}  
    \caption{不同年份的不同方案分析}
\end{table}
    \subsubsection{风险控制约束}
    
    使用在险价值 $(V a R)$ 度量工具进行风险限制， 在 $\alpha=95 \%$ 的置信水平下，设最低收益为 $R_0$, 则要求:
    
    \begin{equation}
    P\left(R_i(T)>R_0\right) \geq \alpha
    \end{equation}
    
    \begin{figure}[h]
        \centering
        \includegraphics[width=0.8\textwidth]{image19.png}  % 将宽度增加至 80% 的页面宽度
        \caption{遗传算法流程图}
        \label{fig:yield_comparison1}
    \end{figure}
    \subsection{遗传算法模型求解}
    \subsubsection{参数输入}
    基因初始化：每个基因随机取值 0, 0.5, 1 个体初始化：令个体 $\vec{x} \in \mathbb{R}^n, n$ 表示维数
    \subsubsection{种群生成}
    随机生成 m 个个体, 每个个体都是 n 维向量, 种群即:
    \begin{equation}
        \text{m} \times \text{n} \text{ 矩阵 } P = \left(\overrightarrow{x_1}, \overrightarrow{x_2}, \overrightarrow{x_3}, \ldots, \overrightarrow{x_m}\right)
    \end{equation}
    \subsubsection{适应度函数}
    目标是最大化利润 $R(T)$, 适应度函数为:
    
    \begin{equation}
    R(T)=\sum_{i=1}^n \operatorname{Profit}\left(\overrightarrow{x_i}\right)
\end{equation}
    
    $\operatorname{Profit}\left(\vec{x}_i\right)$ 是第 i 个基因对应的收益
    \subsubsection{交叉操作}
    本题使用两点交叉策略, 可描述为:
    
    \begin{equation}
    \overrightarrow{x_{\text {child }}}=\overrightarrow{x_{\text {parent } 1}^{\left[0: c_1\right]}}+\overrightarrow{x_{\text {parent } 2}^{\left[c_1: c_2\right]}}+\overrightarrow{x_{\text {parent } 1}^{\left[c_2: 0\right]}}
\end{equation}
    
    $c_1, c_2$ 是交叉点
    \subsubsection{变异操作}
    选择基于概率 p 的基因位翻转操作, 变异可描述为:
    
\begin{equation}
    \overrightarrow{x_{\text {new }}^{[i]}}=\left\{\begin{array}{cc}
        1-\overline{x^{[i]}} & \text { 概率为 } p \\
        \overline{x^{[i]}} & \text { 概率为 } 1-p
    \end{array}\right.
\end{equation}
    
    
    P取 0.05
    \subsubsection{选择操作}
    从当前种群中使用锦标赛选择法选择个体用于交又和变异:
    $\operatorname{Select}(t)=\operatorname{argmax}\left(\left\{R_i(T) \mid \overrightarrow{x_i} \in\right.\right.$ Tournament $\left.\}\right)$
    Tournament是从种群中随机选择个体的 3 元素集合
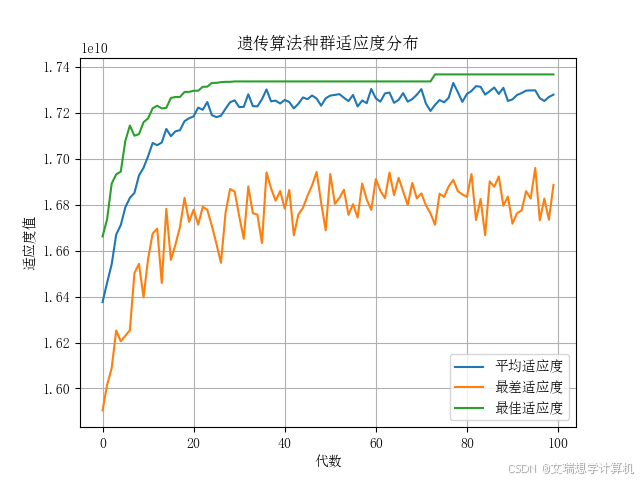
    \subsubsection{最优解图示}

\begin{figure}[h]
\centering
\includegraphics[width=0.9\textwidth]{image21.png}  % 将宽度增加至 80% 的页面宽度
\caption{最优解的种群分布}
\label{fig:yield_comparison1}
\end{figure}
    
    
    
    
    
    
    
    
    
    
    \section