布隆过滤器深度解析

最新推荐文章于 2025-05-18 19:14:41 发布

宁安我

最新推荐文章于 2025-05-18 19:14:41 发布

阅读量725

点赞数 26

文章标签：算法大数据数据结构布隆过滤器

本文链接：https://blog.csdn.net/2401_82505179/article/details/148030405

版权

大数据算法：布隆过滤器详解与实际应用

一、布隆过滤器简介

二、布隆过滤器的核心原理

1. 位数组（Bit Array）

2. 哈希函数（Hash Functions）

2. 使用计数布隆过滤器（Counting Bloom Filter）

3. 分层布隆过滤器（Layered Bloom Filter）

3. Redis 集成（Jedis 客户端）

八、布隆过滤器的扩展应用

1. 布谷鸟过滤器（Cuckoo Filter）

2. 空间效率优化

3. 分布式场景

九、总结

一、布隆过滤器简介

布隆过滤器（Bloom Filter）是一种空间效率极高的概率型数据结构，由 Burton Howard Bloom 于 1970 年提出。它通过位数组和多个哈希函数的组合，实现对元素是否存在性的快速判断。其核心特性是：

空间高效：相比传统集合存储结构（如哈希表），布隆过滤器的存储开销极低。
查询快速：插入和查询的时间复杂度均为 O(k)O(k)（kk 为哈希函数数量）。
允许误判：存在假阳性（False Positive），但绝不会漏判（False Negative）。

布隆过滤器广泛应用于大数据场景，例如：

缓存系统：防止缓存穿透。
网络爬虫：去重已抓取的 URL。
垃圾邮件过滤：快速判断邮件地址是否合法。
数据库优化：加速大规模数据查询。

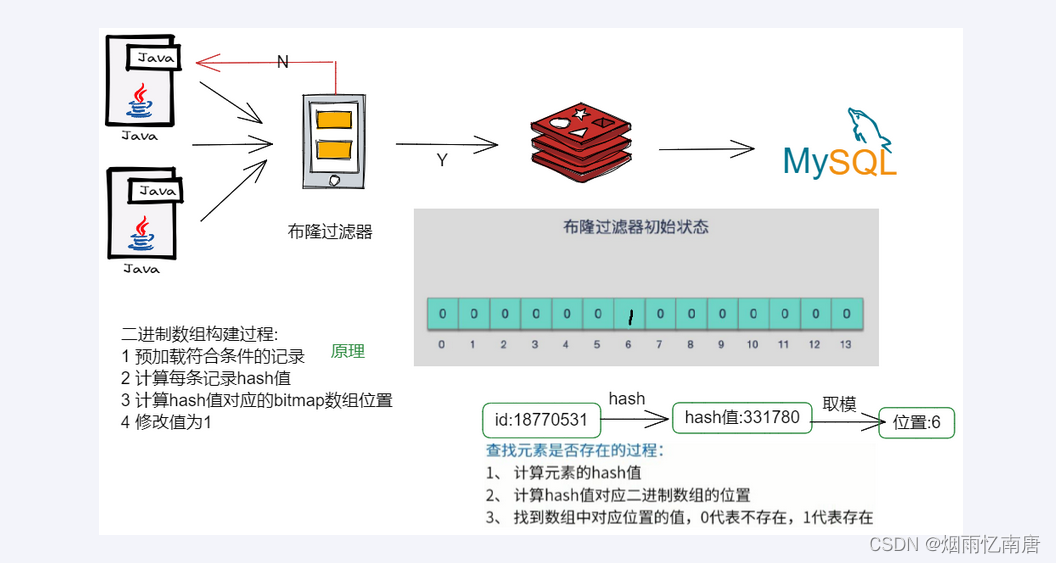
二、布隆过滤器的核心原理

1. 位数组（Bit Array）

布隆过滤器的核心是一个长度为 mm 的位数组（bit array），初始时所有位均为 0。

2. 哈希函数（Hash Functions）

使用 kk 个独立的哈希函数，将元素映射到位数组的 kk 个位置，并将这些位置设置为 1。

3. 插入操作

对于插入的元素 xx，计算 kk 个哈希值 h_1(x), h_2(x), \dots, h_k(x)h1(x),h2(x),…,hk(x)。
将位数组中对应位置设置为 1。

4. 查询操作

对于查询的元素 xx，计算相同的 kk 个哈希值。
如果所有对应位置的位均为 1，则认为 xx 可能存在于集合中。
如果存在任意一个位为 0，则 xx 一定不存在于集合中。

5. 误判率

布隆过滤器的误判率（False Positive Rate）由以下公式决定：

其中：

nn为插入元素数量。
m 为位数组长度。
k为哈希函数数量。

三、布隆过滤器的实现细节

1. 参数选择

位数组大小 mm：根据预期元素数量 nn 和可接受的误判率 pp 计算。
哈希函数数量 kk：通常取 k = \frac{m}{n} \ln 2k=nmln2。

2. 哈希函数设计

需要选择多个独立且分布均匀的哈希函数。
常用哈希算法：FNV、MurmurHash、SHA 等。

3. 动态扩容

传统布隆过滤器不支持动态扩容，但可以通过以下方式改进：

分层布隆过滤器：当容量不足时，增加新的布隆过滤器。
概率调整：动态调整哈希函数数量或位数组长度。

四、布隆过滤器的实际应用案例

案例 1：缓存系统中的防缓存穿透

场景：在缓存系统（如 Redis）中，频繁查询不存在的键会导致数据

最低0.47元/天解锁文章