最优二叉树（哈夫曼树）

哈夫曼树定义：

叶子结点的权值是对叶子结点赋予的一个有意义的数值量，设二叉树具有n个带权值的叶子结点，从根节点到各个叶子结点的路径长度与相应叶子结点权值的乘机之和称为二叉树的带权路径长度。带权路径最小的二叉树称为最优二叉树，也称哈夫曼树。

最优二叉树有什么特点?

1.权值越大的叶子结点越靠近根节点

2.只有度为0和度为2的结点，不存在度为1的结点

基本思想：

1. 初始化：由 n 个权值构造 n 棵只有一个根结点的二叉树，得到一个二叉树集合 F＝{T1，T2，…，Tn}；

2. 重复下述操作，直到集合 F 中只剩下一棵二叉树

    2.1 选取与合并：在 F 中选取根结点的权值最小的两棵二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根结点的权值为其左右子树根结点的权值之和.

 2.2 删除与加入：在 F 中删除作为左右子树的两棵二叉树，并将新建立的二叉树加入到F中；

初始化                                                             选取与合并               删除与加入

                     

                   

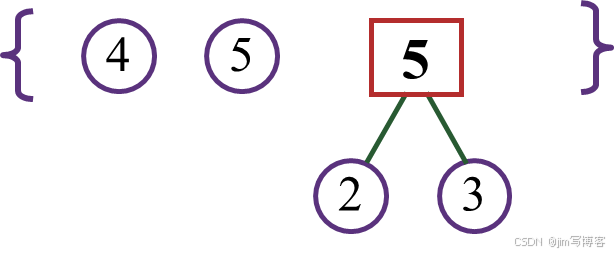
如何存储哈夫曼树呢？

需要存储的关系

struct ElemType

{

    int weight;               /*假定权值为整数*/

    int parent, lchild, rchild;

};

表示哈夫曼树：

创建一个数组，可以推算出数组大小为2n-1，每个数组元素为一个哈夫曼元素，lchild，rchild,parent,weight.

哈夫曼树的查找算法：

构建哈夫曼树时，需要每次根据各个结点的权重值，筛选出其中值最小的两个结点，然后构建二叉树。

查找权重值最小的两个结点的思想是：从树组起始位置开始，首先找到两个无父结点的结点（说明还未使用其构建成树），然后和后续无父结点的结点依次做比较，有两种情况需要考虑：

如果比两个结点中较小的那个还小，就保留这个结点，删除原来较大的结点；
如果介于两个结点权重值之间，替换原来较大的结点；

//HT数组中存放的哈夫曼树，end表示HT数组中存放结点的最终位置，s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int *s1, int *s2)
{
    int min1, min2;
    //遍历数组初始下标为 1
    int i = 1;
    //找到还没构建树的结点
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    min1 = HT[i].weight;
    *s1 = i;
   
    i++;
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    //对找到的两个结点比较大小，min2为大的，min1为小的
    if(HT[i].weight < min1){
        min2 = min1;
        *s2 = *s1;
        min1 = HT[i].weight;
        *s1 = i;
    }else{
        min2 = HT[i].weight;
        *s2 = i;
    }
    //两个结点和后续的所有未构建成树的结点做比较
    for(int j=i+1; j <= end; j++)
    {
        //如果有父结点，直接跳过，进行下一个
        if(HT[j].parent != 0){
            continue;
        }
        //如果比最小的还小，将min2=min1，min1赋值新的结点的下标
        if(HT[j].weight < min1){
            min2 = min1;
            min1 = HT[j].weight;
            *s2 = *s1;
            *s1 = j;
        }
        //如果介于两者之间，min2赋值为新的结点的位置下标
        else if(HT[j].weight >= min1 && HT[j].weight < min2){
            min2 = HT[j].weight;
            *s2 = j;
        }
    }
}

算法描述:

    for (i = 0; i < n; i++)

        huffTree[i].weight = w[i];

哈夫曼编码：（为了获得最经济的编码方案）

采用哈夫曼编码构造的编码是一种能使字符串的编码总长度最短的不等长编码

设字符集为{d1,d2,d3..dn},他们在字符串中出现的频率为{w1,w2,w3...wn}d1,d2...dn作为叶子结点，w1,w2,...wn作为叶子结点的权值，构造一棵哈夫曼树，规定哈夫曼树的左分支代表0，右分支代表1，则从根节点到叶子结点所经过的路径组成的0和1序列便是叶子节点对应字符的编码。