scikit-learn基础用法

一.数据引入

获取数据的方式：

• 获取小数据集(本地加载)：datasets.load_xxx( )
• 获取大数据集(在线下载)：datasets.fetch_xxx( )
• 本地生成数据集(本地构造)：datasets.make_xxx( )

• 补充：

  大数据集是规模庞大、复杂多样的数据集合。特点是数据量巨大,通常以TB、PB甚至EB为单位进行计量。小数据集：规模较小的数据集合。特点是数据量相对较小,通常以GB或者更小的单位进行计量。

  数据集	介绍
  load_iris( )	鸢尾花数据集：3类、4个特征、150个样本
  load_boston( )	波斯顿房价数据集：13个特征、506个样本
  load_digits( )	手写数字集：10类、64个特征、1797个样本
  load_breast_cancer( )	乳腺癌数据集：2类、30个特征、569个样本
  load_diabets( )	糖尿病数据集：10个特征、442个样本
  load_wine( )	红酒数据集：3类、13个特征、178个样本
  load_files( )	加载自定义的文本分类数据集
  load_linnerud( )	体能训练数据集：3个特征、20个样本
  load_sample_image( )	加载单个图像样本，只有'china'和'flower'两张图片
  load_svmlight_file( )	加载svmlight格式的数据
  make_blobs( )	生成多类单标签数据集
  make_biclusters( )	生成双聚类数据集
  make_checkerboard( )	生成棋盘结构数组，进行双聚类
  make_circles( )	生成二维二元分类数据集
  make_classification( )	生成多类单标签数据集
  make_friedman1( )	生成采用了多项式和正弦变换的数据集
  make_gaussian_quantiles( )	生成高斯分布数据集
  make_hastie_10_2( )	生成10维度的二元分类数据集
  make_low_rank_matrix( )	生成具有钟形奇异值的低阶矩阵
  make_moons( )	生成二维二元分类数据集
  make_multilabel_classification( )	生成多类多标签数据集
  make_regression( )	生成回归任务的数据集
  make_s_curve( )	生成S型曲线数据集
  make_sparse_coded_signal( )	生成信号作为字典元素的稀疏组合
  make_sparse_spd_matrix( )	生成稀疏堆成的正定矩阵
  make_sparse_uncorrelated( )	使用稀疏的不相关设计生成随机回归问题
  make_spd_matrix( )	生成随机堆成的正定矩阵
  make_swiss_roll( )	生成瑞士卷曲线数据集

  代码演示

  from sklearn import datasets
  import matplotlib.pyplot as plt
  
  # 鸢尾花数据演示
  iris = datasets.load_iris()  # 加载鸢尾花数据集
  features = iris.data  # 提取数据集的特征
  target = iris.target  # 提取数据集的目标
  print(features.shape, target.shape)  # 打印特征和目标的形状
  print(iris.feature_names)  # 打印特征的名称
  
  # 手写数字图片演示
  digits = datasets.load_digits()  # 加载手写数字图片数据集
  print(digits.data.shape)  # 打印手写数字图片数据集的形状
  plt.gray()  # 设置颜色为灰色
  plt.imshow(digits.images[2])  # 显示手写数字图片数据集中的第三张图片
  plt.show()
  
  # 生成圆形数据
  x, y = datasets.make_circles(n_samples=15000, shuffle=True, noise=0.03)  
  # 生成圆形数据x,y坐标
  plt.scatter(x[:, 0], x[:, 1], c=y, s=7)  # 绘制圆形数据的散点图
  plt.show()
  
  # 生成瑞士卷型数据
  X, t = datasets.make_swiss_roll(n_samples=2000, noise=0.1)  # 生成瑞士卷型数据x,y坐标
  fig = plt.figure()  # 创建一个新的图形
  ax = fig.add_subplot(111, projection='3d')  # 添加一个3D子图
  ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.Spectral, edgecolors='black')  
  # 绘制瑞士卷型数据的3D散点图
  plt.show()
  
  # 展示示例图片
  img = datasets.load_sample_image('flower.jpg')  # 加载示例图片"flower.jpg"
  print(img.shape)  # 打印示例图片的形状
  plt.imshow(img)  # 显示示例图片
  plt.show()

  报错提醒

• 解决：

• 避免这个报错，需要Ctrl+shift 将输入法切换，不使用搜狗输入法下运行，报错就没了。

     演示结果

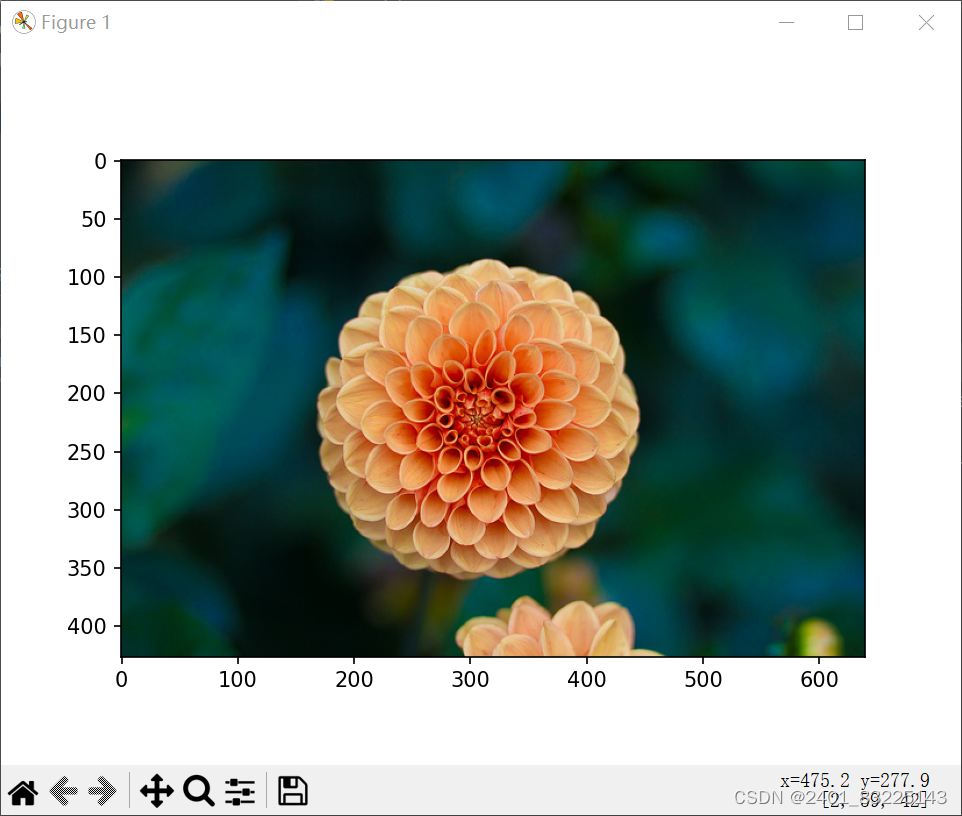二. 数据预处理

函数	功能
preprocessing.scale( )	标准化
preprocessing.MinMaxScaler( )	最大最小值标准化
preprocessing.StandardScaler( )	数据标准化
preprocessing.MaxAbsScaler( )	绝对值最大标准化
preprocessing.RobustScaler( )	带离群值数据集标准化
preprocessing.QuantileTransformer( )	使用分位数信息变换特征
preprocessing.PowerTransformer( )	使用幂变换执行到正态分布的映射
preprocessing.Normalizer( )	正则化
preprocessing.OrdinalEncoder( )	将分类特征转换为分类数值
preprocessing.LabelEncoder( )	将分类特征转换为分类数值
preprocessing.MultiLabelBinarizer( )	多标签二值化
preprocessing.OneHotEncoder( )	独热编码
preprocessing.KBinsDiscretizer( )	将连续数据离散化
preprocessing.FunctionTransformer( )	自定义特征处理函数
preprocessing.Binarizer( )	特征二值化
preprocessing.PolynomialFeatures( )	创建多项式特征
preprocessing.Imputer( )	弥补缺失值

 （一）标准化

含义：

公式为=(X-mean)/std  计算时对每个属性/每列分别进行。

将数据按期属性（按列进行）减去其均值，并处以其方差。得到的结果是，对于每个属性/每列来说所有数据都聚集在0附近，方差为1。

preprocessing.scale( )

import numpy as np
from sklearn import preprocessing

# 标准化：将数据转换为均值为0，方差为1的数据，即标注正态分布的数据
x = np.array([[1, -1, 2],
              [2, 0, 0],
              [0, 1, -1]])
x_scale = preprocessing.scale(x)
# 标准化数组
print(x_scale)

# 处理后数据的均值和方差
print(x_scale.mean(axis=0))
print(x_scale.std(axis=0))
# axis=0 是独立的标准化每个特征

运行结果

preprocessing.StandardScaler( )

好处：

使用该类的好处在于可以保存训练集中的参数（均值、方差）直接使用其对象转换测试集数据。

scale = preprocessing.StandardScaler().fit(x)
scale_std = scale.transform(x)
print(scale_std)
print(scale_std.mean(axis=0))
print(scale_std.std(axis=0)))

 （二）数据特征缩放

含义：

是用于将数据特征进行缩放的函数。它将特征的值映射到一个给定的范围（默认为[0, 1]），通过对数据进行线性变换，使得数据落入指定的范围内，并且保留原始数据的分布关系。

1. 导入MinMaxScaler类：from sklearn.preprocessing import MinMaxScaler

2. 创建MinMaxScaler对象：scaler = MinMaxScaler()

3. 调用fit_transform()方法进行数据的缩放：scaled_data = scaler.fit_transform(data)

   - fit_transform()方法将对数据进行拟合和转换操作，返回缩放后的数据。

   - fit()方法用于拟合数据，find the minimum and maximum of each feature.

   - transform()方法用于进行数据的缩放。

4. 可用inverse_transform()方法将缩放后的数据转换为原始数据：

original_data = scaler.inverse_transform(scaled_data)

# 数据缩放
scaler = preprocessing.MinMaxScaler()
scaled_data = scaler.fit_transform(x)
# 缩放后的数据
print(scaled_data)
# 均值和方差
print(scaled_data.mean(axis=0),scaled_data.std(axis=0))
# 还原数据
original_data = scaler.inverse_transform(scaled_data)
print(original_data)

运行结果

 （三）正则化

说明：

归一化和标准化是对数据集中的列进行的操作，而正则化是对数据集中的行进行的操作。

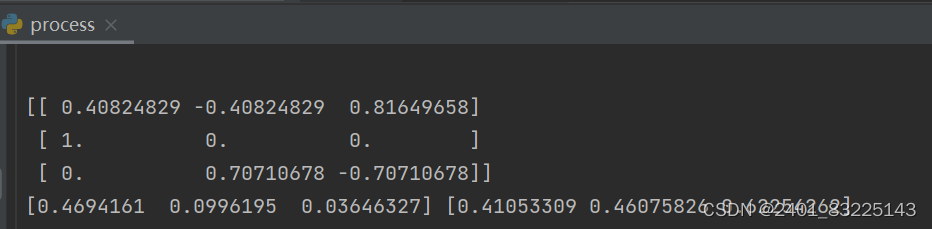
# 正则化
nor_scale = preprocessing.Normalizer()
x_nor = nor_scale.fit_transform(x)
print(x_nor)
print(x_nor.mean(axis=0),x_nor.std(axis=0))

运行结果

 （四）独热编码

含义：

是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后，每个整数值被表示为二进制向量，除了整数的索引之外，它都是零值，它被标记为1。

举例：

球类特征：["足球"，"篮球"，"羽毛球"，"乒乓球"]（这里N=4）：

足球  =>  1000

篮球  =>  0100

羽毛球  =>  0010

乒乓球  =>  0001

# 将分类特征或数据标签转换位独热编码
ohe = preprocessing.OneHotEncoder()
x1 = ([["大象"],["猴子"],["老虎"],["老鼠"]])
x_ohe1 = ohe.fit(x1).transform([["大象"]]).toarray()
x_ohe2 = ohe.fit(x1).transform([["猴子"]]).toarray()
x_ohe3 = ohe.fit(x1).transform([["老虎"]]).toarray()
x_ohe4 = ohe.fit(x1).transform([["老鼠"]]).toarray()
print(x_ohe1)
print(x_ohe2)
print(x_ohe3)
print(x_ohe4)

运行结果

三.算法的选择

对于分类、回归、聚类、降维算法的选择，可以参照下图中的算法选择路径图：

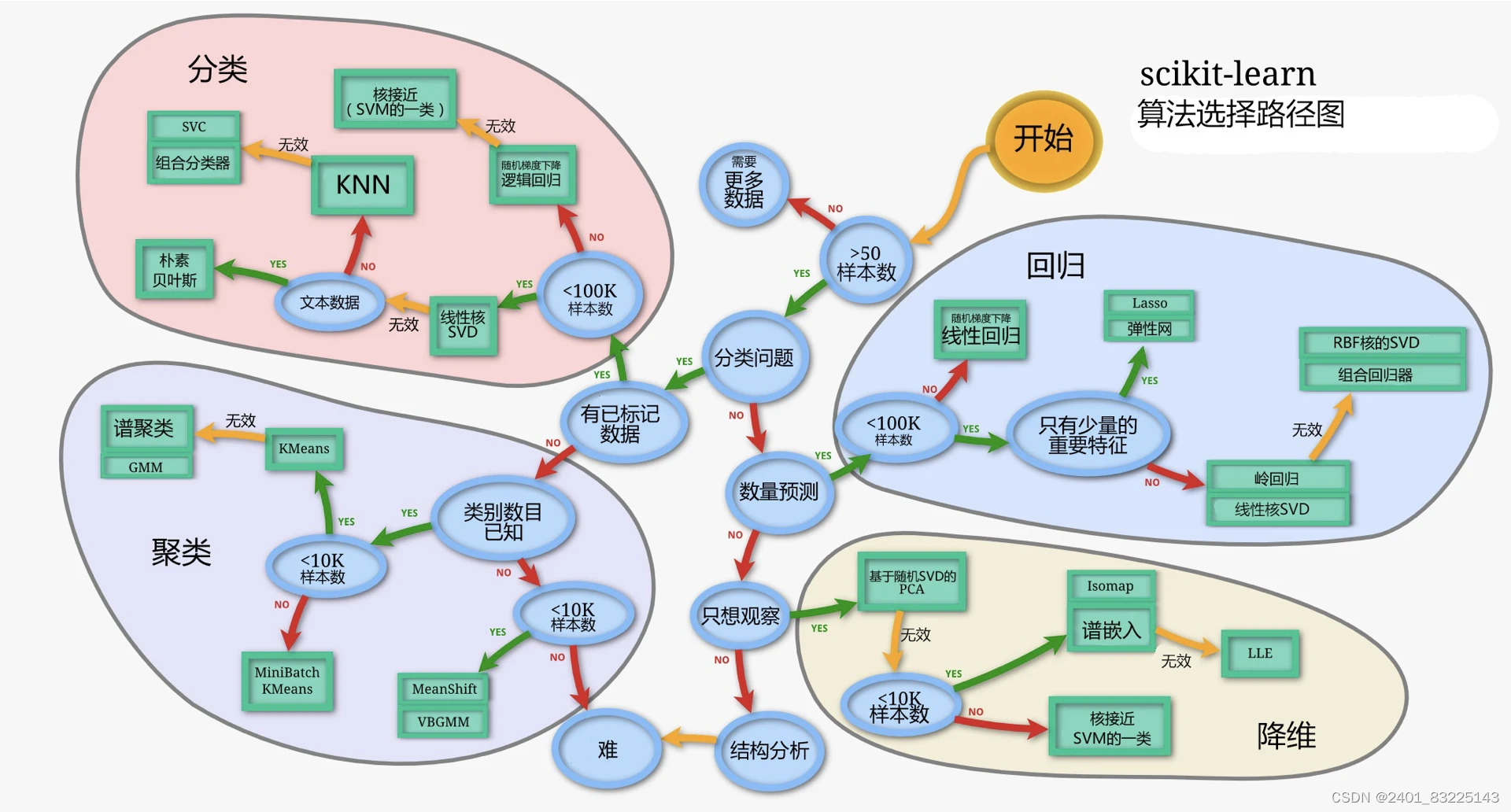
从图中可以看到，按照是否为分类问题划分成了两大块，其中分类和聚类属于分类的问题（虽然聚类没有给定类别），回归和降维属于非分类的问题。同时，四类算法也可以按照数据是否有标签划分为监督学习（分类、回归）和无监督学习（聚类、降维）。

四.数据划分

（一）训练误差和泛化误差

训练误差：出自于训练数据
泛化误差：出自于新数据
比如说，使用历年考试真题准备将来的考试，在历年考试真题取得好成绩（训练误差）并不能保证未来考试成绩好（泛化误差），我们训练模型的目的是希望训练好的模型泛化误差越低越好。

（二）验证数据集和测试数据集

下图是机器学习实操的7个步骤：

划分数据集一般包括三个部分：

• 验证数据集（Validation Dataset）：用于评估模型的数据集，不应与训练数据混在一起
• 测试数据集（Test Dataset）：只可以使用一次数据集
• 训练数据集（Training Dataset）：用于训练模型的数据集

 为什么划分数据集：

首先我们知道训练模型的目的是使得模型的泛化能力越来越强（泛化能力是指机器学习算法对新鲜样本的适应能力），在训练集上，我们不断进行前向转播和反向传播更新参数使得在训练误差越来越小，但是这并不能代表这个模型泛化能力很强，因为它只是在拟合一个给定的数据集（就好比做数学题用背答案的办法，正确率很高，但并不代表你学到了东西），那么如何评判这个模型泛化能力强呢？就用到了测试数据集，测试数据集就像是期末考试，在模型最终训练完成后才会使用一次，在最终评估之前不能使用这个数据集（好比在考试前不能泄题一样）。判断模型泛化能力强弱的途径有了，但是我们知道在神经网络中有很多超参数也会对模型泛化能力造成影响，那么如何判断不同参数对模型的影响呢，毕竟测试集只能用一次，而参数调整需要很多次，而且也不能使用训练数据集，这样只会拟合训练数据集，无法证明其泛化能力提升，于是我们又划分出了一个数据集，验证数据集，我们的模型训练好之后用验证集来看看模型的表现如何，同时通过调整超参数，让模型处于最好的状态。

用一个比喻来说：

• 训练集相当于上课学知识
• 验证集相当于课后的的练习题，用来纠正和强化学到的知识
• 测试集相当于期末考试，用来最终评估学习效果

（三）划分数据集 

scikit-learn有很多划分数据集的方法，它们都在model_selection 里面。

常用的有：

• K折交叉验证：

• 含义：k折交叉验证先将数据集D随机划分为 k个大小相同的互斥子集，即 ，每次随机的选择 k-1份作为训练集，剩下的1份做测试集。当这一轮完成后，重新随机选择 k份来训练数据。若干轮（小于 k ）之后，选择损失函数评估最优的模型和参数。注意，交叉验证法评估结果的稳定性和保真性在很大程度上取决于 k取值。

• • KFold 普通K折交叉验证
  • StratifiedKFold（保证每一类的比例相等）

• 留一法：

• 含义：它将原始数据集划分成两个互斥的集合，一个作为训练集，另一个作为测试集。具体操作时，根据实际需求把原始数据按比例分成两部分：一部分用来训练模型，另一部分用于验证模型。

• • LeaveOneOut （留一）
  • LeavePOut （留P验证，当P = 1 时变成留一法）

• 随机划分法：

• • ShuffleSplit （随机打乱后划分数据集）
  • StratifiedShuffleSplit （随机打乱后，返回分层划分，每个划分类的比例与样本原始比例一致）

以上的划分方法各有各的优点，留一法、K折交叉验证充分利用了数据，但开销比随机划分要高，随机划分方法可以较好的控制训练集与测试集的比例,（通过设置train_size参数）详细可查看官方文档。

# 简单划分数据
# 导入所需库
from sklearn.model_selection import train_test_split
from sklearn import datasets
import pandas as pd

# 加载鸢尾花数据集
X, y = datasets.load_iris(return_X_y=True)

# 使用train_test_split函数划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 打印训练集和测试集的形状
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

# K折交叉验证
# 导入所需库
from sklearn.model_selection import KFold
import numpy as np

# 创建一个示例数组
X = np.random.randint(1, 10, 20)

# 初始化KFold对象，将数据集分成5折
kf = KFold(n_splits=5)

# 遍历训练集和测试集的索引
for train, test in kf.split(X):
    print(train, '\n', test)

# 留一法划分数据
# 导入所需库
from sklearn.model_selection import LeaveOneOut
import numpy as np

# 创建一个示例数组
X = np.random.randint(1, 10, 5)

# 初始化LeaveOneOut对象，使用留一法划分数据
kf = LeaveOneOut()

# 遍历训练集和测试集的索引
for train, test in kf.split(X):
    print(train, '\n', test)

pandas安装

方法一：

方法二：

anaconda终端安装

报错提示1：

解决方法：网络不好，更换网络，再安装一次。

报错提示2：

解决方法：更新pip。

使用划分后的数据集进行训练：

运行结果：

指标说明：

precision（精准率）：指在所有被模型预测为正例的样本中，实际为正例的比例。

recall（召回率）：指在所有实际为正例的样本中，被模型正确预测为正例的比例。

F1-score（F1分数）：是统计学中用来衡量二分类模型精确度的一种指标。

support（支持度）：支持度表示项集{X,Y}在总项集里出现的概率。