
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
=
r
v
⃗
定
义
:
v
⃗
=
x
i
y
j
z
k
\mathbb{q}=r+\vec{v} \[2ex] 定义:\vec{v} = xi+yj+zk
q=r+v
定义:v
=xi+yj+zk
注意其中x,y,z,w的定义方式,其实这也正是我们在计算机程序中用XMFLOAT4表示四元数元素的顺序,也是我们在Shader中表示四元数的顺序。即最后一个分量w代表四元数的实部。关于四元数的其它相关知识大家可以去搜资料复习一下,这里就不多费篇幅了,重点放在四元数的使用上。
首先我们回到刚才的问题,即具体的我们如何用四元数来表示绕任意轴的旋转呢?
假
设
要
旋
转
的
轴
为
n
⃗
,
并
且
是
归
一
化
的
单
位
向
量
,
同
时
绕
该
轴
的
旋
转
为
θ
,
那
么
用
四
元
数
可
以
表
达
这
一
旋
转
如
下
:
q
=
[
c
o
s
(
θ
2
)
,
n
⃗
x
s
i
n
(
θ
2
)
,
n
⃗
y
s
i
n
(
θ
2
)
,
n
⃗
z
s
i
n
(
θ
2
)
]
=
[
c
o
s
(
θ
2
)
,
s
i
n
(
θ
2
)
n
⃗
]
假设要旋转的轴为 \ \vec{n} \ ,并且是归一化的单位向量,同时绕该轴的旋转为 \theta , 那么用四元数可以表达这一旋转如下: \[2ex] \mathbb{q}=[ cos(\frac{\theta}{2}),\ \vec{n}_x sin(\frac{\theta}{2}),\ \vec{n}_y sin(\frac{\theta}{2}),\ \vec{n}_z sin(\frac{\theta}{2}) ] \[2ex] = [ cos(\frac{\theta}{2}),\ sin(\frac{\theta}{2})\vec{n}]
假设要旋转的轴为 n
,并且是归一化的单位向量,同时绕该轴的旋转为θ,那么用四元数可以表达这一旋转如下:q=[cos(2θ), n
xsin(2θ), n
ysin(2θ), n
zsin(2θ)]=[cos(2θ), sin(2θ)n
]
这样,一个围绕轴
n
⃗
的
θ
\vec{n}的\theta
n
的θ角度的旋转就被简单且直观的表达出来了。注意这里的四元数是个单位四元数,其“模”等于1。
其次,这样表达之后有什么好处呢?
1、因为这样的四元数都是单位四元数,所以连乘后结果依然保持“模”为1的单位归一性。
2、当将一般的3D向量表示为实部为0的四元数时
v
⃗
=
[
0
,
(
x
,
y
,
z
)
]
\vec{v}=[0,(x,y,z)]
v
=[0,(x,y,z)]时,用单位四元数旋转该向量可以简单的表示为:
q
=
q
=
[
c
o
s
(
θ
2
)
,
n
⃗
x
s
i
n
(
θ
2
)
,
n
⃗
y
s
i
n
(
θ
2
)
,
n
⃗
z
s
i
n
(
θ
2
)
]
则
:
v
⃗
′
=
q
v
⃗
q
−
1
其
中
:
q
−
1
=
q
∗
∥
q
∥
q
∗
=
(
r
v
⃗
)
∗
=
(
r
−
v
⃗
)
=
[
w
−
x
i
−
y
i
−
z
i
]
∵
∥
q
∥
=
1
∴
q
−
1
=
[
c
o
s
(
θ
2
)
,
−
n
⃗
x
s
i
n
(
θ
2
)
,
−
n
⃗
y
s
i
n
(
θ
2
)
,
−
n
⃗
z
s
i
n
(
θ
2
)
]
\mathbb{q}=\mathbb{q}=[ cos(\frac{\theta}{2}),\ \vec{n}_x sin(\frac{\theta}{2}),\ \vec{n}_y sin(\frac{\theta}{2}),\ \vec{n}_z sin(\frac{\theta}{2}) ] \[2ex]则: \vec{v}^{'} = \mathbb{q} \vec{v} \mathbb{q}^{-1} \[2ex] 其中:\mathbb{q}^{-1} = \frac{\mathbb{q}^*}{\begin{Vmatrix}\mathbb{q}\end{Vmatrix}} \qquad \mathbb{q}^* = (r+\vec{v})^{*}=(r-\vec{v})=[w - xi -yi -zi] \[2ex] \because \begin{Vmatrix}\mathbb{q}\end{Vmatrix} = 1 \[2ex] \therefore \mathbb{q}^{-1} = [ cos(\frac{\theta}{2}),\ -\vec{n}_x sin(\frac{\theta}{2}),\ -\vec{n}_y sin(\frac{\theta}{2}),\ -\vec{n}_z sin(\frac{\theta}{2}) ]
q=q=[cos(2θ), n
xsin(2θ), n
ysin(2θ), n
zsin(2θ)]则:v
′=qv
q−1其中:q−1=∥∥q∥∥q∗q∗=(r+v
)∗=(r−v
)=[w−xi−yi−zi]∵∥∥q∥∥=1∴q−1=[cos(2θ), −n
xsin(2θ), −n
ysin(2θ), −n
zsin(2θ)]
上面的式子说明用四元数来生成向量的旋转也十分的简单和直观(这里的旋转操作可以形象的理解为沿着轴正向先顺时针旋转二分之一角度,再沿着轴负向继续顺时针旋转二分之一角度,这样整体上看就是延着轴旋转了指定的角度
θ
\theta
θ。这样的过程本身就避免了“左乘”还是“右乘”的问题,变成了“左右都乘一半”的对称形式!需要注意的是如果是从负轴向看过去其实应该是“逆时针旋转”。)。
<div align=center>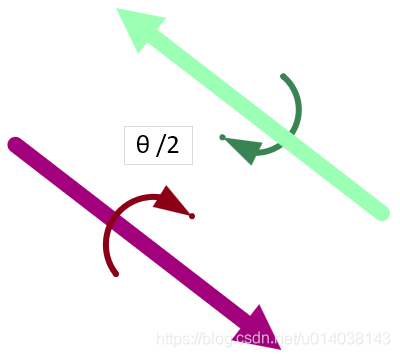
3、实质上,四元数最常用的就是对其进行插值,进而表达用绕一个轴旋转一定角度“平滑”变换到绕另一个轴的旋转,四元数插值有以下两种(实质上还有一种NSlep,就是基于第一种线性插值后再取“模”,也不很常用就不介绍了):
设
有
两
个
单
位
四
元
数
q
1
和
q
2
,
则
普
通
线
性
插
值
(
l
e
r
p
)
:
q
t
=
(
1
−
t
)
q
1
t
q
2
“
平
滑
”
插
值
(
球
面
线
性
插
值
,
S
l
e
r
p
)
:
q
t
=
s
i
n
(
(
1
−
t
)
φ
)
s
i
n
(
φ
)
q
1
s
i
n
(
t
φ
)
s
i
n
(
φ
)
q
2
其
中
:
φ
=
c
o
s
(
q
1
⋅
q
2
)
−
1
,
即
两
个
四
元
数
间
的
夹
角
设有两个单位四元数\ \mathbb{q_1} \ 和 \ \mathbb{q_2} ,\ 则普通线性插值(lerp): \[2ex] \mathbb{q_t} = (1 - t)\mathbb{q_1} + t\mathbb{q_2} \[2ex] “平滑”插值(球面线性插值,Slerp): \[2ex] \mathbb{q_t} = \frac{sin((1 - t)\varphi)}{sin(\varphi)}\mathbb{q_1} + \frac{sin( t\varphi)}{sin(\varphi)}\mathbb{q_2} \[2ex] 其中: \varphi = cos(\mathbb{q_1} \cdot \mathbb{q_2})^{-1},即两个四元数间的夹角
设有两个单位四元数 q1 和 q2, 则普通线性插值(lerp):qt=(1−t)q1+tq2“平滑”插值(球面线性插值,Slerp):qt=sin(φ)sin((1−t)φ)q1+sin(φ)sin(tφ)q2其中:φ=cos(q1⋅q2)−1,即两个四元数间的夹角
实际使用时我们常用的是第二个插值公式“球面线性插值”,即它保持了插值过程中产生的中间四元数仍然是单位四元数的性质,而第一个直接的线性插值会导致中间四元数的“模”不为1的情况,会给我们的计算带来麻烦。幸运的是在DirectXMath中已经准备了四元数插值的函数:XMQuaternionSlerp。最终怎么理解“平滑”的插值这个含义呢?见下图:
<div align=center>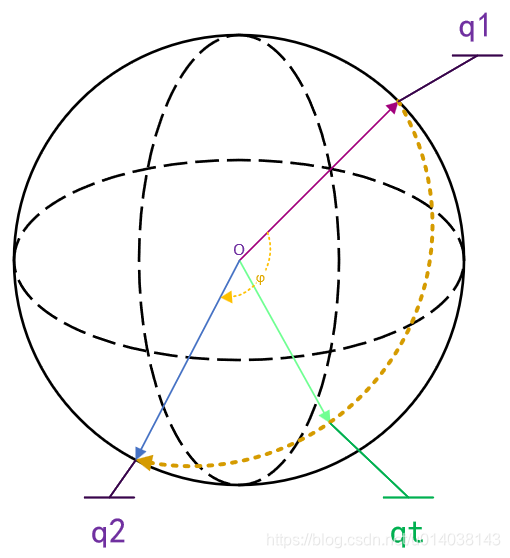
从图中可以看出,四元数球面线性插值很好的保证了旋转插值的“平滑”性,即中间结果
q
t
q_{t}
qt总是在单位球面上,并且最终路径总是单位球体的”大圆“上。这也很符合我们对旋转运动的最直观的感知,所以用四元数插值来模拟方位的变换就具有天然的优势。而使用其它的表达方式如使用向量、或矩阵,很难做到这样简单的”平滑“插值,尤其是矩阵根本没法简单进行插值。由于画图的局限性,这里大家要注意的是,球面线性插值还对“绕轴”的旋转也做了平滑的插值。如下图中,注意以玩偶头部鼻尖方向为轴,注意其中的旋转变化:
<div align=center>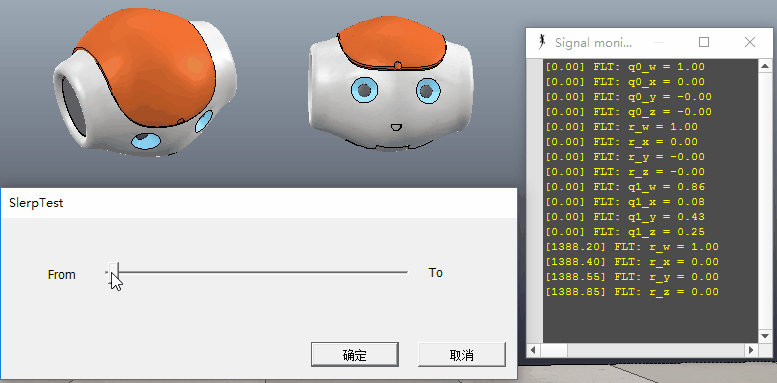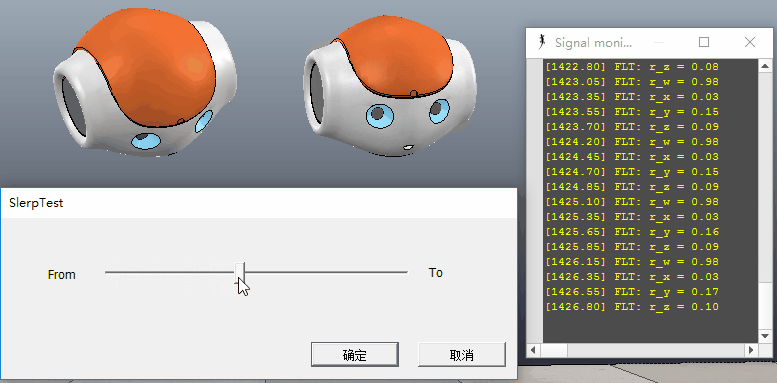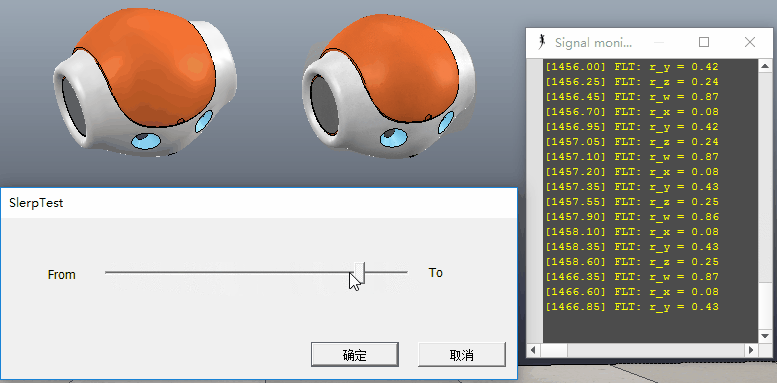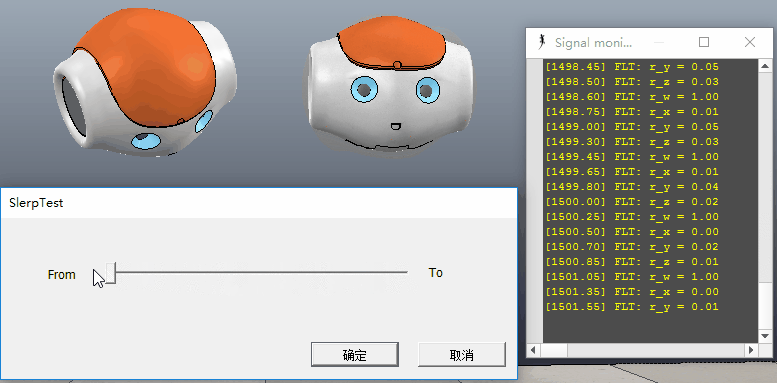
4、最后,四元数也可以转换到等价变换矩阵形式,其公式就不啰嗦了,因为基本也是不易“理解”和不直观的。并且在DirectXMath中也为我们准备好了函数:XMMatrixRotationQuaternion,可以方便的完成四元数到矩阵的转换,直接调用即可。再次提醒各位的就是,DirectXMath甚至Assimp中,在用4维向量表示四元数时,最终w分量也就是最后一个分量总是四元数的实部!这几乎是所有3D数学库的默认约定!
9.2、SQT变换综合
搞明白了四元数以及最最重要的球面线性插值之后,我们回过头来看一下基本的三种变换的最终表示。对于缩放来说用一个3维向量的x、y、z分量即可表示每个轴上的缩放,当然前提是坐标轴对齐了相应的缩放方向。而平移也可以用另一个3维向量来表示各个轴向的位移大小,同样也是要求坐标轴对齐位移方向。最终如果这两个坐标轴向不能简单的取得一致时,就在中间加入一个表示旋转的四元数变换即可!而这就是骨骼动画中经典的SQT变换的由来:Scale、Quaternion、Translation。最后,分别使用这三个变换生成对应的变换矩阵,进行矩阵连乘,就表示一个复合变换,然后替换到“逆位姿绑定矩阵”数组的对应元素处即可完成骨骼动画的关节变换。注意三个变换的顺序不要搞混了,否则变换将是你想象不到的结果。对于我们祖传的D3D左手坐标系来说,连乘的顺序是
S
m
a
t
r
i
x
×
Q
m
a
t
r
i
x
×
T
m
a
t
r
i
x
S_{matrix}\times Q_{matrix} \times T_{matrix}
Smatrix×Qmatrix×Tmatrix,如果你习惯右手的话反过来即可,当然别忘了根据你使用的3D数学库函数的左右手习惯还有可能需要进行转置!
9.3、存储方面的考虑
前一小节已经说了三个基本变换在表示时,用两个表示缩放和位移的3维向量和一个4分量的四元数即可,这时对于一个关节的一个时刻点的帧来说,变换只需要存储
2
×
3
×
s
i
z
e
o
f
(
f
l
o
a
t
)
4
∗
s
i
z
e
o
f
(
f
l
o
a
t
)
=
40
B
y
t
e
s
2 \times 3 \times sizeof(float) + 4 * sizeof(float) = 40 Bytes
2×3×sizeof(float)+4∗sizeof(float)=40Bytes,而如果要存储他们的矩阵形式的话则需要
3
×
4
×
4
×
s
i
z
e
o
f
(
f
l
o
a
t
)
=
192
B
y
t
e
s
3 \times 4 \times 4 \times sizeof(float) = 192Bytes
3×4×4×sizeof(float)=192Bytes,而中间足足节约了152Bytes!
一般的模型文件中,骨骼的数量都在几十个,并且每一个关节的动画序列少的需要几十帧数据,多的则需要成百上千帧的数据,这其中的存储节约将是相当可观的!更有甚者,在一些早期的引擎中,甚至将前述的三个变换需要的向量和四元数“压缩”存储到两个4分量的半精度(half)浮点数的数组中,其中主要就是只用一个变量来表示所有方向上的缩放,因为现实中大多数缩放变换其实在每个轴向上都是大小相同的,所有用一个变量来表示已经足够了,这样一个缩放变量和一个3维的位移向量共同存储在一个4分量的向量中,再加上一个4分量的四元数,并且在牺牲一定精度的情况下将32位float数,用16位的half浮点数表示,此时一个关节的一帧变换只需要
2
×
4
×
s
i
z
e
o
f

网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
r
i
x
S_{matrix}\times Q_{matrix} \times T_{matrix}
Smatrix×Qmatrix×Tmatrix,如果你习惯右手的话反过来即可,当然别忘了根据你使用的3D数学库函数的左右手习惯还有可能需要进行转置!
9.3、存储方面的考虑
前一小节已经说了三个基本变换在表示时,用两个表示缩放和位移的3维向量和一个4分量的四元数即可,这时对于一个关节的一个时刻点的帧来说,变换只需要存储
2
×
3
×
s
i
z
e
o
f
(
f
l
o
a
t
)
4
∗
s
i
z
e
o
f
(
f
l
o
a
t
)
=
40
B
y
t
e
s
2 \times 3 \times sizeof(float) + 4 * sizeof(float) = 40 Bytes
2×3×sizeof(float)+4∗sizeof(float)=40Bytes,而如果要存储他们的矩阵形式的话则需要
3
×
4
×
4
×
s
i
z
e
o
f
(
f
l
o
a
t
)
=
192
B
y
t
e
s
3 \times 4 \times 4 \times sizeof(float) = 192Bytes
3×4×4×sizeof(float)=192Bytes,而中间足足节约了152Bytes!
一般的模型文件中,骨骼的数量都在几十个,并且每一个关节的动画序列少的需要几十帧数据,多的则需要成百上千帧的数据,这其中的存储节约将是相当可观的!更有甚者,在一些早期的引擎中,甚至将前述的三个变换需要的向量和四元数“压缩”存储到两个4分量的半精度(half)浮点数的数组中,其中主要就是只用一个变量来表示所有方向上的缩放,因为现实中大多数缩放变换其实在每个轴向上都是大小相同的,所有用一个变量来表示已经足够了,这样一个缩放变量和一个3维的位移向量共同存储在一个4分量的向量中,再加上一个4分量的四元数,并且在牺牲一定精度的情况下将32位float数,用16位的half浮点数表示,此时一个关节的一帧变换只需要
2
×
4
×
s
i
z
e
o
f
[外链图片转存中…(img-JkuDR24T-1715494364707)]
[外链图片转存中…(img-8mDbzmiL-1715494364707)]
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!






















 906
906











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








