样本相关系数 r X Y = n ∑ X i Y i − ∑ X i ∑ Y i n ∑ X i 2 − ( ∑ X i ) 2 n ∑ Y i 2 − ( ∑ Y i ) 2 \displaystyle r_{XY}=\frac{n\sum X_iY_i - \sum Xi \sum Y_i}{\sqrt{n \sum{X_i}^2 -(\sum X_i)^2}\sqrt{n \sum{Y_i}^2 -(\sum Y_i)^2}} rXY=n∑Xi2−(∑Xi)2 n∑Yi2−(∑Yi)2 n∑XiYi−∑Xi∑Yi
或
r X Y = ∑ ( X i − X ‾ ) ( ( Y i − Y ‾ ) ∑ ( X i − X ‾ ) 2 ∑ ( Y i − Y ‾ ) 2 \displaystyle r_{XY}=\frac{\sum (X_i-\overline{X})((Y_i-\overline{Y})}{\sqrt{\sum{(X_i - \overline{X})}^2 \sum{(Y_i - \overline{Y})}^2}} rXY=∑(Xi−X)2∑(Yi−Y)2 ∑(Xi−X)((Yi−Y)
其中X_i和Y_i分别是变量X和Y的样本观测值, X ‾ \overline{X} X和 Y ‾ \overline{Y} Y分别是变量X和Y的样本观测值的平均值;n为样本的个数,也称样本容量。
这样计算的样本相关系数是总体相关系数的一致估计。
1.1.2.2相关系数特点
- r X Y = r Y X r_{XY}=r_{YX} rXY=rYX
2.相关系数只反映线性相关程度,不能说明非线性相关关系。
3.相关系数不能确定变量的因果关系。
4.样本相关系数是对总体相关系数的估计。
1.1.3回归分析
相关分析不能说明变量间相关关系的具体形式,相关关系表明变量间相关关系的性质和程度。要具体测定变量之间相关关系的具体形式,还要用到回归分析的方法。
回归分析研究的是总体中解释变量与被解释变量之间客观存在的协变规律性。
总体回归函数的条件期望表示方式:
E ( Y ∣ X i ) = f ( X i ) = β 1 + β 2 X i E(Y|X_i)=f(X_i)=β_1+β_2X_i E(Y∣Xi)=f(Xi)=β1+β2Xi β 1 为 截 距 系 数 , β 2 为 斜 率 系 数 β_1为截距系数,β_2为斜率系数 β1为截距系数,β2为斜率系数
条件期望满足此方程式的函数称为总体回归函数(PRF)(population regression function)
μ i = Y i − E ( Y ∣ X i ) μ_i=Y_i-E(Y|X_i) μi=Yi−E(Y∣Xi) 或 Y i = E ( Y ∣ X i ) + μ i Y_i=E(Y|X_i)+μ_i Yi=E(Y∣Xi)+μi
如果函数是线性函数,则有
μ i = Y i − β 1 − β 2 X i μ_i=Y_i-β_1-β_2X_i μi=Yi−β1−β2Xi 或 Y i = β 1 + β 2 X i + μ i Y_i=β_1+β_2X_i+μ_i Yi=β1+β2Xi+μi
随机扰动项 μ i μ_i μi表示那些对Y有影响但是没有纳入模型的诸多因素的综合影响。
对 Y i = E ( Y ∣ X i ) + μ i Y_i=E(Y|X_i)+μ_i Yi=E(Y∣Xi)+μi式子两边同取对X_i的条件期望,则有
E ( Y ∣ X i ) = E E(Y|X_i)=E E(Y∣Xi)=E { E ( Y ∣ X i ) E(Y|X_i) E(Y∣Xi) } + E ( μ i ∣ X i ) = E ( Y ∣ X i ) + E ( μ i ∣ X i ) +E(μ_i|X_i)=E(Y|X_i)+E(μ_i|X_i) +E(μi∣Xi)=E(Y∣Xi)+E(μi∣Xi)
即暗含 E ( Y ∣ X i ) = 0 E(Y|X_i)=0 E(Y∣Xi)=0的假定条件,即回归曲线是通过Y的条件期望或条件均值的。
- 在总体回归函数中引入随机扰动项的原因:
1.作为位置影响因素的代表。
2.作为无法取得数据的已知因素的代表。
3.’作为众多细小影响因素的综合代表。
4.模型设定误差。
5.经济现象的内在随机性。
Y的样本观测值的条件均值解释变量X而变动的轨迹,称为样本回归线
把被解释变量Y的样本条件均值表示为解释变量X的某种函数,称为样本回归函数(SRF)。(Sample regression function)
如果为线性函数:
Y i ^ = β 1 ^ + β 2 ^ X i \hat{Y_i}=\hat{β_1}+\hat{β_2}X_i Yi=β1+β2^Xi
实际观测的被解释变量值 Y i Y_i Yi不完全等于样本条件均值 Y i ^ \hat{Y_i} Yi^,二者之差可以用 e i e_i ei表示。
则: Y i − Y i ^ = e i Y_i -\hat{Y_i}=e_i Yi−Yi^=ei 或 Y i = β 1 ^ + β 2 ^ X i + e i Y_i=\hat{β_1}+\hat{β_2}X_i+e_i Yi=β1+β2Xi+ei
需要明确:样本回归函数与总体回归函数有所区别。总体回归函数虽然未知,但是是确定的:样本回归线随抽样波动而变化,可以有多条。总体回归函数的参数 β 1 和 β 2 β_1和β_2 β1和β2是确定的常数,样本回归函数的参数 β 1 ^ 和 β 2 ^ \hat{β_1}和\hat{β_2} β1和β2是随机变量。SRF与PRF总是会存在差异。
====================================================================================
五个基本假定:
- 1.零均值假定 给定解释变量 X i X_i Xi,随机扰动项 u i u_i ui的条件均值始终为零。
E ( u i ∣ X i ) = 0 E(u_i|X_i)=0 E(ui∣Xi)=0
- 2.同方差假定 对于每个给定的 X i X_i Xi,随机扰动项 u i u_i ui的条件期方差都等于一个常数 σ 2 σ^2 σ2
V a r ( u i ∣ X i ) = E [ u i − E ( u i ∣ X i ) ] 2 = E ( u i 2 ) = σ 2 Var(u_i|X_i)=E[u_i-E(u_i|X_i)]2=E(u_i2)=σ^2 Var(ui∣Xi)=E[ui−E(ui∣Xi)]2=E(ui2)=σ2
- 3.无自相关假定 随机扰动项 u i u_i ui的逐次值互不相关,或者说对于所有的i和j(i≠j), u i 和 u j 的 协 方 差 为 零 。 u_i和u_j的协方差为零。 ui和uj的协方差为零。
C o v ( u i , u j ) = E [ u i − E ( u i ) ] [ u j − E ( u j ) ] = E ( u i u j ) = 0 Cov(u_i,u_j)=E[u_i-E(u_i)][u_j-E(u_j)]=E(u_iu_j)=0 Cov(ui,uj)=E[ui−E(ui)][uj−E(uj)]=E(uiuj)=0
- 4.随机扰动项 u i u_i ui与解释变量 X i X_i Xi不相关,可表示
为 C o v ( u i , X i ) = E [ u i − E ( u i ) ] [ X i − E ( X i ) ] = 0 Cov(u_i,X_i)=E[u_i-E(u_i)][X_i-E(X_i)]=0 Cov(ui,Xi)=E[ui−E(ui)][Xi−E(Xi)]=0
- 5.正态性假定 即假定随机扰动项服从期望为0,方差为 σ 2 σ^2 σ2的正态分布,表示为
u i u_i ui~ N ( 0 , σ 2 ) N(0,σ^2) N(0,σ2)
满足此五个假设的线性回归模型,称为古典线性回归模型(CLRM)
其中四个假定,也可以用 Y i Y_i Yi表示:
对零均值假定有: E ( Y i ∣ X i ) = β 1 + β 2 X i E(Y_i|X_i)=β_1+β_2X_i E(Yi∣Xi)=β1+β2Xi
对同方差假定有: V a r ( Y i ∣ X i ) = σ 2 Var(Y_i|X_i)=σ^2 Var(Yi∣Xi)=σ2
对无自相关假定有: C o v ( Y i , Y j ) = 0 ( i ≠ j ) Cov(Y_i,Y_j)=0(i≠j) Cov(Yi,Yj)=0(i=j)
对正态性假定有: Y Y Y~ N ( β 1 + β 2 X i , σ 2 ) N(β_1+β_2X_i,σ^2) N(β1+β2Xi,σ2)
用产生样本概率最大的原则去确定样本回归函数,称为极大似然准则;
用估计剩余平方和最小的原则确定样本回归函数,称为最小二乘准则。
最小二乘法,也称最小二乘估计(OLS或OLSE)
最小二乘法使样本回归函数尽可能地接近总体回归函数,需满足最小二乘准则,使剩余平方和 Σ e i 2 Σe_i^2 Σei2最小。
即
m i n Σ e i 2 = m i n Σ ( Y i − Y i ^ ) 2 = m i n Σ ( Y i − β 1 ^ − β 2 ^ X i ) 2 minΣe_i2=minΣ(Y_i-\hat{Y_i})2=minΣ(Y_i-\hat{β_1}-\hat{β_2}X_i)^2 minΣei2=minΣ(Yi−Yi)2=minΣ(Yi−β1−β2^Xi)2
…
β 2 ^ = Σ ( X i − X ‾ ) ( Y i − Y ‾ ) Σ ( X i 2 − X ^ ) = x i y i x i 2 \hat{β_2}=\frac{Σ(X_i-\overline{X})(Y_i-\overline{Y})}{Σ(X_i2-\hat{X})}=\frac{x_iy_i}{x_i2} β2=Σ(Xi2−X)Σ(Xi−X)(Yi−Y)=xi2xiyi
β 1 ^ = Y ‾ − β 2 ^ X ‾ \hat{β_1}=\overline{Y}-\hat{β_2}\overline{X} β1=Y−β2X
用普通最小二乘法拟合的样本回归线有以下性质
-
样本回归线通过样本均值。
-
估计值 Y i ^ \hat{Y_i} Yi^的均值 Σ Y i ^ n \frac{Σ\hat{Y_i}}{n} nΣYi^等于实际 Y i Y_i Yi的均值。
-
剩余项 e i e_i ei的均值的为0。
-
被解释变量估计值 Y i ^ \hat{Y_i} Yi^与剩余项 e i e_i ei不相关。
-
解释变量 X i X_i Xi与剩余项 e i e_i ei不相关。
2.4.1 参数估计量的评价标准
选择参数估计量时应考虑以下一些标准:
1.无偏性
如果参数的估计量 β ^ \hat{β} β^的期望等于参数的真实值β,即 E ( β ^ ) = β E(\hat{β})=β E(β^)=β,则称 β ^ \hat{β} β^是参数β的无偏估计量。
如果参数估计量 β ∗ β^* β∗是期望值不等于参数β的真实值,则称 β ∗ β^* β∗是有偏的,其偏倚为 E ( β ∗ ) − β E(β^*)-β E(β∗)−β,也称系统误差。无偏即无系统误差。
计量经济研究中应尽可能寻找符合无偏性要求的参数估计量。
2.有效性
一个估计量若不仅有无偏性,而且具有最小方差性,则称这个估计量为有效估计量。
即对于参数β的无偏估计量 β ^ \hat{\beta} β^,如果对于参数的任意一个无偏估计量 β ∗ \beta^* β∗,都有 V a r ( β ^ ) ≤ V a r ( β ∗ ) Var(\hat{β})≤Var(β^*) Var(β^)≤Var(β∗),则称 β ^ \hat{β} β^是参数β的有效估计量。
或者说, β ^ \hat{β} β^较 β ∗ β^* β∗有效。
3.一致性
样本容量趋于无穷大时,如果估计量, β ^ \hat{β} β^的抽样分布依概率收敛于总体参数真实值β,即
P lim n → ∞ β ^ = β P \displaystyle \lim_{n \rightarrow \infty} \hat{\beta}=β Pn→∞limβ^=β
或 lim n → ∞ P [ ( ∣ β ^ − β ∣ ) < ε ] = 1 \displaystyle \lim_{n \rightarrow \infty}P[(|\hatβ-β|)<ε]=1 n→∞limP[(∣β^−β∣)<ε]=1
也就是说,当样本容量n→∞时,估计量 β ^ \hat{β} β^与总体参数真实值β的距离 β ^ − β \hat{β}-β β^−β的绝对值小于任意给定正数ε的概率等于1,则称估计量 β ^ \hat{β} β^为一致估计量。
(也称相合性,相合估计量)
2.4.2OLS估计量的统计特性
在古典假定完全满足的情况下,回归模型参数的最小二乘估计量具有以下统计性质。
1.线性特性
由 β 2 ^ = x i y i x i 2 \hat{β_2}=\frac{x_iy_i}{x_i^2} β2^=xi2xiyi,详细过程略
可以有 β 2 ^ = Σ k i Y i \hat{β_2}=Σk_iY_i β2^=ΣkiYi,其中 k i k_i ki是一组常数,所以 β 2 ^ \hat{β_2} β2^是 Y i Y_i Yi的线性相关函数。
类似也有, β 1 ^ \hat{β_1} β1^是 Y i Y_i Yi的线性相关函数。
2.无偏性
E ( β 2 ^ ) = β 2 E(\hat{β_2})=β_2 E(β2^)=β2
E ( β 1 ^ ) = β 1 E(\hat{β_1})=β_1 E(β1^)=β1
这表明最小二乘法估计的参数 β 1 β_1 β1和 β 2 β_2 β2的期望值等于总体回归函数参数的真实值 β 1 β_1 β1和 β 2 β_2 β2,所以OLS估计式是无偏估计量。
3.有效性
普通最小二乘估计 β 1 ^ \hat{β_1} β1^和 β 2 ^ \hat{β_2} β2^具有最小的方差。证明过程略。
也可以用标准误差度量估计量的精确性,标准误差(standard error)是方差的平方根,可以用SE表示。
V a r ( β 2 ^ ) = σ 2 Σ x i 2 Var(\hat{β_2})=\frac{σ2}{Σx_i2} Var(β2^)=Σxi2σ2
V a r ( β 1 ^ ) = σ 2 ∑ X i 2 n ∑ x i 2 Var(\hat{β_1})=σ^2 \frac{\sum{X_i^2}}{n \sum{x_i^2}} Var(β1^)=σ2n∑xi2∑Xi2
S E ( β 2 ^ ) = σ ∑ x i 2 SE(\hat{β_2})=\frac{σ}{\sqrt{\sum x_i^2}} SE(β2^)=∑xi2 σ
S E ( β 1 ^ ) = σ ∑ X i 2 n ∑ x i 2 SE(\hat{β_1})=σ \sqrt{\frac{\sum X_i^2}{n \sum x_i^2}} SE(β1^)=σn∑xi2∑Xi2
其中 σ 2 σ^2 σ2作为总体随机扰动项 u i u_i ui的方差是未知的,也需要通过样本估计。
用 σ 2 ^ = ∑ e i 2 n − 2 \hat{σ^2}=\frac{\sum e_i^2}{n-2} σ2^=n−2∑ei2计算的 σ 2 σ^2 σ2的估计值 σ 2 ^ \hat{σ^2} σ2^是对 σ 2 σ^2 σ2的无偏估计。
e i 2 e_i^2 ei2是剩余平方和;n-2是自由度。
综上,OLS估计量 β 1 ^ \hat{β_1} β1^和 β 2 ^ \hat{β_2} β2^是总体参数 β 1 β_1 β1和 β 2 β_2 β2的最佳线性无偏估计量。(Best linear unbiased estimator,BLUE)。这个结论也称高斯-马尔可夫定理。
==============================================================================
所估计样本回归线对样本观测数据拟合的优劣程度,称为样本回归线的拟合优度。
-
被解释变量Y的样本观测值与其平均值的离差平方和 ∑ ( Y i − Y ‾ ) 2 = ∑ y i 2 \sum{(Y_i-\overline{Y})2}=\sum{y_i2} ∑(Yi−Y)2=∑yi2,称为总变差或总离差平方和(total sum of squares)。用TSS表示。
-
被解释变量Y的样本估计值与其平均值的离差平方和 ∑ ( Y i ^ − Y ‾ ) 2 = ∑ y i ^ 2 \sum{(\hat{Y_i}-\overline{Y})}2=\sum{\hat{y_i}2} ∑(Yi−Y)2=∑yi2,称为回归解释平方和。是由模型回归线作出解释的变差,用ESS表示。
-
被解释变量观测值与估计值之间的平方和 ∑ ( Y i − Y i ^ ) 2 = ∑ e i 2 \sum{(Y_i-\hat{Y_i})}^2= \sum{e_i^2} ∑(Yi−Yi^)2=∑ei2,是回归线未作出解释的平方和,称为残差平方和(residualc sum of squares),用RSS*表示。(未解释平方和)
三者关系:
TSS=ESS+RSS
∑ ( Y i − Y ‾ ) 2 = ∑ ( Y i ^ − Y ‾ ) 2 + ∑ ( Y i − Y i ^ ) 2 \sum{(Y_i-\overline{Y})}2=\sum{(\hat{Y_i}-\overline{Y})}2+\sum{(Y_i-\hat{Y_i})}^2 ∑(Yi−Y)2=∑(Yi−Y)2+∑(Yi−Yi)2
∑ y i 2 = ∑ y i ^ 2 + ∑ e i 2 \sum{y_i2}=\sum{\hat{y_i}2}+\sum{e_i^2} ∑yi2=∑yi^2+∑ei2
TSS=ESS+RSS
1 = E S S T S S + R S S T S S = 解 释 平 方 和 的 权 重 + 未 解 释 平 方 和 的 权 重 1 = \frac{ESS}{TSS}+\frac{RSS}{TSS}=解释平方和的权重+未解释平方和的权重 1=TSSESS+TSSRSS=解释平方和的权重+未解释平方和的权重
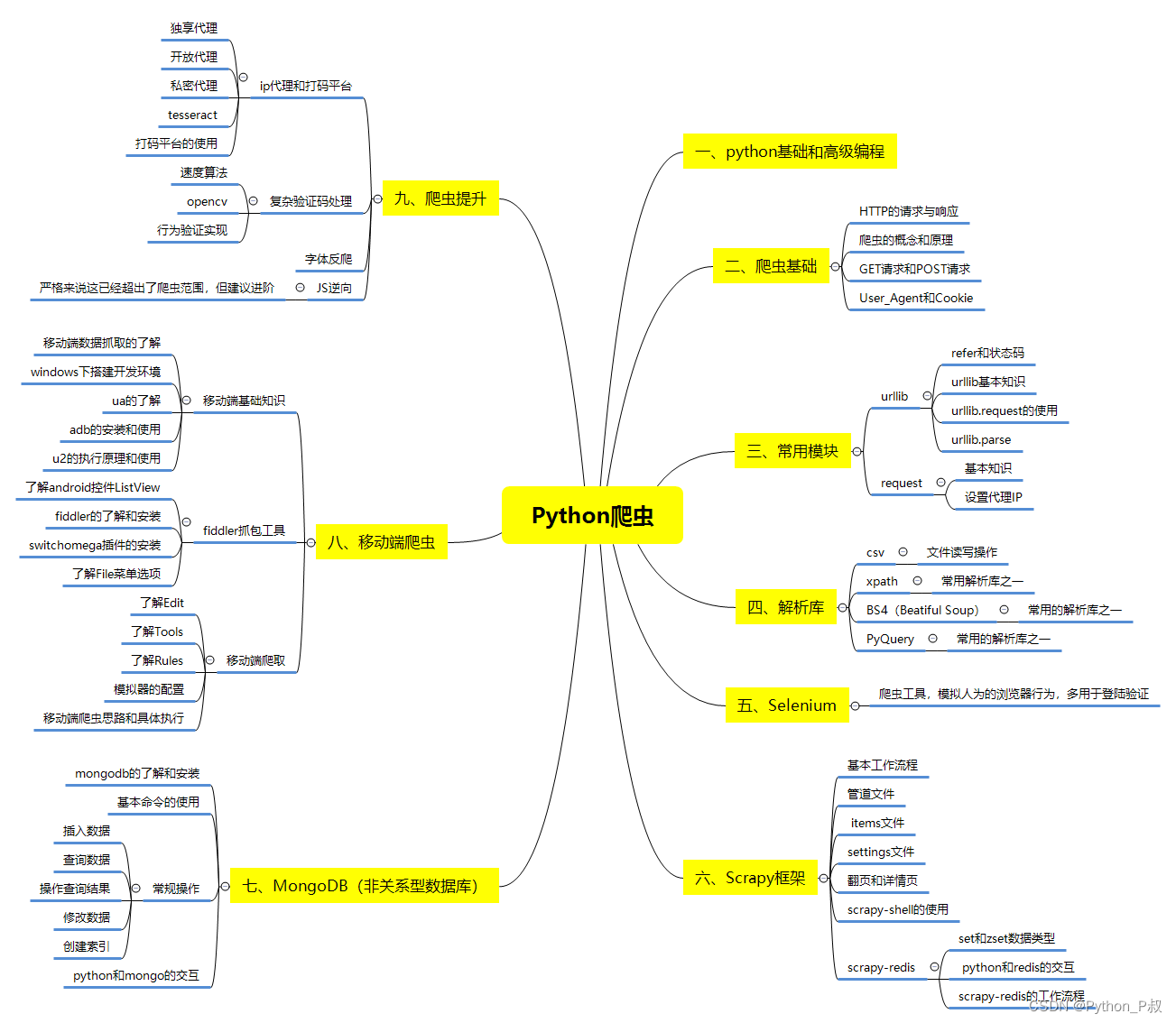
一、Python所有方向的学习路线
Python所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照下面的知识点去找对应的学习资源,保证自己学得较为全面。
二、Python必备开发工具
工具都帮大家整理好了,安装就可直接上手!
三、最新Python学习笔记
当我学到一定基础,有自己的理解能力的时候,会去阅读一些前辈整理的书籍或者手写的笔记资料,这些笔记详细记载了他们对一些技术点的理解,这些理解是比较独到,可以学到不一样的思路。
四、Python视频合集
观看全面零基础学习视频,看视频学习是最快捷也是最有效果的方式,跟着视频中老师的思路,从基础到深入,还是很容易入门的。
五、实战案例
纸上得来终觉浅,要学会跟着视频一起敲,要动手实操,才能将自己的所学运用到实际当中去,这时候可以搞点实战案例来学习。
六、面试宝典
简历模板
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!






















 766
766











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








