信号的抽样与恢复
目录
一、 目的
(1) 验证抽样定理;
(2) 熟悉信号的抽样与恢复过程;
(3) 通过实验观察欠采样时信号频谱的混迭现象;
(4) 掌握采样前后信号频谱的变化, 加深对采样定理的理解;
(5) 掌握采样频率的确定方法。
二、 内容和原理
信号的抽样与恢复示意图如图 5.1 所示。

图 5-1 信号的抽样与恢复示意图
抽样定理指出: 一个有限频宽的连续时间信号f (t),其最高频率为![]() m ,经过等间 隔抽样后,只要抽样频率
m ,经过等间 隔抽样后,只要抽样频率![]() s 不小于信号最高频率
s 不小于信号最高频率![]() m 的二倍,即满足
m 的二倍,即满足![]() s ≥ 2
s ≥ 2![]() m ,就能从 抽样信号fs (t) 中恢复原信号,得到f0 (t) 。f 0 (t) 与f (t) 相比没有失真,只有幅度和相位
m ,就能从 抽样信号fs (t) 中恢复原信号,得到f0 (t) 。f 0 (t) 与f (t) 相比没有失真,只有幅度和相位

由原理框图不难看出,A/D 转换环节实现抽样、量化、编码过程;数字信号处理环节对 得到的数字信号进行必要的处理; D/A 转换环节实现数/模转换,得到连续时间信号;低通滤波器的作用是滤除截止频率以外的信号,恢复出与原信号相比无失真的信号f 0 (t) 。
三、涉及的 MATLAB 函数
subplot(2,1,1)
xlabel('时间, msec');ylabel('幅值'); title('连续时间信号 x_{a}(t)');
axis([0 1 -1.2 1.2]) stem(k,xs);grid;
linspace(-0.5,1.5,500)'; ones(size(n)
freqs(2,[1 2 1],wa);
plot(wa/(2*pi),abs(ha)
buttord(Wp, Ws, 0.5, 30,'s'); [Yz, w] = freqz(y, 1, 512);
M= input('欠采样因子 = ');
length(nn1)
y = interp(x,L)
[b,a] = butter(N, Wn, 's'); get(gfp,'units');
set(gfp,'position',[100 100 400 300]); fx1=fft(xs1)
abs(fx2(n2+1))
y = resample(x,L,M);
四、内容与方法
1. 验证性作业
1) 余弦信号的采样 MATLAB 程序:
clf;
% 连续时间信号
t = -1:0.0005:1; % 时间范围,包括负值
xa = sin(2*pi*13*t)./(t + (t==0)); % sin(t)/t,处理t=0的情况
subplot(2,1,1);
plot(t, xa); grid;
xlabel('时间, 秒'); % 修改为秒
ylabel('幅值');
title('连续时间信号 x_{a}(t) = \frac{\sin(2\pi f t)}{t}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围以显示负半轴
% 离散时间信号
T = 0.1; % 采样间隔
n = -1:T:1; % 离散时间点,包括负值
xs = sin(2*pi*13*n)./(n + (n==0)); % sin(t)/t,处理n=0的情况
k = 0:length(n)-1; % 离散时间索引
subplot(2,1,2);
stem(n, xs, 'r', 'filled'); % 使用n作为x轴
grid;
xlabel('时间, 秒'); % 修改为秒
ylabel('幅值');
title('离散时间信号 x[n] = \frac{\sin(2\pi f n)}{n}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围以显示负半轴余弦信号的采样结果如图 5.3 所示。
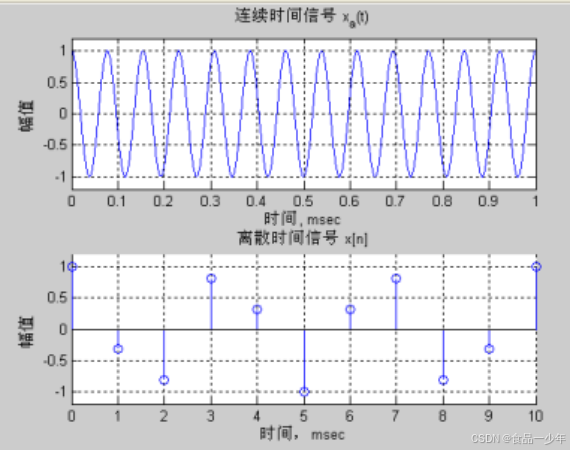
图 5-3 余弦信号的采样
2)采样与重构 MATLAB 程序:
clf;
T = 0.1;f = 13;
n = (0:T:1)';
xs = cos(2*pi*f*n);
t = linspace(-0.5,1.5,500)';
ya = sinc((1/T)*t(:,ones(size(n))) - (1/T)*n(:,ones(size(t)))')*xs; plot(n,xs,'o',t,ya);grid;
xlabel('时间, msec');ylabel('幅值'); title('重构连续信号 y_{a}(t)');
axis([0 1 -1.2 1.2]);余弦信号的采样与重构结果如图 5.4 所示。

图 5-4 正弦信号的采样与重构结果
2. 程序设计作业
设计一模拟信号:x(t)=3sin(2π·f·t) 。采样频率为 5120Hz,取信号频率 f=150Hz(正常采 样)和 f=3000Hz(欠采样)两种情况进行采样分析。
实验程序:
clf;
t = 0:0.0000005:0.02;
f1= 150; f2=3000;
xa1= 3*sin(2*pi*f1*t); xa2= 3*sin(2*pi*f2*t); fs=5120;
T = 1/fs;
nn1= -1:T:1; nn2= -1:T:1;
xs1=3*sin(2*pi*f1*nn1); xs2=3*sin(2*pi*f2*nn2); k1= 0:length(nn1)-1;
k2= 0:length(nn2)-1;
subplot(3,2,1) plot(t,xa1);grid
xlabel('时间, msec');ylabel('幅值'); title('连续时间信号 x_{a1}(t)');
axis([0 0.02 -3 3])
subplot(3,2,2) plot(t,xa2);grid
xlabel('时间, msec');ylabel('幅值'); title('连续时间信号 x_{a2}(t)');
axis([0 0.001 -3 3]) subplot(3,2,3);
stem(k1,xs1);grid;
xlabel('时间, msec');ylabel('幅值'); title('离散时间信号 x1[n]');
axis([0 100 -3 3]) subplot(3,2,4);
stem(k2,xs2);grid;
xlabel('时间, msec');ylabel('幅值'); title('离散时间信号 x2[n]');
axis([0 5 -3 3]) subplot(3,2,5)
N1=length(xs1); fx1=fft(xs1);
df1=fs/N1; n1=0:N1/2; f1=n1*df1;
plot(f1,abs(fx1(n1+1))*2/N1); grid;
set(gca,'XTickMode','manual','XTick',[0,50,100,150,200,250,300]) set(gca,'YTickMode','manual','YTick',[1,2,3,4])
title('离散时间信号 x1[n]和频谱图'); axis([0 300 0 4])
subplot(3,2,6)
N2=length(xs2); fx2=fft(xs2);
df2=fs/N2; n2=0:N2/2; f2=n2*df2;
plot(f2,abs(fx2(n2+1))*2/N2); grid;
set(gca,'XTickMode','manual','XTick',[100,500,1000,1500,2120,2500]) set(gca,'YTickMode','manual','YTick',[1,2,3,4])
title('离散时间信号 x2[n]和频谱图'); 执行后得到如图 5.14:

图 5-14 两种信号的采样及频谱图
从图 5.14 中我们可以看出,当正常采样时,频谱图上和原信号频谱一样.
方波抽样
MATLAB 程序:
% MATLAB 示例:混迭现象的演示
clc;
clear;
%% 参数设置
f_signal = 200; % 方波的基频,200 Hz
fs_sample = 500; % 采样频率,500 Hz(小于基频谐波采样要求)
t_duration = 0.05; % 信号持续时间,0.05 秒
t_high_res = 1e-6; % 高分辨率时间步长,用于生成原始信号
%% 生成方波信号
t_orig = 0:t_high_res:t_duration; % 原始时间轴(高分辨率)
signal = square(2 * pi * f_signal * t_orig); % 方波信号
% 绘制原始方波信号
figure;
subplot(3, 1, 1);
plot(t_orig, signal, 'b');
title('原始方波信号');
xlabel('时间 (s)');
ylabel('幅值');
xlim([0, 0.01]); % 放大查看一个周期
grid on;
%% 对信号进行采样
t_sample = 0:1/fs_sample:t_duration; % 采样时间轴
sampled_signal = square(2 * pi * f_signal * t_sample); % 采样后的信号
% 绘制采样信号
subplot(3, 1, 2);
stem(t_sample, sampled_signal, 'r', 'MarkerFaceColor', 'r');
title('采样后的方波信号');
xlabel('时间 (s)');
ylabel('幅值');
xlim([0, 0.01]); % 放大查看一个周期
grid on;
%% 频谱分析
% 原始信号的频谱
N_orig = length(t_orig); % FFT 点数
freq_orig = linspace(0, 1/(2*t_high_res), N_orig/2); % 频率轴
fft_orig = abs(fft(signal)); % 原始信号 FFT
fft_orig = fft_orig(1:N_orig/2); % 取一半频率(正频率部分)
% 采样信号的频谱
N_sample = length(t_sample); % FFT 点数
freq_sample = linspace(0, fs_sample/2, N_sample/2); % 频率轴
fft_sample = abs(fft(sampled_signal)); % 采样信号 FFT
fft_sample = fft_sample(1:N_sample/2); % 取一半频率(正频率部分)
% 绘制频谱
subplot(3, 1, 3);
plot(freq_orig, fft_orig, 'b'); hold on;
stem(freq_sample, fft_sample, 'r', 'MarkerFaceColor', 'r');
title('频谱对比(蓝色:原始信号,红色:采样信号)');
xlabel('频率 (Hz)');
ylabel('幅值');
legend('原始信号频谱', '采样信号频谱');
grid on;
%% 观察混迭现象
fprintf('采样频率 fs = %d Hz,原始信号基频 f = %d Hz\n', fs_sample, f_signal);
fprintf('混迭现象产生的频率折叠:\n');
fprintf('- 第1谐波(600 Hz)混迭到 %d Hz\n', abs(600 - fs_sample)); % 混迭频率
fprintf('- 第2谐波(1000 Hz)混迭到 %d Hz\n', abs(1000 - 2*fs_sample)); % 混迭频率

高斯函数抽样
MATLAB 程序:
clf; % 清除当前图形窗口
% 连续时间高斯信号
t = -1:0.0005:1; % 时间向量,从-1到1,步长为0.0005
mu = 0; % 高斯函数的均值
sigma = 0.1; % 高斯函数的标准差
xg = exp(-((t-mu).^2)/(2*sigma^2)); % 高斯函数
% 绘制连续时间高斯信号
subplot(2,1,1)
plot(t, xg);
grid on;
xlabel('时间, msec');
ylabel('幅值');
title('连续时间信号 x_g(t)');
axis([-1 1 min(xg) max(xg)]);
% 离散时间高斯信号
T = 0.1; % 采样周期
n = -1:T:1; % 离散时间向量,从-1到1,步长为0.1
xgd = exp(-((n-mu).^2)/(2*sigma^2)); % 离散时间高斯函数
k = 0:length(n)-1; % 离散时间索引
% 绘制离散时间高斯信号
subplot(2,1,2)
stem(k, xgd);
grid on;
xlabel('时间,msec');
ylabel('幅值');
title('离散时间信号 x_g[n]');
axis([-1 (length(n)-1)*T min(xgd) max(xgd)]); % 调整坐标轴范围以适应数据
抽样信号抽样
clf;
% 连续时间信号
t = -1:0.0005:1; % 时间范围,包括负值
xa = sin(2*pi*13*t)./(t + (t==0)); % sin(t)/t,处理t=0的情况
subplot(2,1,1);
plot(t, xa); grid;
xlabel('时间, 秒'); % 修改为秒
ylabel('幅值');
title('连续时间信号 x_{a}(t) = \frac{\sin(2\pi f t)}{t}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围以显示负半轴
% 离散时间信号
T = 0.1; % 采样间隔
n = -1:T:1; % 离散时间点,包括负值
xs = sin(2*pi*13*n)./(n + (n==0)); % sin(t)/t,处理n=0的情况
k = 0:length(n)-1; % 离散时间索引
subplot(2,1,2);
stem(n, xs, 'r', 'filled'); % 使用n作为x轴
grid;
xlabel('时间, 秒'); % 修改为秒
ylabel('幅值');
title('离散时间信号 x[n] = \frac{\sin(2\pi f n)}{n}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围以显示负半轴
采样与重构
clf;
close all;
% 参数设置
f = 13; % 信号频率
fs_continuous = 2000; % 连续信号的采样频率
T = 0.1; % 离散信号的采样间隔
n_samples = 100; % 离散信号样本数量
% 连续时间信号
t_continuous = -1:1/fs_continuous:1; % 连续时间向量
xa = sin(2*pi*f*t_continuous)./(t_continuous + (t_continuous==0)); % sin(t)/t,处理t=0的情况
subplot(3,1,1);
plot(t_continuous, xa, 'b'); grid;
xlabel('时间, 秒');
ylabel('幅值');
title('连续时间信号 x_{a}(t) = \frac{\sin(2\pi f t)}{t}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围
% 离散时间信号
n = -1:T:1; % 离散时间点,包括负值
xs = sin(2*pi*f*n)./(n + (n==0)); % sin(t)/t,处理n=0的情况
% 绘制离散时间信号
subplot(3,1,2);
stem(n, xs, 'r', 'filled'); % 使用n作为x轴
grid;
xlabel('时间, 秒');
ylabel('幅值');
title('离散时间信号 x[n] = \frac{\sin(2\pi f n)}{n}');
axis([-1 1 -0.5 1.5]); % 调整y轴范围
% 重构信号
% 使用线性插值法重构信号
t_reconstruct = linspace(-1, 1, 1000); % 重构时间点
xs_interpolated = interp1(n, xs, t_reconstruct, 'linear', 'extrap'); % 进行线性插值
% 绘制重构的信号
subplot(3,1,3);
plot(t_reconstruct, xs_interpolated, 'm', 'LineWidth', 1.5); grid;
xlabel('时间, 秒');
ylabel('幅值');
title('重构信号 \hat{x}(t)');
axis([-1 1 -0.5 1.5]); % 调整y轴范围
legend('重构信号');
% 强调原始信号与重构信号的比较
hold on;
plot(t_continuous, xa, 'b--', 'LineWidth', 1);
hold off;
% 添加图例
legend('重构信号', '连续信号 x_{a}(t)');
五、大作业报告要求
简述目的及原理,按实验步骤附上相应的用 matlab 做出的信号波形和频谱曲线(截图 即可),说明采样频率变化对信号时域和频域特性的影响, 总结实验得出的主要结论。
采样频率过低:
时域特性:当采样频率过低时,信号的时域波形会失真。具体来说,信号的高频成分可能会丢失或被错误地表示,导致信号波形变得粗糙或不连续。示例:如果一个频率为 1000Hz 的正弦波信号被以 1500Hz 的采样频率采样,时域波形会显示出明显的失真和不连续性。
适当的采样频率:
时域特性:当采样频率适当(即大于信号频率的两倍)时,信号的时域波形会比较准确地反映原始信号的形状。信号的高频成分和低频成分都能被正确采样。示例:如果一个频率为 1000Hz 的正弦波信号被以 2500Hz 的采样频率采样,时域波形会非常接近原始信号的波形。
采样频率过高:
时域特性:当采样频率过高时,信号的时域波形会非常平滑,几乎完全复原原始信号的波形。然而,过高的采样频率会增加数据处理的负担和存储需求。示例:如果一个频率为 1000Hz 的正弦波信号被以 10000Hz 的采样频率采样,时域波形会非常平滑,几乎完全复原原始信号。
采样频率变化对信号频域特性的影响
采样频率过低:频域特性:当采样频率过低时,信号的频域特性会受到严重影响。高频成分会被错误地表示为低频成分,从而产生混迭现象。频谱中会出现不属于原始信号的频率成分。示例:如果一个频率为 1000Hz 的正弦波信号被以 1500Hz 的采样频率采样,频谱中会出现 500Hz 的混迭频率。
适当的采样频率:
频域特性:当采样频率适当时,信号的频域特性会比较准确地反映原始信号的频谱。信号的高频成分和低频成分都能被正确采样,频谱中不会出现混迭现象。示例:如果一个频率为 1000Hz 的正弦波信号被以 2500Hz 的采样频率采样,频谱中会准确显示 1000Hz 的频率成分。
采样频率过高:
频域特性:当采样频率过高时,信号的频域特性会非常准确地反映原始信号的频谱。频谱中不会出现混迭现象,但过高的采样频率会增加计算和存储的负担。示例:如果一个频率为 1000Hz 的正弦波信号被以 10000Hz 的采样频率采样,频谱中会准确显示 1000Hz 的频率成分。
实验总结:
奈奎斯特定理的重要性:信号的采样频率必须至少是其最高频率成分的两倍,以避免混叠现象的发生。
采样频率与信号的准确性:较高的采样频率可以提高信号的重构精度和频域分析的准确性,但也增加了计算和存储的要求。较低的采样频率可能导致信号失真,难以提取有用信息。
时频特性的平衡:选择合适的采样频率是时域和频域特性之间的权衡,需根据具体应用需求来设定,以便在保持信号质量的同时优化存储和计算资源。
实验观察中的混叠现象:通过对200 Hz方波信号的采样实验,验证了混叠现象的实际影响,展示了高于奈奎斯特频率的成分如何在采样后错误地表现为低频信号。
正弦函数抽样



六、思考题
(1)x(t) 若信号频率为 5000Hz,请问本实验中的模拟信号采样后的混迭频率是多少 Hz? 分析一 200Hz 的方波信号,采样频率=500Hz,用谱分析功能观察其频谱中的混迭现象。为什 么会产生混迭?


产生混叠的原因:

Matlab代码:
% 参数设置
fs = 500; % 采样频率500Hz
f_signal = 200; % 信号频率200Hz
t = 0:1/fs:1-1/fs; % 时间向量,从0到1秒,减去1/fs以避免混叠
% 生成200Hz方波信号
x = square(2*pi*f_signal*t);
% 绘制连续时间方波信号
subplot(2,1,1);
plot(t, x);
xlabel('时间, sec');
ylabel('幅值');
title('连续时间方波信号 x(t)');
axis([0 1 -1.5 1.5]); % 设置坐标轴范围
% 计算并绘制频谱图
N = length(x);
fx = fft(x);
df = fs/N; % 频率分辨率
f = (0:N-1)*df; % 频率向量
% 由于频谱是对称的,我们只需要显示一半的频谱
half_N = N/2;
subplot(2,1,2);
plot(f(1:half_N), 2*abs(fx(1:half_N))/N);
xlabel('频率, Hz');
ylabel('幅值');
title('方波信号的频谱图');
axis([0 fs/2 0 max(2*abs(fx(1:half_N))/N)]); % 设置坐标轴范围
grid on;
学校的一个大作业比较好玩(ps:想要分高最好彩印,别问我为什么知道)
还有一个音频抽样和一个零极点图绘制的报告感觉这两都比较简单故而没放。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








