大模型系列：SwiGLU激活函数与GLU门控线性单元原理解析

最新推荐文章于 2025-03-12 17:27:08 发布

小城哇哇

最新推荐文章于 2025-03-12 17:27:08 发布

阅读量3k

点赞数 11

文章标签：语言模型学习深度学习 ai 机器学习人工智能

本文链接：https://blog.csdn.net/2401_85325397/article/details/139306896

版权

前言

SwiGLU激活函数在PaLM，LLaMA等大模型中有广泛应用，在大部分测评中相较于Transformer FFN中所使用的ReLU函数都有提升。本篇先介绍LLaMA中SwiGLU的实现形式，再追溯到GLU门控线性单元，以及介绍GLU的变种，Swish激活函数等内容。

内容摘要

LLaMA中SwiGLU的实现形式
GLU门控线性单元原理简述
通过GLU的变种改进Transformer
Swish和SiLU激活函数

LLaMA中SwiGLU的实现形式

SwiGLU本质上是对Transformer的FFN前馈传播层的第一层全连接和ReLU进行了替换，在原生的FFN中采用两层全连接，第一层升维，第二层降维回归到输入维度，两层之间使用ReLE激活函数，计算流程图如下（省略LayerNorm模块）

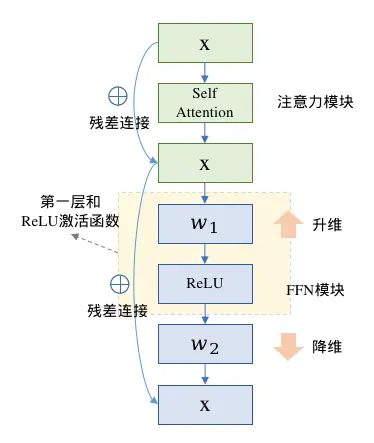
SwiGLU也是全连接配合激活函数的形式，不同的是SwiGLU采用两个权重矩阵和输入分别变换，再配合Swish激活函数做哈达马积的操作，因为FFN本身还有第二层全连接，所以带有SwiGLU激活函数的FFN模块一共有三个权重矩阵，用公式表达如下

其中W1，V为SwiGLU模块的两个权重矩阵，W2为原始FFN的第二层全连接权重矩阵，⊗代表哈达玛积逐位相乘，Swish为激活函数，其中β为Swish激活函数的一个参数，一般β=1此时等同于SiLU激活函数，可视化计算流程图如下

在HuggingFace LLaMA的源码实现中，在Decoder模块LlamaDecoderLayer中的LlamaMLP引入SwiGLU改造了FFN层，实现如下

class LlamaDecoderLayer(nn.Module):
    def __init__(self, config: LlamaConfig):
        ...
        # TODO 门控线性单元
        self.mlp = LlamaMLP(
            hidden_size=self.hidden_size,
            intermediate_size=config.intermediate_size,  # 11008
            hidden_act=config.hidden_act,  # silu
        )

LlamaMLP的实现了SwiGLU逻辑，代码和公式完全对应

class LlamaMLP(nn.Module):
    def __init__(
        self,
        hidden_size: int,  # 4096
        intermediate_size: int,  # 11008
        hidden_act: str,  # silu
    ):
        super().__init__()
        self.gate_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        self.down_proj = nn.Linear(intermediate_size, hidden_size, bias=False)
        self.up_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        self.act_fn = ACT2FN[hidden_act]

    def forward(self, x):
        return self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))

在LLaMA2-7B中，FFN的原始输入维度为4096，一般而言中间层是输入维度的4倍等于16384，由于SwiGLU的原因FFN从2个矩阵变成3个矩阵，为了使得模型的参数量大体保持不变，中间层维度做了缩减，缩减为原来的2/3即10922，进一步为了使得中间层是256的整数倍，有做了取模再还原的操作，最终中间层维度为11008，计算公式如下

GLU门控线性单元原理简述

SwiGLU是GLU门控线性单元的变种，了解SwiGLU必须从GLU入手，GLU提出于2016年发表的论文《nguage modeling with gated convolutional networks》中，GLU是一种类似LSTM带有门机制的网络结构，同时它类似Transformer一样具有可堆叠性和残差连接，它的作用是完成对输入文本的表征，通过门机制控制信息通过的比例，来让模型自适应地选择哪些单词和特征对预测下一个词有帮助，通过堆叠来挖掘高阶语义，通过残差连接来缓解堆叠的梯度消失和爆炸。
堆叠的每一层就是门控GLU门控线性单元，通过Sigmoid激活函数和哈达玛积实现门控机制，公式如下

其中W和V两个卷积操作，当卷积patch size=1时等同于两个全连接层，GLU对输入文本的计算流程示意图如下

相比于LSTM，GLU不需要复杂的门机制，不需要遗忘门，仅有一个输入门，因此计算更加高效，同时作者提出在他的实验中，基于GLU的GCNN门控卷积神经网络和LSTM相比，在相同参数数量和训练环境下，GCNN的预测困惑度更低，表现优于LSTM。

通过GLU的变种改进Transformer

2017年随着Transformer的提出和成功，促进了后续对Transformer结构的改进的研究，比如在2020年发表的论文《GLU Variants Improve Transformer》中，提出使用GLU的变种来改进Transformer的FFN层，作者提出的变种就是将GLU中原始的Sigmoid激活函数替换为其他的激活函数，作者列举了替换为ReLU，GELU和SwiGLU的三种变体，公式如下

本质上就是将Sigmoid激活函数替换为其他激活函数，命名上将激活函数的缩写加在GLU前面作为前缀。进一步作者将这种GLU变体替换FFN中的第一层全连接和激活函数，并且去除了GLU中偏置项bias，以SwiGLU为例，结合FFN它的计算公式为

由于这种方式使得FFN中的权重矩阵从2变为了3，为了使得模型的参数大体不变，因此中间层的向量维度需要削减为原始维度的三分之二。
在论文的实验模块，作者通过数据证明通过GLU变体改造后的Transformer在大多数NLP任务上都比FFN的评价得分明显更高，其中ReGLU在实验中获得了最高的平均分，其次是SwiGLU。

Swish和SiLU激活函数

Swish激活函数由Google团队在2017年提出，被证明在更深的模型上表现出比ReLU更好的性能，Swish的公式如下

其中σ为激活函数Sigmoid，β为Swish的一个参数，通常为一个常数或者让模型自适应学习得到。输入x和Sigmoid相乘使得它类似LSTM中的门机制，因此Swish也被成为self-gated激活函数，只需要一个标量输入即可完成门控操作。
当β=0时，Swish退化为一个线性函数，当β趋近于无穷大时，Swish就变成了ReLU，不同β下Swish的图形如下

Swish函数的曲线是平滑的，并且函数在所有点上都是可微的。这在模型优化过程中很有帮助，被认为是 swish 优于 ReLU 的原因之一。在LLaMA中采用常数β=1，此时Swish也叫SiLU激活函数。
全文完毕。

如何学习大模型AI

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

小编自己也在一线互联网工作十余年了，意识到有很多经验和知识值得分享给大家，也可以通过我的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。

但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

一、大模型全套的学习路线

学习大型人工智能模型，如GPT-3、BERT或任何其他先进的神经网络模型，需要系统的方法和持续的努力。既然要系统的学习大模型，那么学习路线是必不可少的，下面的这份路线能帮助你快速梳理知识，形成自己的体系。

L1级别:AI大模型时代的华丽登场

L2级别：AI大模型API应用开发工程

L3级别：大模型应用架构进阶实践

L4级别：大模型微调与私有化部署

一般掌握到第四个级别，市场上大多数岗位都是可以胜任，但要还不是天花板，天花板级别要求更加严格，对于算法和实战是非常苛刻的。建议普通人掌握到L4级别即可。

二、640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

三、大模型经典PDF籍

随着人工智能技术的飞速发展，AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型，如GPT-3、BERT、XLNet等，以其强大的语言理解和生成能力，正在改变我们对人工智能的认识。那以下这些PDF籍就是非常不错的学习资源。

四、AI大模型商业化落地方案

这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】