PID算法

概述

• PID是比例 列（Proportional）、积分（Integral）、微分(Differential)的缩写
• PID是一种闭环控制算法，它动态改变施加到被控对象的输出值（Out），使得被控对象某一物理量的实际值（Actual），能够快速、准确、稳定地跟踪到指定的目标值 (Target)PID的任务是使误差始终为0

开环和闭环

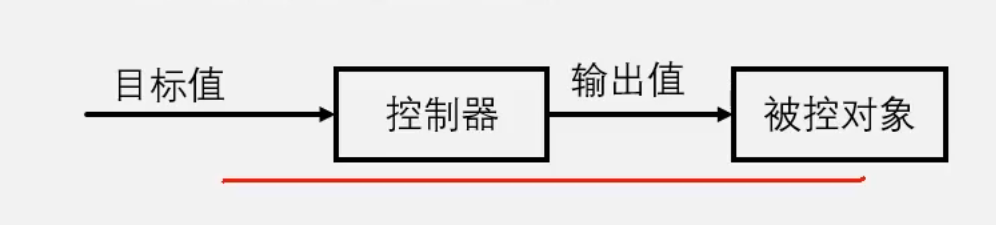
• 开环（OpenLoop）：控制器单向输出值给被控对象，不获取被控对象的反馈，控制器对被控对象的执行状态不清楚
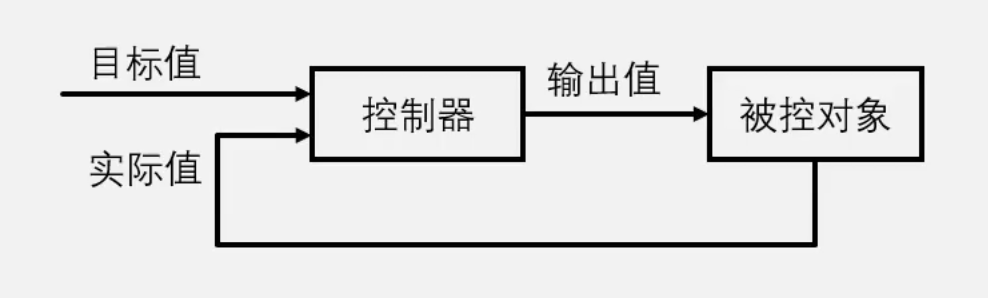
• 闭环（Closed Loop）：控制器输出值给被控对象，同时获取被控对象的反馈控制器知道被控对象的执行状态，可以根据反馈修改输出值以优化控制

各项具体解释

比例项P

• 只含有比例项的PID输出值：
  $out(t)=K_p\ast error(t)$ (error=目标值减实际值）
• 比例项的输出值仅取决于当前时刻的误差，与历史时刻无关。当前存在误差时，比例项输出一个与误差呈正比的值，当前不存在误差时，比例项输出0
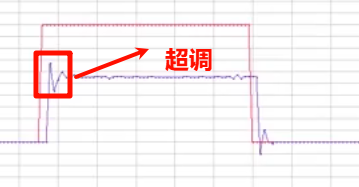
• $K_p$越大，比例项权重越大，系统响应越快，但超调也会随之增加
• 纯比例项控制时，系统一般会存在稳态误差，$K_p$越大，稳态误差越小

稳态误差

• PID稳态误差：系统进入稳态时，实际值和目标值始终存在一个稳定的差值
• 稳态误差产生原因：纯比例项控制时，若误差为0，则比例项结果也为0。被控对象输入0时，一般会自发地向一个方向偏移，产生误差。产生误差后，误差非0，比例项负反馈调控输出，当调控输出力度和自发偏移力度相同时，系统达到稳态
• 判断是否会产生稳态误差：给被控对象输入0，判断被控对象会不会自发偏移
• 判断稳态误差的方向：给被控对象输入0，自发偏移方向即为稳态误差方向

积分项I

• 一般配合P使用，也叫做PI控制（电机控速器定速控制）
• 含有比例项和积分项的PID输出值：
  $out(t)=K_p\ast error(t)+K_i\ast {\int }_0^{t}error(t)dt$
• 积分项的输出值取决于0~t所有时刻误差的积分，与历史时刻有关。积分项将历史所有时刻的误差累积，乘上积分项系数$K_i$后作为积分项输出值
• 积分项用于弥补纯比例项产生的稳态误差，若系统持续产生误差，则积分项会不断累积误差，直到控制器产生动作，让稳态误差消失
• $K_i$越大，积分项权重越大，稳态误差消失越快，但系统滞后性也会随之增加

微分项D

• 一般配合PI或单独配合P使用（电机定位控制，平衡摆）

• 含有比例项、积分项和微分项的PID输出值：
  $out(t)=K_p\ast error(t)+K_i\ast {\int }_0^{t}error(t)dt+K_d\ast \frac{derror(t)}{dt}$

• 微分项的输出值取决于当前时刻误差变化的斜率，与当前时刻附近误差变化的趋势有关。当误差急剧变化时，微分项会负反馈输出相反的作用力，阻碍误差急剧变化

• 斜率一定程度上反映了误差未来的变化趋势，这使得微分项具有“预测未来，提前调控”的特性

• 微分项给系统增加阻尼，可以有效防止系统超调，尤其是惯性比较大的系统

• $K_d$越大，微分项权重越大，系统阻尼越大，但系统卡顿现象也会随之增加

形式

离散型PID

$out(k)=K_p\ast error(k)+K_i\ast {\sum }_{j=0}^{k}error(j)+K_d\ast (error(k)-error(k-1))$

无论哪种情景下用哪种PID都可以

位置式PID/全量式PID

• 不止能控制位置，几乎能覆盖所有PID应用场景，速度控制、位置控制，温度控制姿态控制
  $out(k)=K_p\ast error(k)+K_i\ast {\sum }_{j=0}^{k}error(j)+K_d\ast (error(k)-error(k-1))$

增量式PID

$\Delta out(k)=K_p\ast (error(k)-error(k-1))+K_i\ast error(k)+K_d\ast (error(k)-2\ast error(k-1)+error(k-2))$
用$out+=\Delta out$增量式和位置式没有差别

调参

• 一般是按P，I，D顺序调
• 数量级看 输出范围/输入范围