集合的势(基数)
等势
如果两个集合 A , B A,B A,B 之间存在一个映射是一一对应(双射),我们就称两个集合 等势/具有相同的基数 .
形象的说法,有这么一种规则,可以让学生 a ∈ A a\in A a∈A 坐到唯一对应的座位 b ∈ B b\in B b∈B 上,而且教室 Y Y Y 中没有闲置座位 b ∈ B b\in B b∈B . 教室坐满了,每个人一个位置 .
这引入了一个集合之间的一个关系 X R Y : X 与 Y 等势 X\mathcal{R}Y:X与Y等势 XRY:X与Y等势 , 它是个等价关系,因此可以记集合 A , B A,B A,B 等势为 A ∼ B A\sim B A∼B .
等势关系把所有集合划分为由彼此等价的集合组成的类,同一类集合具有相同的数量(等势),而不同类集合具有不同的元素数量。
集合 X X X 所属的类称为集合 X X X 的势或基数类。记为 card X \text{card}X cardX . X ∼ Y ⇔ card X = card Y X\sim Y\Leftrightarrow \text{card} X=\text{card}{Y} X∼Y⇔cardX=cardY .
这种等价类结构的意义在于,如果想要比较两个集合所含元素数量的大小,没必要一个一个去数,也就是借助中间集合自然数集 N = { 1 , 2 , 3 , ⋯ } N=\{1,2,3,\cdots\} N={1,2,3,⋯} 作比较,而可以直接通过建立映射的方法来比较。
比较基数类的大小
如果集合 X X X 与集合 Y Y Y 的某个子集等势,我们就说集合 X X X 的基数类不大于集合 Y Y Y 的基数类,并记 card X ≤ card Y : = ( ∃ Z ⊂ Y ( card X = card Z ) ) \text{card} X\leq \text{card}Y:=(\exists Z\subset Y(\text{card}X=\text{card}Z)) cardX≤cardY:=(∃Z⊂Y(cardX=cardZ))
如果 X ⊂ Y X\subset Y X⊂Y , 那么明显有 card X ≤ card Y \text{card}X\leq \text{card}Y cardX≤cardY . 但这并不妨碍可以存在 card Y ≤ card X \text{card} Y\leq \text{card} X cardY≤cardX , 即便 X X X 是 Y Y Y 的真子集 .比如,映射 x ↦ x 1 − ∣ x ∣ = { x 1 − x = − 1 + 1 1 − x 0 < x < 1 x 1 + x = 1 − 1 1 + x − 1 < x ≤ 0 x\mapsto \frac{x}{1-|x|}=\begin{cases}\frac{x}{1-x}=-1+\frac{1}{1-x}&0<x<1 \\ \frac{x}{1+x}=1-\frac{1}{1+x}& -1< x\le 0\end{cases} x↦1−∣x∣x={1−xx=−1+1−x11+xx=1−1+x10<x<1−1<x≤0 就是 R \mathbb{R} R 的子集 ( − 1 , 1 ) (-1,1) (−1,1) 到 R \mathbb{R} R 的双射 . 这说明 card ( − 1 , 1 ) = card R \text{card}(-1,1)=\text{card}\mathbb{R} card(−1,1)=cardR .
一个集合能够和自身的一个真子集等势,这是无穷集的特征。按照戴德金的说法,一个集合不与自己的任何真子集等价,它就是 有限集 ,反之是 无穷集 。
基数类的有序化
基数类之间的不等关系使得基数类有序。
-
自反性: card X ≤ card X \text{card}X\leq \text{card}X cardX≤cardX
-
传递性: ( card X ≤ card Y ) ∧ ( card Y ≤ card Z ) ⇒ ( card X ≤ card Z ) (\text{card}X\leq \text{card}Y )\wedge(\text{card} Y\leq \text{card}Z)\Rightarrow (\text{card}X\leq \text{card}Z) (cardX≤cardY)∧(cardY≤cardZ)⇒(cardX≤cardZ)
-
反对称性(施罗德-伯恩斯坦定理): ( card X ≤ card Y ) ∧ ( card Y ≤ card X ) ⇒ ( card X = card Y ) (\text{card}X\leq \text{card}Y )\wedge(\text{card} Y\leq \text{card}X)\Rightarrow (\text{card}X= \text{card}Y) (cardX≤cardY)∧(cardY≤cardX)⇒(cardX=cardY)
-
可比性(康托尔定理):$\forall X\forall Y(\text{card} X\le \text{card}Y)\vee(\text{card} Y\le \text{card}X) $
基数类是线性有序的。
( card X < card Y ) : = ( card X ≤ card Y ) ∧ ( card X ≠ card Y ) (\text{card}X <\text{card} Y):=(\text{card}X \le \text{card} Y)\wedge(\text{card}X \neq \text{card} Y) (cardX<cardY):=(cardX≤cardY)∧(cardX=cardY)
本身的势小于幂集的势
设 P ( X ) \mathcal{P}(X) P(X) 表示 X X X 的一切子集组成的集合,即 X X X 的幂集。
card X < card P ( X ) \text{card} X<\text{card}\mathcal{P}(X) cardX<cardP(X)
证明:
若 X = ∅ X=\varnothing X=∅ , P ( X ) = ∅ \mathcal{P}(X)=\varnothing P(X)=∅ , 显然成立
假设 X ≠ ∅ X\neq \varnothing X=∅ . 可以作双射 x ↦ f { x } x\overset{f}\mapsto \{x\} x↦f{x} , 即 f : X → { { x } ∣ x ∈ X } ⊂ P ( X ) f:X\to \{\{x\}|x\in X\}\subset \mathcal{P}(X) f:X→{{x}∣x∈X}⊂P(X) . 因此 $ \text{card}X\leq \text{card}\mathcal{P}(X)$ .
假设存在双射 f : X → P ( X ) f:X\to \mathcal{P}(X) f:X→P(X) , 可取 A = { x ∣ ( x ∈ X ) ∧ ( x ∉ f ( x ) } ⊂ X A=\{x|(x\in X)\wedge(x\notin f(x)\}\subset X A={x∣(x∈X)∧(x∈/f(x)}⊂X .
A ∈ P ( X ) A\in \mathcal{P}(X) A∈P(X) , 因此存在 a ∈ X a\in X a∈X , 使得 f ( a ) = A f(a)=A f(a)=A .
如果 a ∈ A a\in A a∈A , 则 a ∉ f ( a ) = A a\not \in f(a)=A a∈f(a)=A . 产生矛盾 .
如果 a ∉ A a\notin A a∈/A , 则 a ∈ f ( a ) = A a\in f(a)=A a∈f(a)=A . 产生矛盾 .
这违反了排中律 . 因此不存在双射 f : X → P ( X ) f:X\to \mathcal{P}(X) f:X→P(X) ,即 card X ≠ card P ( X ) \text{card}X\neq\text{card} \mathcal{P}(X) cardX=cardP(X)
综上所述, card X < card P ( X ) \text{card} X<\text{card}\mathcal{P}(X) cardX<cardP(X)
这说明,没有最大的基数类,因为一个集合的幂集的基数类更大。
而且,无穷集也是有基数类的大小之分的。
公理化集合论
本节的集合论公理化系统确保了集合概念的合理性。
外延公理 集合 A A A 与集合 B B B 相等,当且仅当它们所具有的各元素是相同的
外延公理表示,一个集合只和它所拥有的元素有关。
在实际应用中,外延公理告诉我们,要判断 A = B A=B A=B , 就要验证 ∀ x ( ( x ∈ A ) ⇔ ( x ∈ B ) ) \forall x((x\in A)\Leftrightarrow(x\in B)) ∀x((x∈A)⇔(x∈B)) .
集合相等,元素相同
分离公理 任何集合 A A A 和性质 P P P 都对应一个集合 B B B , 其元素是且仅是 A A A 中具有性质 P P P 的各元素
简而言之,就是 A A A 是一个集合,则 B = { x ∈ A ∣ P ( x ) } B=\{x\in A|P(x)\} B={x∈A∣P(x)} 也是一个集合 .
分离公理在研究很多数学结构时具有很重要的作用,这时我们可以从一些集合中分离出具有某种性质的元素组成的子集。
比如,由分离定理可知,任何集合 X X X 都具有空子集 ∅ X = { x ∈ X ∣ x ≠ x } \varnothing_X=\{x\in X|x\neq x\} ∅X={x∈X∣x=x} , 而由外延定理可知, ∅ X = ∅ Y \varnothing_X=\varnothing_Y ∅X=∅Y 对于任何两个集合 X X X 和 Y Y Y 都成立 . 这说明空集是唯一的 .
由分离定理还可以知道,如果 A A A 和 B B B 都是集合,则 A − B = { x ∈ A ∣ x ∉ B } A-B=\{x\in A|x\notin B\} A−B={x∈A∣x∈/B} 也是一个集合 . 特别地,如果 M M M 是一个集合, A A A 是它的一个子集,则 C M A C_MA CMA 也是一个集合 .
并集公理 对于以集合为元素的任何集合 M M M ,都存在一个被称为集合 M M M 的并集的集合 ∪ M \cup M ∪M , 其元素是且仅是 M M M 的各元素所包含的那些元素。
集合的集合通常称为集合族 .
由并集公理知,集合的并集还是集合,并且 x ∈ ∪ M ⇔ ∃ X ( ( X ∈ M ) ∧ ( x ∈ X ) ) x\in \cup M\Leftrightarrow \exists X((X\in M)\wedge(x\in X)) x∈∪M⇔∃X((X∈M)∧(x∈X))
有了并集公理和分离公理,我们可以把集合族 M M M 的交集定义为 ∩ M : = { x ∈ ∪ M ∣ ∀ X ( ( X ∈ M ⇒ x ∈ X ) ) } \cap M:=\{x\in \cup M|\forall X((X\in M\Rightarrow x\in X))\} ∩M:={x∈∪M∣∀X((X∈M⇒x∈X))}
配对公理 对于任何集合 X , Y X, Y X,Y , 存在一个集合 Z Z Z , 其元素仅为 X X X 和 Y Y Y
集合 { X , Y } \{X,Y\} {X,Y} 即为 X X X 与 Y Y Y 的无序偶 . 序偶与无序偶的区别在于,序偶能够分出前后,比如可以这么定义 ( X , Y ) : = { { X , X } , { X , Y } } (X,Y):=\{\{X,X\},\{X,Y\}\} (X,Y):={{X,X},{X,Y}} ,即序偶可以通过无序偶来引入 .
子集之集公理 对于任何集合 X X X , 存在一个集合 P ( X ) \mathcal{P}(X) P(X) , 其元素是且仅是 X X X 的所有子集 .
简而言之,对于给定集合,其所有子集组成的集合是存在的,称为幂集 .
根据分离公理和子集之集公理,我们可以通过序偶来定义笛卡尔积: X × Y : = { p ∈ P ( P ( X ) ∪ P ( Y ) ) ∣ p = ( x , y ) ∧ ( x ∈ X ) ∧ ( y ∈ Y ) } X\times Y:=\{p\in \mathcal{P}(\mathcal{P}(X)\cup\mathcal{P}(Y))|p=(x,y)\wedge(x\in X)\wedge(y\in Y)\} X×Y:={p∈P(P(X)∪P(Y))∣p=(x,y)∧(x∈X)∧(y∈Y)}
以上公理限制了形成新集合的 5 种方法 . 根据外延定理,给出所有的元素,可以确定一个集合 . 根据分离定理,在集合中选取元素可以得到新的集合子集 . 根据并集公理,可以通过取元素的并集得到一个新集合 . 根据配对公理,可以从两个集合构造出无序偶集合 . 根据子集之集公理,可以通过集合的所有子集来得到一个幂集。
根据这 5 种方法,并不能构造出所有集合的“集合” . 事实上,根据 ( card X < card P ( X ) ) (\text{card} X<\text{card}\mathcal{P}(X)) (cardX<cardP(X)) 可知, P ( X ) \mathcal{P}(X) P(X) 中存在不属于 X X X 的集合。设 A A A 为所有集合的集合,则存在 B ⊂ P ( A ) B\subset \mathcal{P}(A) B⊂P(A) , 使得 B ∉ A B\notin A B∈/A . 产生矛盾 . 这避免了罗素悖论 .
定义后继集 X + = X ∪ { X } X^+=X\cup \{X\} X+=X∪{X} , 简而言之,就是在集合 X X X 里面再加上一个单元素集合 { X } \{X\} {X} . 比如 { a , b } \{a,b\} {a,b} 的后继集为 { a , b , { a , b } } \{a,b,\{a,b\}\} {a,b,{a,b}}
此外,如果一个集合包含空集和自身任何一个元素的后继集,我们就称该集合为归纳集 .
无穷公理 归纳集存在
有了无穷公理,再加上之前的公理,就可以建立自然数集 N 0 \mathbb{N}_0 N0 的标准模型(冯·诺依曼方案):
把 N 0 \mathbb{N}_0 N0 定义为各归纳集的交集,即最小归纳集:
∅ , ∅ + = ∅ ∪ { ∅ } = { ∅ } , { ∅ } + = { ∅ } ∪ { { ∅ } } = { ∅ , { ∅ } } , ⋯ \varnothing,\varnothing^+=\varnothing\cup\{\varnothing\}=\{\varnothing\},\{\varnothing\}^+=\{\varnothing\}\cup\{\{\varnothing\}\}=\{\varnothing,\{\varnothing\}\},\cdots ∅,∅+=∅∪{∅}={∅},{∅}+={∅}∪{{∅}}={∅,{∅}},⋯
它就是我们用符号 0 , 1 , 2 , ⋯ 0,1,2,\cdots 0,1,2,⋯ 表示并称之为自然数的那些对象的模型 .
替换公理 设 F ( x , y ) \mathcal{F}(x,y) F(x,y) 是以下命题公式:对于集合 X X X 中的任何元素 x 0 x_0 x0 , 存在唯一的对象 y 0 y_0 y0 , 使得 F ( x 0 , y 0 ) \mathcal{F}(x_0,y_0) F(x0,y0) 成立 . 那么,满足以下条件的对象 y y y 组成一个集合 :存在 x ∈ X x\in X x∈X , 使得 F ( x , y ) \mathcal{F}(x,y) F(x,y) 成立 .
建立分析学时用不到这个公理 .
以上公理组成集合论公理系统,即著名的策梅洛-弗伦克尔公理系统
通常还可以补充以下公理,它独立于以上公理,在分析学中很常用 .
选择公理/策梅洛公里 对于任何由互不相交的非空集合组成的集合族,存在集合 C C C , 使得对于该集合族中的任何集合 X X X , 集合 X ∩ C X\cap C X∩C 只由一个元素组成
换言之,可以从集合族的每个集合中分别选出一个代表元素,并由它们组成集合 C C C
习题
【1】施罗德-伯恩斯定理
a ) 请分别利用施罗德-伯恩斯坦定理和所需双射的直接表示这两种方法,证明直线 R \mathbb{R} R 上的闭区间 { x ∈ R ∣ 0 ≤ x ≤ 1 } \{x\in \mathbb{R}|0\le x\le1\} {x∈R∣0≤x≤1} 与开区间 { x ∈ R ∣ 0 < x < 1 } \{x\in \mathbb{R}|0<x<1\} {x∈R∣0<x<1} 等势 .
证明:
【施罗德-伯恩斯坦定理】
双射 f ( x ) = 1 2 x + 1 4 , 0 ≤ x ≤ 1 f(x)=\frac{1}{2}x+\frac{1}{4},0\le x\le 1 f(x)=21x+41,0≤x≤1 将 [ 0 , 1 ] [0,1] [0,1] 映到 ( 0 , 1 ) (0,1) (0,1) 的子集 [ 1 4 , 3 4 ] [\frac{1}{4},\frac{3}{4}] [41,43] 上 . 因此 card [ − 1 , 1 ] ≤ card ( − 1 , 1 ) \text{card} [-1,1] \le \text{card}(-1,1) card[−1,1]≤card(−1,1)
而 ( 0 , 1 ) (0,1) (0,1) 和 [ 0 , 1 ] [0,1] [0,1] 的子集 ( 0 , 1 ) (0,1) (0,1) 等势,故 card ( − 1 , 1 ) ≤ card [ − 1 , 1 ] \text{card} (-1,1) \le \text{card}[-1,1] card(−1,1)≤card[−1,1]
由施罗德-伯恩斯坦定理得, card [ − 1 , 1 ] = card ( − 1 , 1 ) \text{card} [-1,1] = \text{card}(-1,1) card[−1,1]=card(−1,1)
【直接法】
作映射 f ( x ) = { 1 2 x = − 1 1 3 x = 1 1 n + 2 x = 1 n , n = 2 , 3 , … x 其他情况 f(x)=\begin{cases}\frac{1}{2}&x=-1 \\ \frac{1}{3} & x=1\\ \frac{1}{n+2}& x=\frac{1}{n},n=2,3,\dots \\ x&\text{其他情况}\end{cases} f(x)=⎩ ⎨ ⎧2131n+21xx=−1x=1x=n1,n=2,3,…其他情况 ,则 f f f 将 [ − 1 , 1 ] [-1,1] [−1,1] 映到 ( − 1 , 1 ) (-1,1) (−1,1) , 且是双射,其逆映射为 f − 1 ( y ) = { − 1 y = 1 2 1 y = 1 3 1 n − 2 y = 1 n , n = 4 , 5 , … y 其他情况 f^{-1}(y)=\begin{cases}-1&y=\frac{1}{2} \\ 1 & y=\frac{1}{3}\\ \frac{1}{n-2}& y=\frac{1}{n},n=4,5,\dots \\ y&\text{其他情况}\end{cases} f−1(y)=⎩ ⎨ ⎧−11n−21yy=21y=31y=n1,n=4,5,…其他情况
因此直线 R \mathbb{R} R 上的闭区间 { x ∈ R ∣ 0 ≤ x ≤ 1 } \{x\in \mathbb{R}|0\le x\le1\} {x∈R∣0≤x≤1} 与开区间 { x ∈ R ∣ 0 < x < 1 } \{x\in \mathbb{R}|0<x<1\} {x∈R∣0<x<1} 等势 .
b) 分析书上给出的施罗德-伯恩斯坦定理的一个证明。
解:
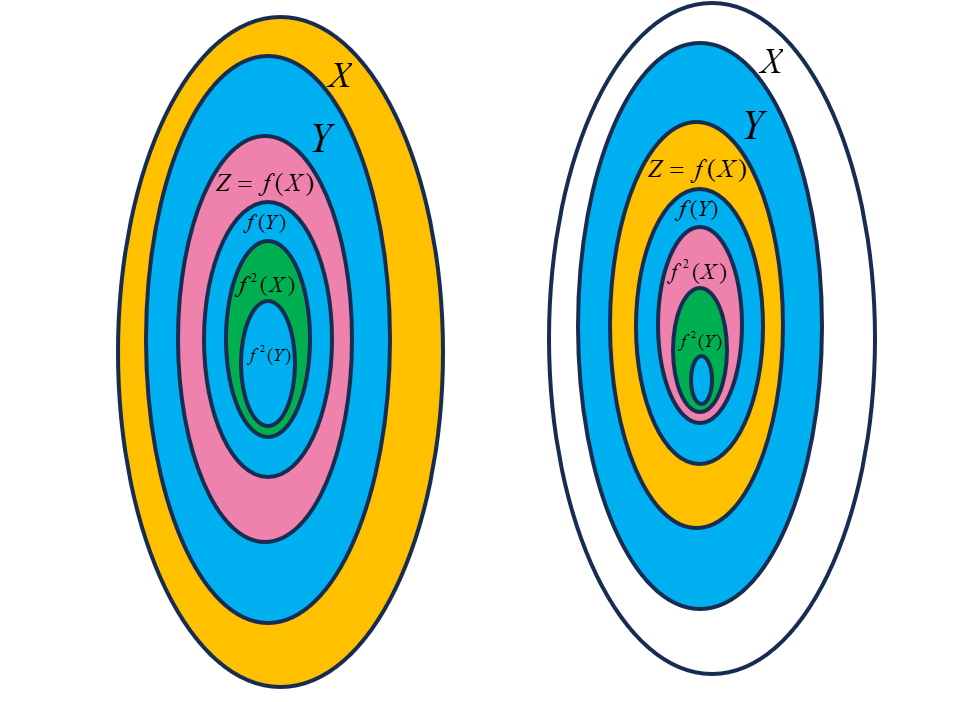
如果 card Y ≤ card X \text{card} Y\le \text{card} X cardY≤cardX 且 card X ≤ card Y \text{card} X\le \text{card} Y cardX≤cardY , 那么 Y Y Y 对等于 X X X 的一个子集 X ′ X' X′ , X X X 对等于 Y Y Y 的一个子集 Y ′ Y' Y′ . 于是可以拓充 Y Y Y 得到 Y ′ ′ Y'' Y′′ , 使得 Y ⊂ Y ′ ′ Y\subset Y'' Y⊂Y′′ 且 Y ′ ′ Y'' Y′′ 对等于 X X X . 于是问题转换为 ( Y ′ ⊂ Y ⊂ Y ′ ′ ) ∧ ( card Y ′ = card Y ′ ′ ) ⇒ ( card Y = card Y ′ ) (Y'\subset Y\subset Y'')\wedge(\text{card} Y'= \text{card} Y'')\Rightarrow (\text{card} Y= \text{card} Y') (Y′⊂Y⊂Y′′)∧(cardY′=cardY′′)⇒(cardY=cardY′)
为了便于理解,修改记号,所证问题变为 ( Z ⊂ Y ⊂ X ) ∧ ( card X = card Z ) ⇒ ( card X = card Y ) (Z\subset Y\subset X)\wedge(\text{card} X= \text{card} Z)\Rightarrow (\text{card} X= \text{card} Y) (Z⊂Y⊂X)∧(cardX=cardZ)⇒(cardX=cardY)
设 f : X → Z f:X\to Z f:X→Z 是双射,我们可以构造下面的映射 g : X → Y g:X\to Y g:X→Y
g ( x ) = { f ( x ) x ∈ ∪ n = 1 ∞ ( f n ( X ) − f n ( Y ) ) x x ∉ ∪ n = 1 ∞ ( f n ( X ) − f n ( Y ) ) g(x)=\begin{cases}f(x)& x\in\cup_{n=1}^{\infty}(f^n(X)-f^n(Y)) \\ x&x\notin\cup_{n=1}^{\infty}(f^n(X)-f^n(Y))\end{cases} g(x)={f(x)xx∈∪n=1∞(fn(X)−fn(Y))x∈/∪n=1∞(fn(X)−fn(Y))
记 A = ∪ n = 0 ∞ ( f n ( X ) − f n ( Y ) ) A=\cup_{n=0}^{\infty}(f^n(X)-f^n(Y)) A=∪n=0∞(fn(X)−fn(Y)) .
设 y ∈ Y y\in Y y∈Y , 则要么 y ∉ A y\notin A y∈/A , 这时可令 y y y 对应本身 , 即有 g ( y ) = y g(y)=y g(y)=y .
要么 y ∈ A ⊂ Z y\in A \sub Z y∈A⊂Z , 令 y y y 对应于 f − 1 ( y ) f^{-1}(y) f−1(y) , 即 g ( f − 1 ( y ) ) = y g(f^{-1}(y))=y g(f−1(y))=y.
故 g g g 是满射 .
设 g ( x 1 ) = g ( x 2 ) g(x_1)=g(x_2) g(x1)=g(x2) . 这时有四种情况
x 1 , x 2 ∉ A x_1,x_2\notin A x1,x2∈/A . 这说明 x 1 = x 2 x_1=x_2 x1=x2
x 1 ∈ A , x 2 ∉ A x_1\in A,x_2\notin A x1∈A,x2∈/A . g ( x 1 ) = g ( x 2 ) ⇒ f ( x 1 ) = x 2 g(x_1)=g(x_2)\Rightarrow f(x_1)=x_2 g(x1)=g(x2)⇒f(x1)=x2 . 由 x 1 ∈ A x_1\in A x1∈A 很容易推出 f ( x 1 ) ∈ A f(x_1)\in A f(x1)∈A . 这说明 x 2 ∈ A x_2\in A x2∈A . 产生矛盾. 因此这种情形不可能出现 .
x 1 ∉ A , x 2 ∈ A x_1\notin A,x_2\in A x1∈/A,x2∈A , 同理,不可能出现 .
x 1 ∈ A , x 2 ∈ A ⇒ f ( x 1 ) = f ( x 2 ) ⇒ x 1 = x 2 x_1\in A,x_2\in A\Rightarrow f(x_1)=f(x_2)\Rightarrow x_1=x_2 x1∈A,x2∈A⇒f(x1)=f(x2)⇒x1=x2
故 g g g 是单射 .






















 559
559

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








