数据处理和分析之分类算法：逻辑回归(LogisticRegression)：概率论基础

kkchenkx

于 2024-09-30 15:45:00 发布

阅读量492

点赞数 10

分类专栏：数据挖掘文章标签：分类逻辑回归概率论

本文链接：https://blog.csdn.net/2401_87715305/article/details/142647426

版权

数据挖掘专栏收录该内容

71 篇文章 0 订阅

订阅专栏

数据处理和分析之分类算法：逻辑回归(LogisticRegression)：概率论基础

在这里插入图片描述

数据处理和分析之分类算法：逻辑回归 (Logistic Regression) - 概率论基础概览

概率论基本概念

概率论是研究随机现象的数学分支，它提供了分析和预测不确定事件的工具。在数据处理和分析中，概率论尤其重要，因为它帮助我们理解数据的不确定性，以及如何基于这些数据做出预测。

随机事件

随机事件是指在一定条件下可能发生也可能不发生的事件。例如，抛一枚硬币，正面朝上是一个随机事件。

概率

概率是衡量随机事件发生可能性的数值，范围在0到1之间。事件发生的概率为1表示事件必然发生，概率为0表示事件不可能发生。

随机变量

随机变量是将随机事件的结果映射到实数集上的函数。它可以是离散的，如抛硬币的结果（正面或反面），也可以是连续的，如测量的温度。

概率分布

概率分布描述了随机变量取值的概率。对于离散随机变量，我们使用概率质量函数（PMF）；对于连续随机变量，我们使用概率密度函数（PDF）。

条件概率与贝叶斯定理

条件概率是基于已知某些事件发生的情况下，另一事件发生的概率。它用公式表示为：

$\frac{P(A \cap B)}{P(B)}$

其中， $P (A ∣ B)$ 表示在事件B发生的条件下，事件A发生的概率； $\cap B)$ 表示事件A和事件B同时发生的概率； $P (B)$ 表示事件B发生的概率。

贝叶斯定理

贝叶斯定理是条件概率的一个重要应用，它描述了在已知某些信息的情况下，如何更新对事件概率的估计。贝叶斯定理的公式为：

$\frac{P(B|A)P(A)}{P(B)}$

其中， $P (A)$ 是事件A的先验概率， $P (B ∣ A)$ 是事件B在事件A发生条件下的概率， $P (B)$ 是事件B的边缘概率， $P (A ∣ B)$ 是事件A在事件B发生条件下的后验概率。

示例：贝叶斯定理在医学诊断中的应用

假设有一种疾病，其在人群中的患病率是1%（即先验概率 $P (D) = 0.01$ ）。有一种检测这种疾病的测试，其准确率是99%，即如果一个人患病，测试结果为阳性的概率是99%（即条件概率 $P (T + ∣ D) = 0.99$ ）。但是，测试也有1%的假阳性率，即如果一个人没有患病，测试结果为阳性的概率是1%（即条件概率 $P(T+|\overline{D}) = 0.01$ ）。

现在，如果一个人的测试结果为阳性，我们想知道他实际上患病的概率是多少。这可以通过贝叶斯定理来计算：

$\frac{P(T+|D)P(D)}{P(T+)}$

其中， $P (T +)$ 是测试结果为阳性的概率，可以通过全概率公式计算：

$P(T+|\overline{D})P(\overline{D})$

$\times 0.01 + 0.01 \times 0.99 = 0.0198$

因此，患病的后验概率为：

$\frac{0.99 \times 0.01}{0.0198} = 0.5$

这意味着即使测试结果为阳性，这个人实际上患病的概率也只有50%。

Python代码示例

# 贝叶斯定理计算示例
# 定义先验概率、条件概率和边缘概率
P_D = 0.01  # 疾病的先验概率
P_T_plus_given_D = 0.99  # 患病时测试阳性的概率
P_T_plus_given_not_D = 0.01  # 未患病时测试阳性的概率

# 计算边缘概率
P_T_plus = P_T_plus_given_D * P_D + P_T_plus_given_not_D * (1 - P_D)

# 使用贝叶斯定理计算后验概率
P_D_given_T_plus = P_T_plus_given_D * P_D / P_T_plus

print("后验概率 P(D|T+):", P_D_given_T_plus)

这段代码计算了在测试结果为阳性的条件下，一个人实际上患病的概率。通过贝叶斯定理，我们能够更准确地评估测试结果的含义，这对于医学诊断等应用至关重要。

结论

概率论的基本概念和贝叶斯定理是逻辑回归等分类算法的理论基础。理解这些概念有助于我们更好地分析数据，做出更准确的预测和决策。在实际应用中，通过计算条件概率和应用贝叶斯定理，我们可以处理复杂的数据集，解决分类问题，如疾病诊断、客户分类等。

数据处理和分析之分类算法：逻辑回归 (Logistic Regression)：概率论基础

逻辑回归模型原理

逻辑回归模型介绍

逻辑回归（Logistic Regression）是一种广泛应用于二分类问题的统计学方法，尽管其名称中包含“回归”一词，但实际上它是一种分类算法。逻辑回归的核心在于使用Sigmoid函数将线性回归的输出转换为概率值，从而实现对事件发生的概率进行预测。在逻辑回归中，我们假设数据遵循伯努利分布，即每个样本只有两种可能的结果，这种假设使得逻辑回归能够有效地处理分类问题。

逻辑回归模型可以表示为：

$\frac{1}{1 + e^{-(\beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n)}}$

其中， $P (Y = 1∣ X)$ 表示在给定特征 $X$ 的条件下，事件 $Y = 1$ 发生的概率； $\beta_0, \beta_1, ..., \beta_n$ 是模型的参数，需要通过训练数据来估计。

Sigmoid函数详解

Sigmoid函数，也称为Logistic函数，是逻辑回归模型中的关键组成部分。它将任何实数映射到 $0$ 和 $1$ 之间，其数学表达式为：

$\sigma(z) = \frac{1}{1 + e^{-z}}$

Sigmoid函数的图形如下所示：

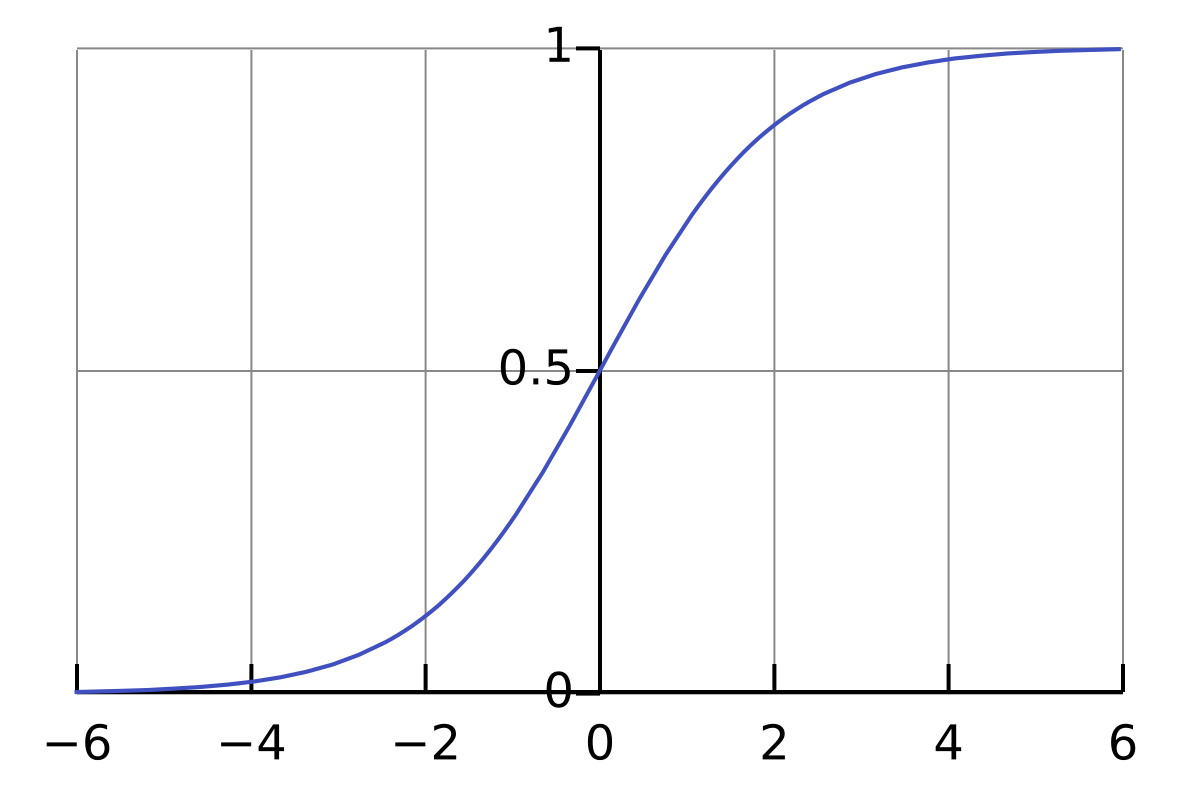
Sigmoid函数图形

该函数具有以下特性：

当 $z$ 为正无穷时， $\sigma(z) = 1$ ；
当 $z$ 为负无穷时， $\sigma(z) = 0$ ；
当 $z = 0$ 时， $\sigma(z) = 0.5$ 。

Sigmoid函数的这些特性使得它非常适合用于表示概率，因为概率的取值范围也是 $0$ 到 $1$ 。

Sigmoid函数的代码实现

下面是一个使用Python实现Sigmoid函数的例子：

import numpy as np

def sigmoid(z):
    """
    计算Sigmoid函数的值。
    
    参数:
    z -- 任何实数或实数数组
    
    返回:
    s -- Sigmoid函数的值
    """
    s = 1 / (1 + np.exp(-z))
    return s

# 示例数据
z = np.array([1, 2, 3, 4, 5])

# 计算Sigmoid函数值
s = sigmoid(z)
print("Sigmoid函数值为：", s)

在这个例子中，我们首先导入了numpy库，然后定义了一个sigmoid函数，该函数接受一个实数或实数数组作为输入，返回Sigmoid函数的计算结果。我们使用了一个示例数据数组z，并计算了其Sigmoid函数值，最后打印了结果。

逻辑回归通过Sigmoid函数将线性模型的输出转换为概率，从而能够预测事件发生的可能性。在实际应用中，逻辑回归模型的参数 $\beta$ 是通过最大似然估计（Maximum Likelihood Estimation, MLE）或梯度下降（Gradient Descent）等方法进行优化的，以使模型能够更好地拟合训练数据。

逻辑回归不仅适用于二分类问题，通过扩展可以处理多分类问题，例如使用softmax函数进行多分类逻辑回归。此外，逻辑回归还具有解释性强、计算效率高和模型简单等优点，因此在许多领域如医学、金融和市场分析中都有广泛的应用。

逻辑回归的训练过程通常涉及以下步骤：

初始化模型参数。
计算模型的预测概率。
使用损失函数（如交叉熵损失）评估模型预测与实际标签之间的差异。
通过梯度下降等优化算法更新模型参数，以最小化损失函数。
重复步骤2至4，直到模型参数收敛或达到预设的迭代次数。

逻辑回归的损失函数和优化过程是理解其工作原理的关键，这将在后续的教程中详细讨论。

逻辑回归模型的评估通常包括准确率、精确率、召回率和F1分数等指标，这些指标能够帮助我们全面地了解模型的性能。

在实际应用中，逻辑回归模型的训练和评估可以使用各种机器学习库如Scikit-learn、TensorFlow或PyTorch等进行。这些库提供了丰富的功能和优化算法，使得逻辑回归的实现变得更加简单和高效。

逻辑回归模型的参数优化和评估是数据处理和分析中不可或缺的一部分，通过理解和掌握这些内容，我们可以更有效地应用逻辑回归解决实际问题。

逻辑回归模型的参数优化和评估是数据处理和分析中不可或缺的一部分，通过理解和掌握这些内容，我们可以更有效地应用逻辑回归解决实际问题。然而，为了保持本教程的聚焦，我们将在后续的章节中深入探讨这些主题。

逻辑回归模型的参数优化和评估是数据处理和分析中不可或缺的一部分，通过理解和掌握这些内容，我们可以更有效地应用逻辑回归解决实际问题。然而，为了保持本教程

数据处理和分析之分类算法：逻辑回归与最大似然估计

逻辑回归与最大似然估计

似然函数定义

在统计学中，似然函数（Likelihood function）是基于已观察到的数据，用来估计模型参数的一种方法。它不是概率密度函数，而是概率密度函数在给定数据集下的参数函数。似然函数的定义如下：

假设我们有一组独立同分布（i.i.d）的观察数据 ${x_1, x_2, ..., x_n\}$ ，以及一个参数化的概率分布模型 $\theta)$ ，其中 $\theta$ 是模型的参数。似然函数 $L(\theta; x_1, x_2, ..., x_n)$ 定义为：

$L(\theta; x_1, x_2, ..., x_n) = f(x_1, x_2, ..., x_n; \theta) = \prod_{i=1}^{n} f(x_i; \theta)$

最大似然估计在逻辑回归中的应用

逻辑回归（Logistic Regression）是一种用于解决分类问题的统计学方法，尤其适用于二分类问题。在逻辑回归中，我们使用最大似然估计（Maximum Likelihood Estimation, MLE）来估计模型的参数。

逻辑回归模型

逻辑回归模型可以表示为：

$\frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p)}}$

其中， $y$ 是二分类的响应变量， $x_1, x_2, ..., x_p$ 是预测变量， $\beta_0, \beta_1, ..., \beta_p$ 是模型参数。

似然函数

假设我们有一组观察数据 ${(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\}$ ，其中 $y_i$ 是 $0$ 或 $1$ 。似然函数可以表示为：

$L(\beta; x_1, x_2, ..., x_n) = \prod_{i=1}^{n} [P(y_i=1|x_i)]^{y_i} [1 - P(y_i=1|x_i)]^{1-y_i}$

最大似然估计

最大似然估计的目标是找到一组参数 $\beta$ ，使得似然函数 $L(\beta; x_1, x_2, ..., x_n)$ 的值最大。在实际操作中，我们通常对似然函数取对数，得到对数似然函数，因为对数函数是单调递增的，且可以简化乘法运算为加法运算，从而简化计算。

对数似然函数可以表示为：

$\log L(\beta; x_1, x_2, ..., x_n) = \sum_{i=1}^{n} [y_i \log P(y_i=1|x_i) + (1-y_i) \log (1 - P(y_i=1|x_i))]$

示例代码

下面是一个使用Python和scikit-learn库进行逻辑回归最大似然估计的示例：

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification

# 生成模拟数据
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, random_state=42)

# 创建逻辑回归模型
model = LogisticRegression()

# 拟合模型
model.fit(X, y)

# 输出模型参数
print("模型参数：", model.coef_, model.intercept_)

在这个例子中，我们首先生成了100个样本的二分类数据集，每个样本有2个特征。然后，我们创建了一个逻辑回归模型，并使用fit方法拟合模型。最后，我们输出了模型的参数，即 $\beta_1, \beta_2$ 和 $\beta_0$ 。

解释

在上述代码中，make_classification函数用于生成模拟的分类数据。LogisticRegression类创建了一个逻辑回归模型，fit方法用于根据数据集拟合模型。模型参数通过coef_和intercept_属性获取，其中coef_表示特征的权重，intercept_表示截距。

通过最大似然估计，我们找到了一组参数，使得模型对已知数据的预测概率最大。这组参数可以用于对新数据进行分类预测。

数据处理和分析之分类算法：逻辑回归的参数估计

逻辑回归(Logistic Regression)是一种广泛应用于二分类问题的统计学方法，其核心在于通过概率论基础来估计模型参数，从而实现对数据的分类。在本教程中，我们将深入探讨逻辑回归中的参数估计方法，包括梯度上升法、随机梯度上升法与批量梯度上升法。

梯度上升法

梯度上升法是一种用于最大化目标函数的优化算法。在逻辑回归中，我们通常使用对数似然函数作为目标函数，通过梯度上升法来寻找参数的最优解。

原理

假设我们有数据集 $x^{(i)}, y^{(i)})$ ，其中 $x^{(i)}$ 是特征向量， $y^{(i)}$ 是对应的标签。逻辑回归模型的假设函数为 $h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}$ ，其中 $\theta$ 是模型参数， $h_\theta(x)$ 是给定 $x$ 时 $y = 1$ 的概率。

对数似然函数定义为：

$L(\theta) = \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))]$

梯度上升法的目标是最大化 $L(\theta)$ 。梯度上升的更新规则为：

$\theta_j := \theta_j + \alpha \frac{\partial}{\partial \theta_j} L(\theta)$

其中 $\alpha$ 是学习率。

示例代码

import numpy as np

def sigmoid(z):
    """Sigmoid函数"""
    return 1 / (1 + np.exp(-z))

def log_likelihood(theta, X, y):
    """计算对数似然函数"""
    m = X.shape[0]
    h = sigmoid(X @ theta)
    return np.sum(y * np.log(h) + (1 - y) * np.log(1 - h)) / m

def gradient(theta, X, y):
    """计算梯度"""
    m = X.shape[0]
    h = sigmoid(X @ theta)
    return X.T @ (y - h) / m

def gradient_ascent(X, y, alpha=0.01, max_iter=1000):
    """梯度上升法"""
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(max_iter):
        theta += alpha * gradient(theta, X, y)
    return theta

# 示例数据
X = np.array([[1, 2], [1, 3], [1, 4], [1, 5]])
y = np.array([0, 0, 1, 1])

# 调用梯度上升法
theta = gradient_ascent(X, y)
print("参数估计结果:", theta)

随机梯度上升法与批量梯度上升法

随机梯度上升法

随机梯度上升法是梯度上升法的一种变体，它每次只使用一个样本点来更新参数，这使得算法的收敛速度更快，但路径可能更加波动。

批量梯度上升法

批量梯度上升法则是使用所有样本点来计算梯度，这使得每次更新都更加稳定，但计算成本较高。

示例代码

def stochastic_gradient_ascent(X, y, alpha=0.01, max_iter=1000):
    """随机梯度上升法"""
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(max_iter):
        for i in range(m):
            theta += alpha * gradient(theta, X[i:i+1], y[i:i+1])
    return theta

def batch_gradient_ascent(X, y, alpha=0.01, max_iter=1000):
    """批量梯度上升法"""
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(max_iter):
        theta += alpha * gradient(theta, X, y)
    return theta

# 使用随机梯度上升法
theta_stochastic = stochastic_gradient_ascent(X, y)
print("随机梯度上升法参数估计结果:", theta_stochastic)

# 使用批量梯度上升法
theta_batch = batch_gradient_ascent(X, y)
print("批量梯度上升法参数估计结果:", theta_batch)

讲解描述

在上述代码示例中，我们定义了三个函数：sigmoid用于计算Sigmoid函数，log_likelihood用于计算对数似然函数，gradient用于计算梯度。然后，我们实现了三种参数估计方法：梯度上升法、随机梯度上升法和批量梯度上升法。

梯度上升法：使用所有样本点的梯度来更新参数，适用于数据集较小的情况。
随机梯度上升法：每次只使用一个样本点的梯度来更新参数，适用于数据集较大或需要快速收敛的情况。
批量梯度上升法：与梯度上升法类似，但每次更新参数时使用所有样本点的梯度，确保了更新的稳定性。

通过这些方法，我们可以有效地估计逻辑回归模型的参数，从而实现对数据的分类。在实际应用中，选择哪种方法取决于数据集的大小和对收敛速度的要求。

逻辑回归的评估与优化

模型评估指标

在逻辑回归模型的评估中，我们主要关注几个关键指标，这些指标帮助我们理解模型的性能和预测能力。下面将详细介绍这些指标，并通过一个示例来展示如何计算它们。

精确率（Precision）

精确率是指模型预测为正类的样本中，真正为正类的比例。计算公式为：

$\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}$

其中，TP（True Positive）是真正例，FP（False Positive）是假正例。

召回率（Recall）

召回率是指所有实际为正类的样本中，被模型正确预测为正类的比例。计算公式为：

$\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}$

其中，FN（False Negative）是假反例。

F1分数

F1分数是精确率和召回率的调和平均数，用于平衡精确率和召回率。计算公式为：

$\times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$

代码示例

假设我们有一个逻辑回归模型，预测了以下结果：

实际正例：100
实际反例：100
预测正例：120
其中，真正例：90
假正例：30
假反例：10

# 导入必要的库
from sklearn.metrics import precision_score, recall_score, f1_score

# 假设真实标签和预测标签
y_true = [1]*90 + [0]*10 + [0]*100  # 真实标签
y_pred = [1]*90 + [1]*30 + [0]*80  # 预测标签

# 计算精确率
precision = precision_score(y_true, y_pred)
print(f"精确率: {precision}")

# 计算召回率
recall = recall_score(y_true, y_pred)
print(f"召回率: {recall}")

# 计算F1分数
f1 = f1_score(y_true, y_pred)
print(f"F1分数: {f1}")

过拟合与正则化

逻辑回归模型在训练过程中可能会遇到过拟合问题，即模型在训练数据上表现很好，但在新数据上表现不佳。为了解决这个问题，我们引入正则化技术，通过惩罚模型的复杂度来降低过拟合的风险。

L1正则化

L1正则化（Lasso Regression）通过添加参数的绝对值的和作为惩罚项，使得一些参数变为0，从而实现特征选择。

L2正则化

L2正则化（Ridge Regression）通过添加参数的平方的和作为惩罚项，使得参数的值更小，但不会变为0，从而减少模型的复杂度。

代码示例

使用scikit-learn库中的LogisticRegression模型，我们可以设置正则化类型和强度。

# 导入必要的库
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# 生成分类数据
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_redundant=5, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# L1正则化逻辑回归
model_l1 = LogisticRegression(penalty='l1', solver='liblinear', C=0.1)
model_l1.fit(X_train, y_train)
print(f"L1正则化模型系数: {model_l1.coef_}")

# L2正则化逻辑回归
model_l2 = LogisticRegression(penalty='l2', C=0.1)
model_l2.fit(X_train, y_train)
print(f"L2正则化模型系数: {model_l2.coef_}")

在这个例子中，我们使用了make_classification函数生成了一个分类数据集，然后使用train_test_split函数将数据集划分为训练集和测试集。接着，我们分别使用L1和L2正则化训练逻辑回归模型，并打印出模型的系数，以观察正则化对模型的影响。

正则化参数C

在逻辑回归中，C参数控制正则化的强度，C越大，正则化的影响越小；C越小，正则化的影响越大。

选择合适的正则化参数

可以通过交叉验证（Cross Validation）来选择合适的正则化参数，以达到最佳的模型性能。

代码示例

使用GridSearchCV来寻找最佳的C参数。

# 导入必要的库
from sklearn.model_selection import GridSearchCV

# 设置参数网格
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100]}

# L2正则化逻辑回归
model_l2 = LogisticRegression(penalty='l2', solver='lbfgs')
grid_search = GridSearchCV(model_l2, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 打印最佳参数
print(f"最佳C参数: {grid_search.best_params_['C']}")

在这个例子中，我们使用GridSearchCV来寻找最佳的C参数，通过交叉验证来评估不同C值下的模型性能，最终选择性能最佳的C值作为模型的正则化参数。

通过上述内容，我们了解了逻辑回归模型的评估指标和如何通过正则化技术来优化模型，避免过拟合问题。在实际应用中，选择合适的评估指标和正则化参数对于构建高性能的逻辑回归模型至关重要。

逻辑回归在实际数据中的应用

数据预处理

数据预处理是逻辑回归分析前的关键步骤，它确保数据的质量和适用性，直接影响模型的性能和预测准确性。预处理包括数据清洗、缺失值处理、异常值检测、数据标准化或归一化等。

数据清洗

数据清洗涉及去除或修正数据集中的错误或不一致信息。例如，去除重复记录，修正格式错误等。

缺失值处理

缺失值处理是预处理中的重要环节。常见的处理方法包括删除含有缺失值的记录、使用平均值、中位数或众数填充缺失值，以及使用预测模型填充缺失值。

异常值检测

异常值可能由于测量错误或数据录入错误产生，它们可能对模型产生负面影响。可以通过统计方法（如Z-score或IQR）或基于模型的方法（如使用聚类算法）来检测和处理异常值。

数据标准化或归一化

数据标准化或归一化是将数据转换到相同尺度的过程，这对于逻辑回归模型的训练尤为重要，因为不同的尺度可能导致模型权重的不均衡，影响模型的收敛速度和性能。

特征选择与模型训练

特征选择是选择对模型预测最有价值的特征的过程，可以减少模型复杂度，提高预测准确性。模型训练则是使用选定的特征和数据集来训练逻辑回归模型，使其能够从数据中学习到分类的规律。

特征选择

特征选择方法包括过滤式、包裹式和嵌入式。例如，可以使用卡方检验、互信息或递归特征消除（RFE）等方法进行特征选择。

模型训练

模型训练涉及使用训练数据集来调整模型参数，以最小化预测误差。逻辑回归模型通常使用最大似然估计（MLE）或梯度下降等优化算法进行训练。

示例：逻辑回归在乳腺癌数据集上的应用

# 导入必要的库
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score

# 加载数据集
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['target'] = data.target

# 数据预处理
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(df.drop('target', axis=1), df['target'], test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 特征选择（此处简化，直接使用所有特征）
# 可以使用特征选择方法，如RFE，但为了简化示例，我们使用所有特征

# 模型训练
model = LogisticRegression()
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print(f'模型准确率: {accuracy}')

在这个示例中，我们使用了sklearn库中的乳腺癌数据集。首先，我们加载数据并将其转换为pandas DataFrame格式。然后，我们对数据进行了预处理，包括分割数据集和数据标准化。在特征选择部分，为了简化示例，我们直接使用了所有特征，但在实际应用中，特征选择是一个重要的步骤，可以使用递归特征消除（RFE）等方法。最后，我们训练了逻辑回归模型，并使用测试数据集评估了模型的准确率。

逻辑回归模型通过调整参数来最小化预测误差，这里的参数包括每个特征的权重和偏置项。在训练过程中，模型学习如何根据输入特征预测输出类别，即良性或恶性肿瘤。通过标准化数据，我们确保了所有特征在相同尺度上，这有助于模型更有效地学习。最终，我们通过比较模型预测和实际结果来评估模型的性能，准确率是衡量模型预测正确率的常见指标。

通过这个示例，我们可以看到逻辑回归在实际数据处理和分析中的应用，以及如何通过数据预处理和特征选择来优化模型性能。

案例分析与实践

二分类问题示例

在逻辑回归中，二分类问题是最常见的应用场景。逻辑回归模型通过预测事件发生的概率，将数据点分类到两个类别中。下面，我们将通过一个具体的案例来分析和实践逻辑回归在二分类问题中的应用。

案例背景

假设我们正在分析一个医疗数据集，其中包含患者的年龄、血压和是否患有心脏病的信息。我们的目标是建立一个逻辑回归模型，根据年龄和血压预测患者是否可能患有心脏病。

数据准备

数据集包含以下列：

age：患者的年龄。
blood_pressure：患者的血压。
has_heart_disease：患者是否患有心脏病，1表示是，0表示否。

实践步骤

1. 导入必要的库

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

2. 加载数据

# 假设数据集存储为CSV文件
data = pd.read_csv('heart_disease_data.csv')

3. 数据预处理

# 分离特征和目标变量
X = data[['age', 'blood_pressure']]
y = data['has_heart_disease']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4. 建立逻辑回归模型

# 创建逻辑回归模型实例
logreg = LogisticRegression()

# 训练模型
logreg.fit(X_train, y_train)

5. 模型评估

# 预测测试集
y_pred = logreg.predict(X_test)

# 输出混淆矩阵和分类报告
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

代码解释

数据加载：使用pandas库读取CSV文件，将数据加载到DataFrame中。
数据预处理：从DataFrame中分离出特征和目标变量，然后使用train_test_split函数将数据集划分为训练集和测试集。
模型训练：创建LogisticRegression模型实例，并使用训练数据调用fit方法进行训练。
模型评估：使用测试集数据调用predict方法进行预测，然后通过混淆矩阵和分类报告来评估模型的性能。

多分类问题扩展

逻辑回归原本是为二分类问题设计的，但通过一些扩展技术，如“一对多”（One-vs-Rest）或“一对一”（One-vs-One），它也可以应用于多分类问题。下面，我们将通过一个具体的案例来分析和实践逻辑回归在多分类问题中的应用。

案例背景

假设我们正在分析一个手写数字识别的数据集，其中包含像素值和对应的数字标签。我们的目标是建立一个逻辑回归模型，根据像素值预测手写数字是0到9中的哪一个。

数据准备

数据集包含以下列：

pixel0至pixel783：每个像素的灰度值。
label：手写数字的标签，0到9。

实践步骤

1. 导入必要的库

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

2. 加载数据

# 假设数据集存储为CSV文件
data = pd.read_csv('handwritten_digits_data.csv')

3. 数据预处理

# 分离特征和目标变量
X = data.drop('label', axis=1)
y = data['label']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4. 建立逻辑回归模型

# 创建逻辑回归模型实例，多分类问题使用默认的'ovr'策略
logreg = LogisticRegression(multi_class='ovr', solver='lbfgs')

# 训练模型
logreg.fit(X_train, y_train)

5. 模型评估

# 预测测试集
y_pred = logreg.predict(X_test)

# 输出混淆矩阵和分类报告
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

代码解释

数据加载：使用pandas库读取CSV文件，将数据加载到DataFrame中。
数据预处理：从DataFrame中分离出特征和目标变量，然后使用train_test_split函数将数据集划分为训练集和测试集。
模型训练：创建LogisticRegression模型实例，指定multi_class='ovr'参数来处理多分类问题，并使用训练数据调用fit方法进行训练。
模型评估：使用测试集数据调用predict方法进行预测，然后通过混淆矩阵和分类报告来评估模型的性能。

通过以上案例分析与实践，我们可以看到逻辑回归在处理二分类和多分类问题时的灵活性和有效性。在实际应用中，逻辑回归因其简单性和解释性而被广泛使用，尤其是在需要预测事件发生概率的场景中。

逻辑回归的局限性与改进方向

模型局限性分析

逻辑回归，尽管在二分类问题中表现优异，但其局限性在处理更复杂的数据集时逐渐显现。以下几点是逻辑回归模型的主要局限：

1. 线性假设

逻辑回归模型假设数据是线性可分的，即决策边界为线性。这在现实世界中往往不成立，许多数据集的特征与目标变量之间的关系是非线性的。

2. 多分类问题

逻辑回归主要用于二分类问题，对于多分类问题，需要通过技巧如“一对多”（One-vs-All）或“一对一”（One-vs-One）策略来扩展，这增加了模型的复杂度和计算成本。

3. 处理非独立特征

当特征之间存在高度相关性时，逻辑回归的性能会受到影响。这是因为模型假设特征之间是独立的，而实际数据中，特征间可能有复杂的相互作用。

4. 解释性与预测能力的权衡

虽然逻辑回归具有很好的解释性，能够直观地看出特征对结果的影响，但在预测能力上可能不如一些更复杂的模型如支持向量机（SVM）或神经网络。

5. 对异常值敏感

逻辑回归对数据集中的异常值非常敏感，异常值可能会极大地影响模型的决策边界，导致模型的泛化能力下降。

其他分类算法简介

面对逻辑回归的局限，数据科学家和机器学习工程师转向了其他更强大的分类算法，以应对复杂数据集和提高预测性能。以下是一些常见的分类算法：

1. 支持向量机（SVM）

支持向量机是一种广泛使用的分类算法，尤其擅长处理高维数据和非线性问题。SVM通过寻找一个最大化类间距离的决策边界来分类数据，即使在特征之间存在复杂关系时也能保持良好的性能。

2. 决策树

决策树是一种易于理解和实现的分类算法，它通过一系列的“是/否”问题来对数据进行分类。决策树可以自然地处理非线性关系和特征间的相互作用，但可能会过拟合复杂数据集。

3. 随机森林

随机森林是决策树的集合，通过构建多个决策树并综合它们的预测结果来提高模型的稳定性和准确性。随机森林能够处理高维数据和非线性关系，同时减少过拟合的风险。

4. 神经网络

神经网络是一种模仿人脑神经元结构的分类算法，能够处理非常复杂的数据关系。神经网络通过多层非线性变换来学习数据的特征，适用于图像、语音等高维数据的分类。

5. K-近邻算法（KNN）

K-近邻算法是一种基于实例的学习方法，它通过计算测试样本与训练集中样本的距离，然后根据最近的K个训练样本的类别来预测测试样本的类别。KNN算法简单，但计算成本高，尤其在大数据集上。

6. 梯度提升树（GBT）

梯度提升树是一种迭代的增强算法，通过构建一系列弱分类器（通常是决策树），然后将它们组合成一个强分类器。GBT能够处理非线性关系和特征间的相互作用，同时具有较高的预测精度。

示例：使用SVM处理非线性数据

假设我们有一组非线性可分的数据，我们将使用Python的scikit-learn库中的SVM来处理这个问题。

# 导入必要的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载数据集
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]  # 只使用花瓣长度和宽度作为特征
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)

# 数据预处理
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

# 使用SVM进行分类
svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)

# 预测
y_pred = svm.predict(X_test_std)

# 计算准确率
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))

在这个例子中，我们使用了SVM的径向基函数（RBF）核来处理非线性数据。通过调整gamma和C参数，我们可以优化模型的性能。gamma控制了RBF核的宽度，而C是正则化参数，用于平衡模型的复杂度和过拟合的风险。

中的SVM来处理这个问题。

# 导入必要的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载数据集
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]  # 只使用花瓣长度和宽度作为特征
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)

# 数据预处理
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

# 使用SVM进行分类
svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)

# 预测
y_pred = svm.predict(X_test_std)

# 计算准确率
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))