【数学】如何解高次的方程

最近我发现一个问题，大家都特别爱解方程，但是一遇到高次的方程，就很难解出来，我想了一下，发现很多人的研究方向都是执着于找出一个根式解，即找出一个公式解，所以我想能不能放弃公式的办法，用分步的办法来解决。
考虑一个方程（1）：

这是一个拥有三个根的5次方程

这是它的表达式
我们要求它和x轴的交点横坐标
观察上图，不难注意到，方程的根一定存在于拐点和拐点之间或者拐点和正/负无穷的区间上，但这不意味着拐点和拐点之间或者拐点和正/负无穷的区间上一定有根
例如

既然能够确定根的范围，那么，就好办了
对方程（1）求导，得到方程（2），求其根，这是为了找出其中拐点的位置：


发现是一个4次方程，很不好求，但是依然符合我们刚才发现的规律，那么我们再次求导，得到方程（3）：


发现三次方程也不好求，那么再次求导得到方程（4）：


发现方便求根！所以求得两根：-0.4和0
这对应了方程（3）中拐点的横坐标，而这些拐点之间很有可能有我们想要的根，那么接下来，就要求得其根。考虑到在每一个区间内使用牛顿迭代法可能收敛在别的地方，并且区间内如果没有根的话会很浪费算力。所以，我们需要一种高效，准确，能够确定区间内有没有根的算法。先来看第一点：确定区间内的根，既然已经找出所有可疑的区间了，那么只要判断区间两端的函数值是否不同即可判断是否有根，如果不同则有根，反之亦然。
（方程（3））：

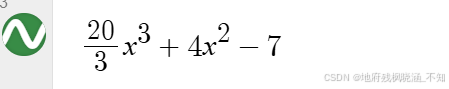
根据求得的结果，注意到三个可疑的区间：
[-inf,-0.4]，[-0.4,0]，[0,inf]
求得方程在负无穷处的极限为负无穷，在-0.4处的值为-6.78667，同号，无根
求得方程在-0.4的值为-6.78667，在0处的值为-7，同号，无根
求得方程在0出的值为-7，在正无穷处的极限为正无穷，异号，有根
那么已经找出了有根的区间，如何确定根的位置？
注意到我们可以注意到开区间内方程（函数）的走势为严格单调递增，并且可以应用牛顿迭代。如果能够获取区间内另一个异号点（异号的函数值点）的话则可以应用以下算法：
1.取区间中值，根据函数走势判断根在中值点左边还是右边
2.判断完成后再取新区间中值
3.重复，直到区间长度小于允许的误差范围，或者取到的中值接近于零，在可以容忍的误差范围内
应用此方法，求解出方程（3）的解为0.85074
这意味着对于方程（2），只有一个拐点，并且只有两个可疑的区间了

那么，对于区间[-inf,0.85074]和[0.85074,inf]检查根
函数在负无穷处的极限为正无穷，在拐点处为-9.26116
函数在正无穷处的极限为正无穷，在拐点处为-9.29116
都是异号，则有两个根
分别在(-inf,0.85074)和(0.85074,inf)区间内任取一点应用牛顿迭代或者注意到当x=2和x=-2时为正，则应用刚才的算法
最终求得两根：-0.72132和1.59394
那么，接下来，可以对方程1求根了

三个可疑的区间：
[-inf,-0.72312]，[-0.73212,1.59394]，[1.59394,inf]
开始检查：
lim x->-inf equation(x)=-inf , equation(-0.72312)=6.81096 ,true
equation(-0.72312)=6.81096 , equation(1.59394)=-6.28077 ,true
equation(1.59394)=-6.28077 , lim x->inf equation(x)=inf ,true
发现三个区间都有根，那么：
注意到x=-2，函数值为-4.3333…，那么对于[-2,-0.72312]应用区间中值算法
求得-1.79189
对于[-0.73212,1.59394]应用区间中值算法
求得0.69126
注意到x=3，函数值为66.5，那么应用区间中值算法
求得2.13196
至此，方程得解。
注：在无穷到某一值的区间内，可以应用牛顿迭代，但是考虑到并不是每个函数的走势都稳定，很有可能求出别的根。
总结：此方法通过应用介值定理判断根是否存在，利用了正整数次幂函数处处连续可导的特性，并通过高阶导数求根辅助低阶导数求根这种递进的方式求得最终的根，甚至可以对原方程积分，求出更高次方程的拐点和根。