【保姆级图解】选择排序 算法详解：直接选择排序、堆排序

引入

在计算机科学的算法领域中，排序是一项基础且重要的操作。它旨在将一组无序的数据元素重新排列为有序序列，以满足特定的顺序要求，如升序或降序。常见的排序算法可分为不同类别，像插入排序，包含直接插入排序和希尔排序；选择排序，有直接选择排序和堆排序；交换排序，涵盖冒泡排序和快速排序；还有归并排序 。这些算法各有特点，适用于不同的应用场景，接下来让我们深入了解它们。

选择排序引入

想象你面前有一堆杂乱无章的扑克牌，想要按照从大到小的顺序整理好。最直接的办法就是每次从这堆牌里挑出最大的一张，放在新牌堆的最前面，然后继续在剩下的牌里重复这个过程，直到所有牌都排好序。这就是选择排序的基本思路 —— 在待排序的数据中不断找出最值，放到合适的位置，就像整理扑克牌一样，用简单直接的方式让混乱的数据变得井井有条 。

一、直接选择排序

算法思想
直接选择排序的核心是每次从待排序序列中选出最小（或最大）元素，存放到已排序序列的末尾。在优化版本中，可以同时找出每轮的最小值和最大值，分别放到序列的两端，从而减少排序轮数。

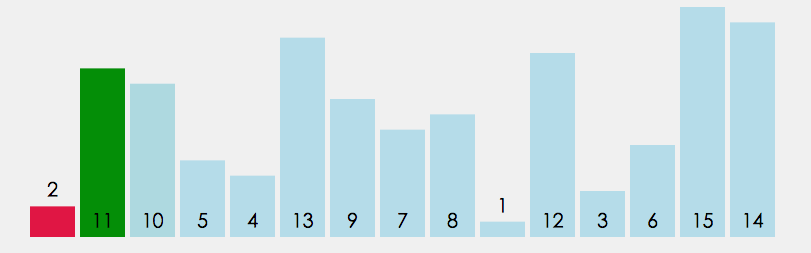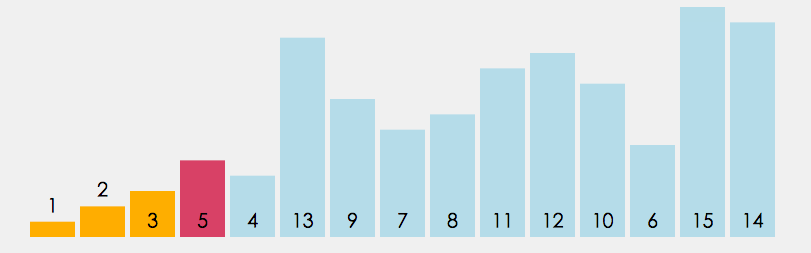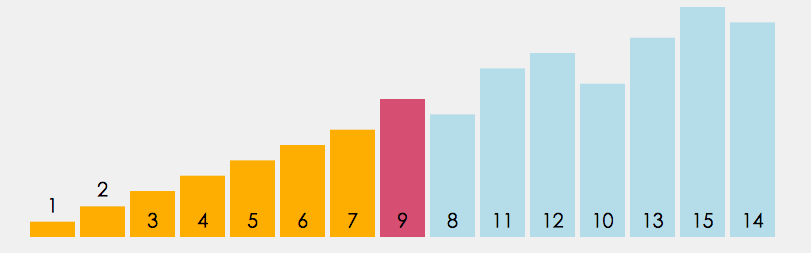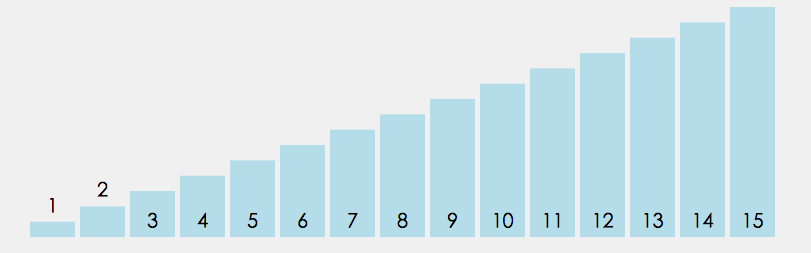
以下代码实现的是双找法，二个最值一起找(最大和最小)

void SelectSort(int* arr, int n) {
    int begin = 0, end = n - 1;
    while (begin < end) {
        int maxi = begin, mini = begin;
        // 遍历未排序区间，找到最大值和最小值的位置
        for (int i = begin + 1; i <= end; i++) {
            if (arr[i] < arr[mini]) mini = i;
            if (arr[i] > arr[maxi]) maxi = i;
        }
        // 若最大值在起始位置，需调整maxi指向
        if (begin == maxi) maxi = mini;
        swap(&arr[begin], &arr[mini]);  // 将最小值放到前面
        swap(&arr[end], &arr[maxi]);     // 将最大值放到后面
        begin++;
        end--;
    }
}

时间复杂度

• 无论数据是否有序，时间复杂度均为 O(n²)。每轮需要遍历剩余元素，共需约 n/2 轮。

优缺点

• 优点：实现简单，不需要额外空间。

• 缺点：不稳定，时间复杂度较高，适合小数据量。

---

二、堆排序

算法思想
堆排序基于二叉堆数据结构，通过构建最大堆（或最小堆），将堆顶元素（最大值）与末尾元素交换，并调整堆，重复此过程直至有序。

代码实现(堆详细讲法)

// 向下调整（维护大顶堆）
void AdjustDown(int* a, int n, int parent) {
    int child = parent * 2 + 1; // 左子节点
    while (child < n) {
        // 选择较大的子节点
        if (child + 1 < n && a[child] < a[child + 1]) child++;
        if (a[child] > a[parent]) {
            swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        } else break;
    }
}

// 堆排序
void HeapSort(int* a, int n) {
    // 从最后一个非叶子节点开始建堆
    for (int i = (n - 2) / 2; i >= 0; i--) AdjustDown(a, n, i);
    // 交换堆顶与末尾元素，逐步缩小堆范围
    int end = n - 1;
    while (end > 0) {
        swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        end--;
    }
}

时间复杂度

• 建堆过程：O(n)

• 排序过程：每次调整 O(logn)，共 O(n logn)

• 总体时间复杂度：O(n logn)

优缺点

• 优点：时间复杂度低，适合大数据量。

• 缺点：不稳定，数据跳跃式交换可能影响缓存效率。

---

四、二种算法对比

算法	平均时间复杂度	空间复杂度	稳定性	适用场景
直接选择排序	O(n²)	O(1)	不稳定	小数据量，简单实现
堆排序	O(n logn)	O(1)	不稳定	大数据量，内存有限

---

五、总结

• 直接选择排序：实现简单，但效率较低，适用于对稳定性无要求的小数据。

• 堆排序：高效的大数据排序算法，但存在不稳定性和缓存不友好问题。

实际应用中，需根据数据规模、有序性及稳定性需求选择合适的算法。例如，快速排序结合插入排序的混合方案（如 Introsort）能兼顾不同场景的效率。