滤波器设计
理想低通滤波器:
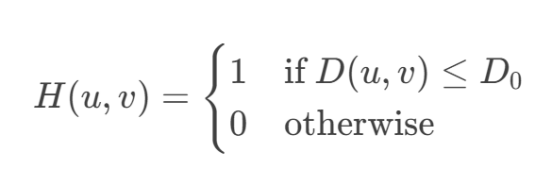
其中 D(u,v) 为频率点到中心的距离,D0为截止频率。
实验结果分析
- 滤波效果:
低频保留:平滑图像,去除高频噪声(如边缘细节)。
振铃效应:由于理想滤波器的陡峭截止,会在图像边缘产生伪影(Gibbs现象)。
- 不同截止频率比较:
D0较小:图像模糊严重(仅保留极低频)。
D0增大:更多细节保留,但振铃效应更明显。
%% 实验要求2:理想低通滤波
clc; clear; close all;
img = imread('cherry.jpg');
if size(img,3)==3
img = rgb2gray(img);
end
[M,N] = size(img);
f = fft2(double(img));
fshift = fftshift(f);
% 创建理想低通滤波器
D0 = 30; % 截止频率
[u,v] = meshgrid(1:N,1:M);
D = sqrt((u-N/2).^2 + (v-M/2).^2);
H = double(D <= D0);
% 滤波
filtered_fshift = fshift .* H;
filtered_f = ifftshift(filtered_fshift);
filtered_img = real(ifft2(filtered_f));
% 显示结果
figure;
subplot(1,3,1); imshow(img); title('原图像');
subplot(1,3,2); imshow(H); title('低通滤波器(D0=30)');
subplot(1,3,3); imshow(filtered_img,[]); title('滤波后图像');
% 不同截止频率比较
D0_values = [15, 30, 60];
figure;
for i = 1:length(D0_values)
D0 = D0_values(i);
H = double(D <= D0);
filtered_fshift = fshift .* H;
filtered_img = real(ifft2(ifftshift(filtered_fshift)));
subplot(1,3,i); imshow(filtered_img,[]);
title(['D0=',num2str(D0)]);
end结果如下:
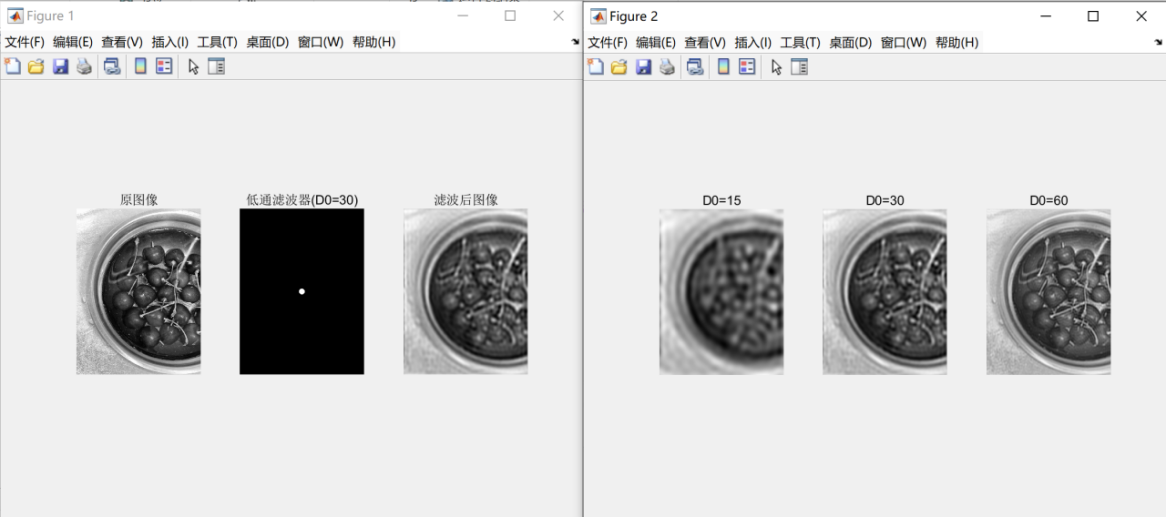
 理想低通滤波器设计与实验结果分析
理想低通滤波器设计与实验结果分析























 1981
1981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








