基于图像的三维重建——对极几何(3)

---

对极约束

如图所示，描述的是空间中的一点在左右两个相机中成像，空间点在两个相机的成像点通过外参矩阵R,t建立了一个等式关系，或者称为一种约束关系，这个约束就叫做对极约束。以下两式描述了两个像素坐标x₁ 和x₂的关系。

公式推导如下图：

基础矩阵F

基础矩阵性质

基础矩阵求解方法

基础矩阵的求解主要有两种方法：1.直接线性变换法；2. 基于RANSAC的鲁棒方法求得。

直接线性变换法

基于RANSAC的鲁棒方法

算法流程为：

1. 随机采样8对匹配点(x₁⁽ⁿ⁾ ,x₂⁽ⁿ⁾）；
2. 8点法求解基础矩阵$\hat{F}$;
3. 奇异值约束获取基础矩阵F；
4. 计算误差，并统计内点个数；
5. 重复上述过程，选择内点数最多的结果；
6. 对所有的内点执行2，3,重新计算F。

其中，采样次数计算满足下式：

内点判断标准满足下式：

本征矩阵E

本征矩阵性质

本征矩阵求解

从本征矩阵中恢复相机姿态

本质矩阵有良好的性质，它的奇异值是[σ,σ,0]的形式，可以通过SVD分解得到R和t。若E的SVD分解为E = U Σ V^T ,其中Σ = diag(σ,σ,0)，则R和t的可能结果如下：

其中

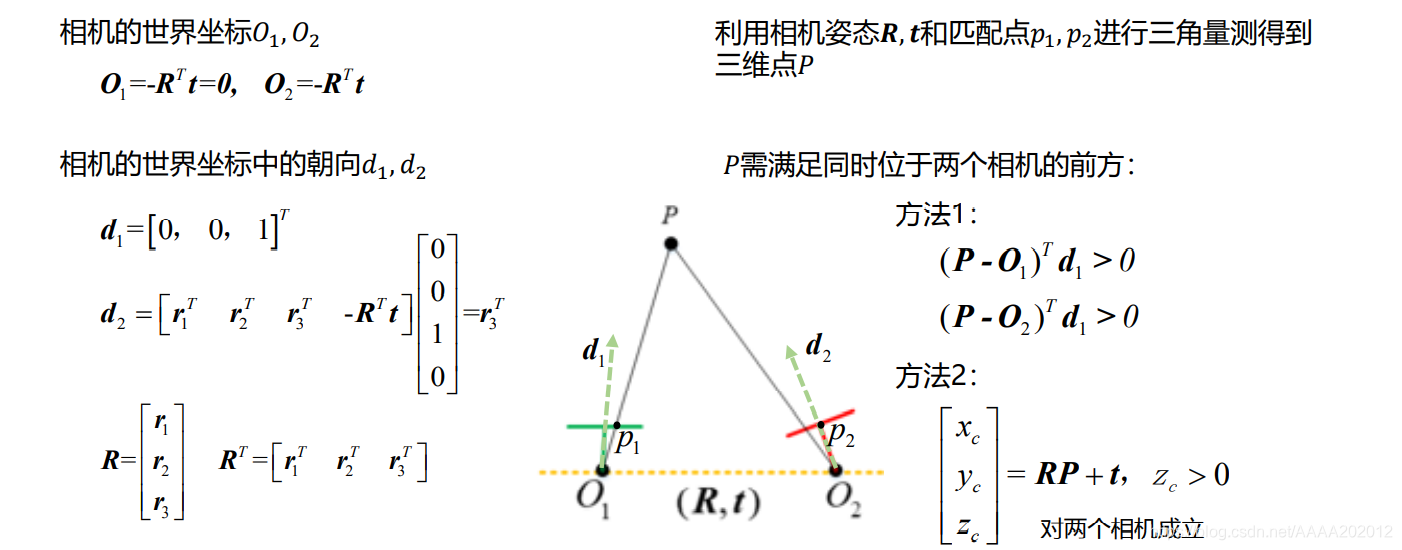
一共存在四组可能的R,t组合，如下图所示：

那么如何选择正确的相机姿态呢：需要让空间中一点同时位于两个相机的前方。

单应矩阵H

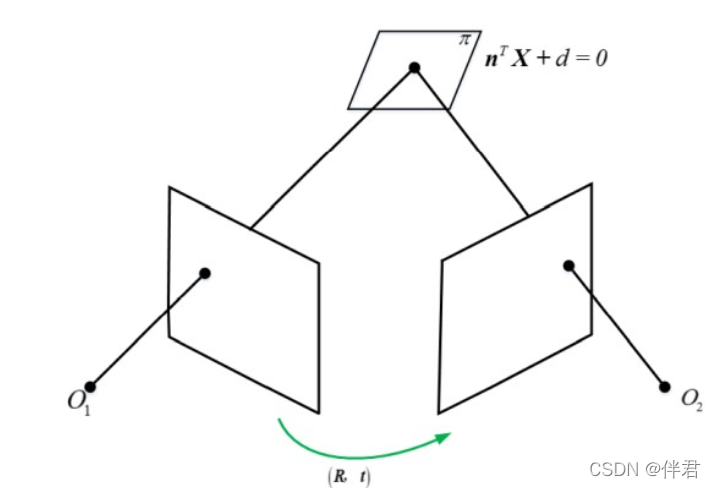
基础矩阵和本征矩阵是一种坐标之间的内在约束式，并不是两个像素之间的相互转换关系。而单应矩阵可以将不同相机对应点像素坐标进行转换，条件是当空间中特征点位于一平面上。如下图：

单应矩阵性质

单应矩阵求解

直接线性变换求解单应矩阵

RANSAC法估计单应矩阵

算法流程：

1. 随机采样4对匹配点(x₁⁽ⁿ⁾ ,x₂⁽ⁿ⁾）；
2. 4点法求解基础矩阵H;
3. 计算误差，并统计内点个数；
4. 重复上述过程，选择内点数最多的结果；
5. 对所有内点执行3，4，重新计算H

其中，内点判断标准为：