相对定向与绝对定向

连续相对定向与绝对定向：构建立体模型的步骤详解

原创已于 2022-04-15 11:00:39 修改 · 2.8w 阅读

99 ·

CC 4.0 BY-SA版权

文章标签：

#相对定向 #绝对定向 #摄影测量

于 2022-04-15 10:35:59 首次发布

摄影测量专栏收录该内容

5 篇文章

订阅专栏

1.相对定向

在这里介绍相对定向是为了下一步的核线影像生成，主要讲解连续法相对定向，需要同名点坐标（特征匹配算法即可得到）。

1.1理论知识

根据书上说的，确定一个立体像对两像片的相对位置称为相对定向。一般确定两像片相对位置有两种方法：其一是将摄影基线固定水平，称为独立像对相对定向系统；其二是将左像片置平或将其位置固定不变，称为连续像对相对定向系统。这两种系统选取了不同的像空间辅助坐标系，因为有不同的相对定向元素。

相对定向的原理是同名光线对对相交于核面内。(这里不作赘述)

1.1.1 连续像对的相对定向元素
若将左片置平，以左片的像空间坐标系作为本像对的像空间辅助坐标系(或称以左方像片为基准或左像片的外方位元素已知)，这样的像对为连续像对。如下图所示，S₁-X₁Y₁Z₁为本像对的像空间辅助坐标系，此时，S₁在该坐标系的坐标为：X_S1=Y_S1=Z_S1=0，像片的三个角元素亦为零，即 $ϕ\phi$ ₁= $ω\omega$ ₁= $κ\kappa$ ₁=0。而在右像片中，S₂在S₁-X₁Y₁Z₁坐标系的坐标为：X_S2=B_x，Y_S2=B_y，Z_S2=B_z，三个角元素为 $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂。其中,B_x，B_y，B_z也称为基线分量（模型上的）。在上述的六个元素B_x，B_y，B_z及 $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂中，因B_x只影响相对定向后建立模型的大小而并不影响模型的建立，因此，称B_y，B_z， $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂为连续相对定向的五个相对定向元素，只要恢复了立体像对这五个元素，就确定了像片对的相对位置，完成了相对定向，可建立与地面相似的几何模型。

1.1.2 单独像对相对定向元素
若将摄影基线置平，像空间辅助坐标系选取S₁为坐标原点，基线B作为X轴，垂直于左核面的轴为Y轴构成右手平面坐标系S₁-X₁Y₁Z₁，这样的像对为单独像对，如下图所示。此时对左像对，三个线元素为：X_S1=Y_S1=Z_S1=0，因左光轴在S₁-X₁Z₁平面内，三个角元素为： $ω\omega$ ₁=0， $ϕ\phi$ ₁， $κ\kappa$ ₁，对于右像片，三个线元素为：X_S2=B_x=B,Y_S2=0,Z_S2=0;三个角元素为 $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂。上述的六个元素B、 $ϕ\phi$ ₁， $κ\kappa$ ₁， $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂中，B只涉及模型的比例尺，即影响模型的大小而不影响重建模型，因此，称 $ϕ\phi$ ₁， $κ\kappa$ ₁， $ϕ\phi$ ₂， $ω\omega$ ₂， $κ\kappa$ ₂为单独像对的相对定向五个元素。

1.2 编程实现

//代码都写在了机房的电脑上，最近疫情机房不让去，稍后补上。

2.绝对定向

相对定向仅仅是恢复了摄影时像片之间的相对位置，所建立的立体模型是一个以相对定向选定得像空间辅助坐标系为基准得模型。还要把模型点在像空间辅助坐标系中的坐标转化为地面摄影测量坐标(X,Y,Z)

2.1理论知识

绝对定向就是借助已知的地面控制点确定立体模型比例尺和地面坐标系中所处方位的过程。原理是将相对定向好的模型进行旋转和平移，使它与地面量测的数据相匹配，从而在模型中建立起地面坐标系统。

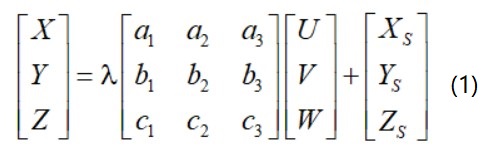
该式为绝对定向的基本关系式。由于这种变换前后图形的几何形状相似，所以又称为空间相似变换。式中，(X,Y,Z)为模型点的地面摄影测量坐标，(U,V,W)为同一模型点在像空间辅助坐标系的坐标。 $λ\lambda$ 为模型缩放比例因子，(a₁,a₂,…c₃)为两个坐标轴三个转角 $Φ\Phi$ 、 $Ω\Omega$ 、K计算出来的方向余弦，(X_S,Y_S,Z_S)为坐标原点的平移量，称七个参数X_S,Y_S,Z_S， $λ\lambda$ ， $Φ\Phi$ 、 $Ω\Omega$ 、K为模型的绝对定向参数，即确定相对定向所建立的模型空间方位的元素。绝对定向的任务就是借助地面控制点，恢复或计算这七个元素，这也是解析法绝对定向的定义。

2.1.1 绝对定向公式的线性化及绝对定向元素的解算
利用地面控制点解求绝对定向元素时，控制点的地面摄影测量坐标(X,Y,Z)均为已知值，模型的像空间辅助坐标(U,V,W)为计算值，式中只有七个绝对定向元素是未知数。因此绝对定向公式是一个多元非线性函数，使其线性化，引入七个绝对定向元素的初始值及改正值：

将(2)式代入(1)，按泰勒级数展开，取一次项得：

在考虑小角的情况下，(1)式的近似式可表示为：

对上式微分后代入(3)式，取小值一次项得：

上式中含有七个未知数，需要列七个方程，因此，至少需要两个平高点和一个高程点，而且三个控制点不能在一条直线上。生产中，一般是在模型四个角布设四个控制点。当有多余观测时，应按最小二乘法解求，将上式中模型的像空间辅助坐标(U,V,W)视为观测值，其改正数为v_u,v_v,v_w,写成误差方程形式，得：

式中，

2.1.2 坐标重心化
实际计算绝对定向元素时，常选模型的重心为坐标原点将坐标重心化，这种数据处理方法的好处是：可以减少模型点坐标在计算过程中的有效位数，以保证计算精度；可以使法方程系数简化，个别项的数值变为零，部分未知数可以分开求解，从而提高了计算速度。

单元模型中全部控制点的空间辅助坐标和地面摄影坐标的重心坐标为：

相应的重心化坐标为：

将重心化坐标带入绝对定向的基本公式，得：

由此得到用重心化坐标表示的误差方程式为：

式中，

2.1.3 绝对定向的解算流程
绝对定向的具体解算过程归纳为：
1.确定待定参数的初始值， $Φ\Phi$ ⁰ = $Ω\Omega$ ⁰ = K⁰ = 0, $λ\lambda$ ⁰ = 1, $Δ\Delta$ X = $Δ\Delta$ Y = $Δ\Delta$ Z = 0;
2. 计算控制点的地面摄影测量坐标系重心的坐标和重心化坐标；
3. 计算控制点的空间辅助坐标重心坐标和重心化坐标；
4. 计算常数项；
5. 按下式计算误差方程系数；

6. 逐点法化及法方程求解；
7. 计算待定参数的新值：

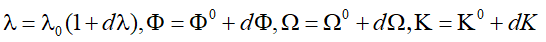
8.判断d $Φ\Phi$ 、d $Ω\Omega$ 、dK是否小于给定的限值。若大于限值，将求得的所有未知参数的改正数加到近似值作为新的近似值作为新的近似值，重复上述计算问题，逐步趋近，直到满足要求。

求出绝对定向元素之后，可根据待求点的重心化坐标( $U‾\overline{U}$ , $V‾\overline{V}$ , $W‾\overline{W}$ )按(9)式求出待求点的重心化地面摄影测量坐标( $X‾\overline{X}$ , $Y‾\overline{Y}$ , $Z‾\overline{Z}$ )，再加上重心坐标(X_g,Y_g,Z_g)后得待求点的地面摄影测量坐标(X,Y,Z)，最后将地面摄影测量坐标再转回到地面测量坐标，提交成果。(应注意，绝对定向是像空间辅助坐标(U,V,W)和地面摄影测量坐标(X,Y,Z)间的变换。因地面摄影测量坐标系的原点再测区内某点，其三轴系的选取几乎与像空间辅助坐标系平行，所以两坐标轴旋转时，K是个小角值，这便于计算。但提供绝对定向用的地面控制点为地面坐标(X_t,Y_t,Z_t)，所以，在进行绝对定向前，还要将地面测量坐标(X_t,Y_t,Z_t)转换为地面摄影测量坐标(X,Y,Z)。)

2.2 编程实现

//代码都写在了机房的电脑上，最近疫情机房不让去，稍后补上。

3.双像解析的相对定向-绝对定向法

立体像对相对定向-绝对定向法解求模型点的地面坐标，其过程为：
1.用连续像对或单独像对的相对定向元素的误差方程式解求像对的相对定向元素；
2.由相对定向元素组成左、右像片的旋转矩阵R₁,R₂,并利用前方交会式求出模型点在像空间辅助坐标系中的坐标；
3.根据已知地面控制点的坐标，按绝对定向元素的误差方程式解求该立体模型的绝对定向元素；
4.按绝对定向公式，将所有待定点的坐标纳入到地面摄影测量坐标系中。