今天谈论的重点是数值稳定性,在计算机编程中,有很多算法都需要考虑数值稳定性。比如在机器学习算法中我学过的Logistic回归的牛顿迭代解法,在牛顿迭代时需要解线性方程组,由于Hessian矩阵是对称正定的,用Cholesky矩阵分解不但可以大大减少运算量,而且还具有很好的数值稳定性。借此机会来更多地了解一下数值稳定性。
在计算机编程中,有时候同一个计算问题,不同算法中舍入误差对计算的结果产生的影响各不相同,舍入误差对计算结果的精确度影响小的算法,具有较好的数值稳定性;反之,算法的数值稳定性差。所设计的算法的舍入误差在一定条件下要能够控制。否则就像蝴蝶效应一样,使风和日丽的美洲几个月后出现狂风暴雨。
接下来我们先来看一个比较经典的例子。
题目:计算如下积分的值
分析:很容易,可以进行如下推导过程
根据这个递推式,可以计算任意的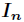
可以看出误差是逐渐放大的,在一定范围内无法控制,这样做的结果就是最终答案与真实答案相差十万八千里。
为了提高数值的稳定性,我们在设计算法时需要遵循如下几个原则
(1)尽量减少运算次数
(2)加法运算时,避免大数加小数
(3)避免两个相近数相减
(4)避免小数做除数或大数做乘数
(1)尽量减少运算次数
比如计算多项式的秦九韶算法,再比如下例
题目:计算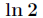
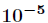
分析:用两种方法进行比较,以此说明运算次数的重要性。首先采用如下公式计算
即得到
要精确到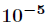
这样的话取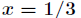
要精确到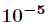
可以看出第二种方式大大减少了计算量,精度相应也会损失很少。
(2)加法运算时,避免大数加小数
针对浮点数来说,由于有效数字的保留问题,大数会“吃掉”小数。
(3)避免两个相近数相减
比如在二次方程求根问题中,解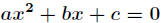

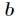

其中有两个相近的数相减,这会导致误差增大,但是考虑另一种方法,先计算出
然后再根据
计算得到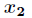
(4)避免小数做除数或大数做乘数
高斯消元中,选主元与不选主元计算得到的结果有差异,因为如果不选主元可能遇到小数做除数的情况。从
而导致结果出现偏差。
推荐文章:http://www.cyqdata.com/cnblogs/article-detail-35278








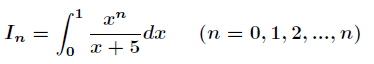
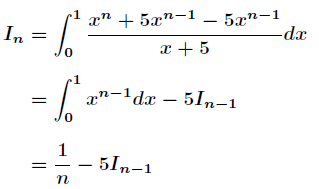
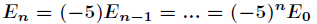
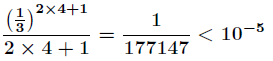
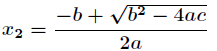
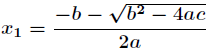
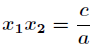
















 4525
4525

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








