常用信号去噪与回归方法的原理及MATLAB实现
一、应用背景
“信号去噪”与“信号回归”是信号处理的基本技术。本博客针对一类特殊的问题(峰值缓变函数优化),对这两类技术展开讨论。
峰值缓变函数是指最值附近的函数值变化十分平稳,当存在噪声干扰时,会导致优化算法的性能十分不稳定。因此,对于这类函数(信号)为了充分发挥优化算法的性能,可在前期进行“去噪”或“回归”处理。
例如:
f ( x ) = 1 1 + ( x − 1 ) 6 + 0.02 x f\left( x \right) = \frac{1}{
{1 + {
{\left( {x - 1} \right)}^6}{\text{ + }}0.02x}} f(x)=1+(x−1)6 + 0.02x1
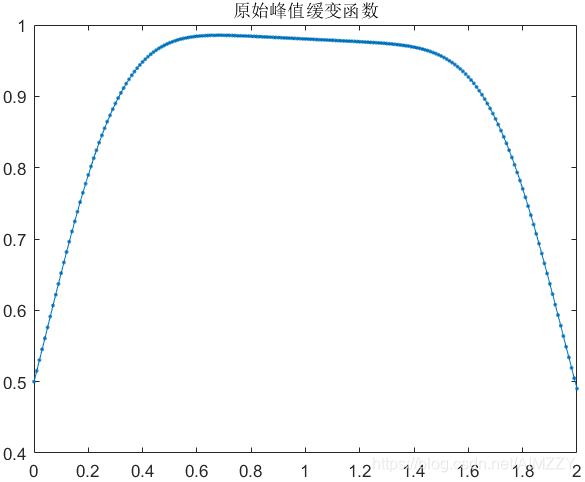
该函数(信号)及其加噪后的最优解如下所示:
| 原始信号 | 加噪后信号( σ 2 σ^{2} σ2 =0.02) |
|---|---|
 |
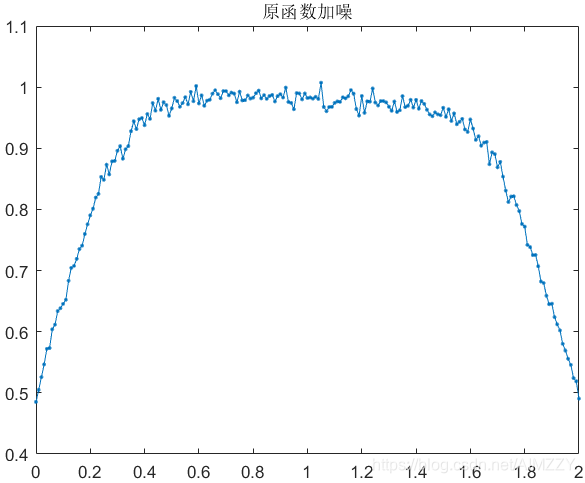 |
| x o p t x_{opt} xopt=0.68 | x o p t x_{opt} xopt=1.05 |
接下来,便针对如何从含噪信号最大程度恢复最优解展开讨论与实验。
二、信号去噪
1、低通滤波去噪
由于目标函数在峰值附近的缓变的,故峰值附近的频谱以低频分量为主;而噪声往往分布在高频区域。故直接进行低通滤波可在一定程度上实现去噪,而几乎不会改变峰值的特性。
| 原始信号 | 含噪信号 | 去噪信号 | |
|---|---|---|---|
| 信号 | 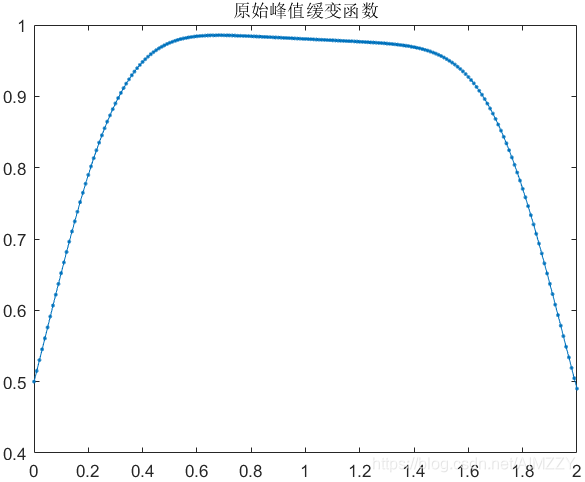 |
 |
 |
| 频谱 |  |
 |
 |
| 最优解 | x o p t x_{opt} xopt=0.68 | x o p t x_{opt} xopt=1.05 | x o p t x_{opt} xopt=0.66 |
2、小波分解去噪
2.1 Mallat金字塔算法
Mallat金字塔算法,利用“双尺度关系”,为小波变换赋予了“多分辨率表示”的物理意义。内层分解表示信号的基本(大尺度)信息,而越往外层,分解提供越细节(小尺度)的信息。
![(img-qe2s7eOo-1590065046978)(en-resource://database/10764:1)]@w=600](https://i-blog.csdnimg.cn/blog_migrate/d4d08c72de2145acfcbe779a02c6ceb5.png)
2.2 小波基的选取
2.2.1 小波基的种类

MATLAB小波基函数(MathWorks)
MATLAB中的小波基介绍(CSDN)
2.2.2 小波基的选取原则
① 正交性
② 支撑区间
支撑区间长度是指随 时间/频率 趋于 ∞ 时,小波函数收敛到零所需的长度。
“紧支撑”是指对于函数 f(x),如果自变量 x 在 0 附近的取值范围内,f(x) 能取到值;而在此之外,f(x) 取值为 0,那么这个函数 f(x) 就是紧支撑函数,而这个 0 附近的取值范围就叫做紧支撑集。总结为一句话就是“除在一个很小的区域外,函数取值为零,即函数有速降性”。
③ 对称性
对称性使小波具有线性相移,这对于图像处理具有重要意义。
④ 正则性
正则性描述小波基函数的平滑程度
2.3 小波分解去噪仿真
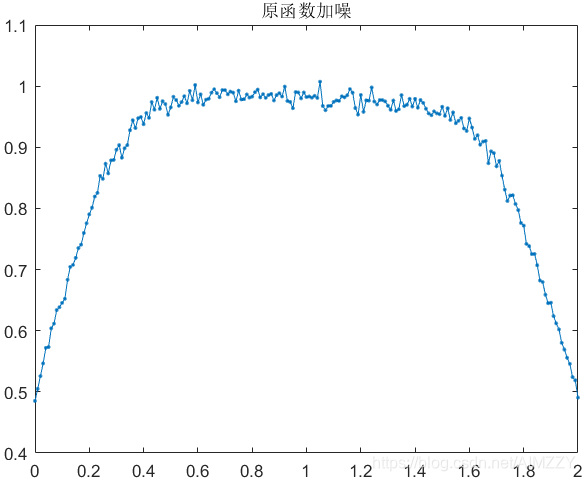
这里选取 7 层小波分解,内3层利用软阈值(0.014)处理,外4层利用硬阈值置0;
| 原始信号 | 含噪信号 | 去噪信号 | |
|---|---|---|---|
| 信号 |  |
 |
 |
| 最优解 | x o p t = 0.68 x_{opt}=0.68 xopt=0.68 | x o p t = 1.05 x_{opt}=1.05 xopt=1.05 | x o p t = 0.71 x_{opt}=0.71 xopt=0.71 |
3、奇异值分解去噪
3.1 信号奇异值分解去噪原理
前面所述的傅里叶变换与小波变换,都是从信号能量入手,通过对信号进行某种分解,实现去噪。
而借助奇异值分解(SVD)我们可以从信号结构层面进行去噪。然而,奇异值分解是针对矩阵的,这里待去噪信号仅有一个一维信号,故我们首先需要构造信号的重构矩阵。
3.1.1 信号的矩阵重构
对于信号 y ( i ) , i = 1 , 2 , . . . , N y(i) , i=1,2,...,N y(i),i=1,2,...,N,基于相空间重构理论,可以由其构造重构矩阵 A A A
[ y ( 1 ) y ( 2 ) ⋯ y ( N − L + 1 ) y ( 2 ) y ( 3 ) ⋯ y ( N − L + 2 ) ⋮ ⋮ ⋱ ⋮ y ( L ) y ( L + 1 ) ⋯ y ( N ) ] \begin{bmatrix} y(1) & y(2) & \cdots & y(N-L+1) \\ y(2) & y(3) & \cdots & y(N-L+2) \\ \vdots & \vdots & \ddots & \vdots \\ y(L) & y(L+1) & \cdots & y(N) \\ \end{bmatrix} ⎣⎢⎢⎢⎡y(1)y(2)⋮y(L)y(2)y(3)⋮y(L+1)⋯⋯⋱⋯y(N−L+1)y(N−L+2)⋮y(N)⎦⎥⎥⎥⎤
其中,不同的 L 选取,对应着不同尺寸的重构矩阵,一般 L 取为信号长度的一半。








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6598
6598

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








