利用矩阵能完成旋转。对于图中的点S(j,0),可以看作矩阵A[j,0],令点S旋转a度得到点T(m,n),可以看作矩阵C[m,n],显然可以存在变换矩阵B,令A×B=C成立。由简单的几何知识就能得出变换矩阵B的构造。
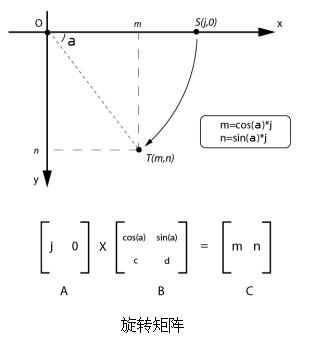
因为点S位于坐标轴上,使得计算矩阵B的过程极大的简化了。如果要对于位置不在坐标轴上的点进行旋转,其数学计算要复杂一些,其推导已经超出了本书的内容范围。不过最终确实可以证明,对于坐标空间中的任意点(x,y)经过旋转s度得到的点(m,n),存在以下公式:
m=a×cos(s)-b×sin(s)
n=a×sin(s)+b×cos(s)
于是可以得到通用的旋转变换矩阵如图所示:
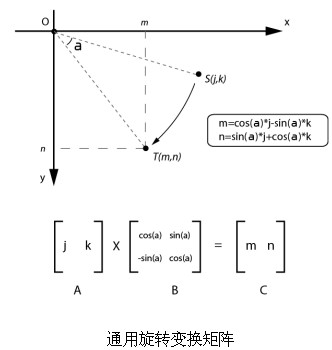
显然,这个通用矩阵对于坐标轴上的点也是适用的。
在AS3中使用变换矩阵操作显示对象时,总是套用显示对象上一级容器的坐标系。如果显示对象直接处在舞台根级别上,则坐标系原点就是舞台的左上角。





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








