强化学习基础知识笔记[5] - 值函数逼近

参考资料
[1] 强化学习入门 第五讲 值函数逼近
本文主要是对该资料学习的笔记，并且加入了一些自己的想法，如有错误欢迎指出。

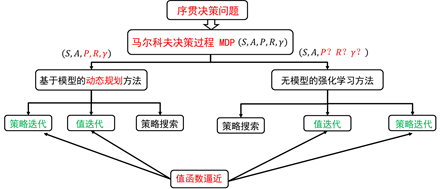
强化学习的分类

无模型强化学习 - 理论

强化学习的核心问题

强化学习的核心问题为：

1. 策略评估部分：值函数、状态-行为值函数的估计问题！
2. 策略改善部分：给定值函数下，$\pi (a|s)$的选取问题！

回报函数、值函数定义

累计回报函数
$$G_t=R_{t+1}+\gamma R_{t+2}+...=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\text{\hspace{1em}(1.1)}$$
状态值函数
$$v_{\pi }(s)=E_{\pi }[G_t]=E_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s\right]\text{\hspace{1em}(1.2)}$$
行为值函数
$$q_{\pi }(s,a)=E_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a\right]\text{\hspace{1em}(1.3)}$$
状态值函数和行为值函数的定义是在策略$\pi$下各次实现中累计回报函数的数学期望。

动态规划方法值函数：
$$V(s_t)=\sum _{a\in A}\pi (a|s)\left(R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^{a}V(s^{\prime })\right)\text{\hspace{1em}(1.4)}$$
动态规划方法值函数的计算用到了后继状态的值函数，利用bootstrapping方法，即用后继状态的值函数估计当前值函数。此时期望值由模型提供。

蒙特卡罗方法值函数：
$$V(s_t)=V(s_t)+\alpha (G_t-V(s_t))\text{\hspace{1em}(1.5)}$$
蒙特卡罗方法利用经验平均估计状态的值函数，即利用多次历史实验中该状态的平均累计回报函数来逼近期望。

时间差分方法值函数：
$$V(S_t)\leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))\text{\hspace{1em}(1.6)}$$

值函数逼近

之前介绍方法都是基于表格的强化学习，其维数为状态的个数，算法更新的是表格中具体状态下值函数的值。
在状态空间很大或者状态连续时无法使用网格进行表示，此时需要用到值函数逼近的方法逼近值函数。
本节中学习的是参数化值函数逼近。
其中参数化的意思是：

• 在线性逼近时值函数由一组函数（基函数）和一组参数组成，记为$v(s,\theta )$，更新的过程为更新参数向量$\theta$的值；
• 在非线性逼近时值函数一般由神经网络表示。

值函数的形式

首先在此给出线性逼近时的基函数表达式，这样后面看问题更加具体。
常用的基函数组：

• 多项式基函数
  $$(1,s_1,s_2,s_1^2,s_2^2,\cdots )$$
• 傅里叶基函数
  $${\varphi }_i(s)=cos(i\pi s),s\in [0,1]$$
• 径向基函数
  $${\varphi }_i(s)=exp(-\frac{||s-c_i|{|}^2}{2{\delta }_i^2})$$

此时值函数的表达式为：
$$\hat{v}(s,\theta )={\theta }^T\varphi (s)\text{\hspace{1em}(2)}$$

其中：

• ${\theta }^T$为参数向量，n维
• $\varphi (s)$为基函数组，n维

逼近过程

值函数的逼近是一个监督学习的过程，其输入数据为$s_t$，即当前的状态；相应的标签为$U_t$。其中，$U_t$在蒙特卡罗方法中为$G_t$，在时间差分法中为$r+\gamma Q(s^{{}^{\prime }},a^{{}^{\prime }})$，在TD(λ)中为$G_t^{\lambda }$
训练目标为：
$$argmi{n}_{\theta }(q(s,a)-\hat{q}(s,a,\theta ){)}^2\text{\hspace{1em}(3)}$$

需要说明的是，不同于表格型强化学习只更新当前状态$s_t$处的值函数，值函数逼近法在更新参数时会导致所有状态下值函数的改变！

值函数具体的更新方法有增量式学习和批方法。

增量式学习：随机梯度下降

在该方法下的参数随机梯度更新公式为：
$${\theta }_{t+1}={\theta }_t+\alpha [U_t-\hat{v}(s_t,{\theta }_t)]{\nabla }_{\theta }\hat{v}(s_t,\theta )\text{\hspace{1em}(3.1)}$$

其中：

• ${\theta }_{t+1}$、${\theta }_t$均为n维向量；
• ${\nabla }_{\theta }\hat{v}(s_t,\theta )$为对$\hat{v}(s_t,\theta )$求关于$\theta$的梯度，此时$s_t$为确定值；
• $\alpha$为学习率，需要设定较小的值。

关于$\alpha$较小取值的解释：逼近的值函数并不需要在各状态下都能达到最精确的值，而是要在整体上平衡所有不同状态的误差，因此需要较小的值。

对于蒙特卡罗方法，需要按照策略产生多组数据（从起始状态到最终状态的完整过程）,然后根据各组数据迭代更新值函数参数。假设一组数据为$<s_1,G_1>,<s_2,G_2>,<s_3,G_3>\dots$，此时需要按照下述公式更新值函数：
$$\Delta \theta =\alpha (G_t-\hat{v}(s_t,\theta )){\nabla }_{\theta }\hat{v}(s_t,\theta )\text{\hspace{1em}(3.2)}$$

算法描述为：

对于时间差分法，由于TD(0)方法中$U_t=R_{t+1}+\gamma \hat{v}(s_{t+1},\theta )$，目标值函数与估计的值函数均含θ。如果只考虑估计的值函数中θ，则该方法为半梯度法。此时的θ更新公式为：
$${\theta }_{t+1}={\theta }_t+\alpha [R+\gamma \hat{v}(s_{t+1},\theta )-\hat{v}(s_t,{\theta }_t)]{\nabla }_{\theta }\hat{v}(s_t,\theta ))\text{\hspace{1em}(3.3)}$$

基于半梯度的TD(0)算法描述为：

疑问：

• 公式3.3的中间出现了$\theta$。但没明确说明这是哪个时刻的。我的理解是${\theta }_t$，因为计算完${\theta }_{t+1}$之前只能使用旧值。

基于半梯度的Sarsa算法描述为：

总结一下几种方法的θ更新公式：

批方法

批的方法计算复杂，效率更高。